Numerical Examples

vel,q
Figure 1. BP gas-cloud model. (a) A portion of the BP 2004 velocity model; (b) the corresponding quality factor $Q$ model.

shots
Figure 2. Prestack data with attenuation. A total of $31$ shots were modeled.

cref,imgd,imgc
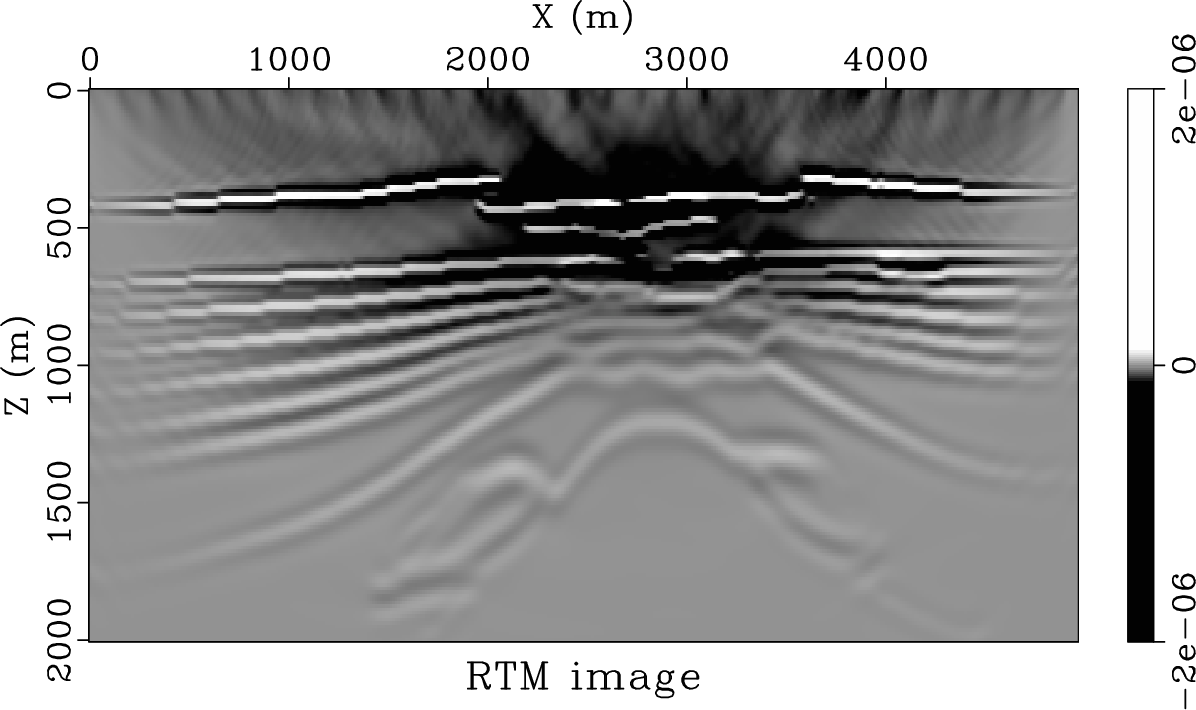
Figure 3. (a) The true reflectivity model; (b) image obtained by dispersion-only RTM without compensating for amplitude; (c) image obtained by $Q$-RTM. Note that no Laplacian filter is applied, and the color scales for RTM and $Q$-RTM images are different from that of the true model.

img-n-5,img-n-15,img-n-30
Figure 4. The results of the original LSRTM through iterations. (a) after $5$ iterations; (b) after $15$ iterations; (c) after $30$ iterations.

img-v-5,img-v-15,img-v-30
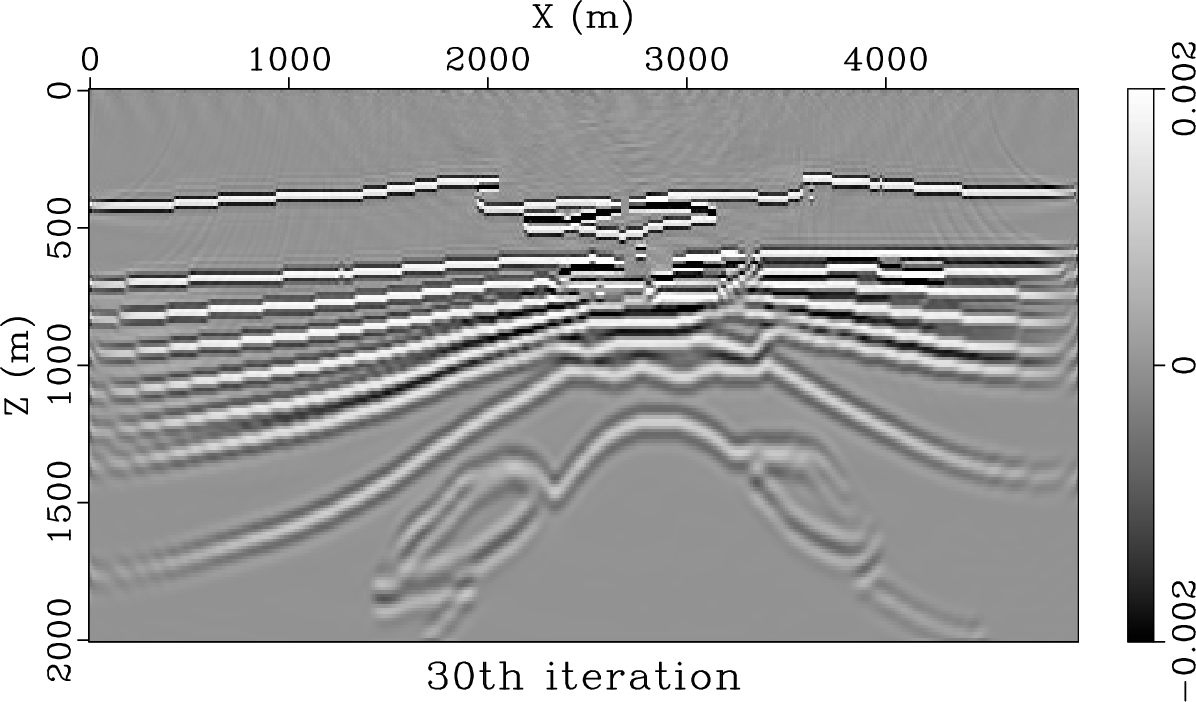
Figure 5. The results of the LSRTM with Laplacian filter through iterations. (a) after $5$ iterations; (b) after $15$ iterations; (c) after $30$ iterations.

img-c-5,img-c-15,img-c-30
Figure 6. The result of the proposed $Q$-LSRTM through iterations. (a) after $5$ iterations; (b) after $15$ iterations; (c) after $30$ iterations.

compare-n,compare-v,compare-c
Figure 7. Image traces extracted at $X=2500\;m$ from the $30$th iteration results (represented by the blue dashed line) compared with the true model (red solid line). (a) LSRTM; (b) LSRTM with the Laplacian filter; (c) $Q$-LSRTM.

conv
Figure 8. Convergence curves calculated by the $L_2$ norm of model misfit. The dot-dashed line corresponds to the original LSRTM, the dashed line corresponds to LSRTM with a Laplacian filter and the solid line corresponds to the proposed $Q$-LSRTM.

To test the convergence rate of $Q$-LSRTM, we use a portion of the BP 2004 velocity model (Billette and Brandsberg-Dahl, 2004) and the corresponding $Q$ model suggested by Zhu et al. (2014) (Figure 1). The model features a low-velocity, low-$Q$ area which is assumed to be caused by the presence of a gas chimney. The model has a spatial sampling rate of $12.5\;m$ along both vertical and horizontal directions. A total of $31$ shots with a spacing of $162.5\;m$ have been modeled with attenuation, and the source is a Ricker wavelet with $22.5\;Hz$ peak frequency (Figure 2). Performing RTM without compensating for amplitude loss, i.e. using the dispersion-only operator, leads to an image corresponding to Figure 3b, which suffers from poor illumination below the gas chimney. In contrast, $Q$-RTM appears capable of recovering the amplitude at deeper reflectors (Figure 3c), but the image still exhibits some differences from the true reflectivity. Note that the dispersion-only RTM image and $Q$-RTM image have the same phase but differ in amplitude. Next, we perform LSRTM (equation 19) and $Q$-LSRTM (equation 23) through a number of iterations. To test the separate effect of applying a Laplacian filter without compensating for attenuation, we also perform LSRTM with a Laplacian operator that removes low frequency artifacts. For fairness of comparison, all three methods are driven by the GMRES method, and because the tested model is small enough, they were not run in a restarted fashion. Using the original LSRTM (Figure 4), the inversion process attempts to remove low frequency noise and improve the illumination of deeper reflectors. However, at $30$th iteration, the reflector amplitude and sharpness beneath the attenuating area still have not been recovered. LSRTM with a Laplacian filter (Figure 5) achieves a somewhat sharper image, but because a Laplacian filter boosts high frequency components in the image, the reflectors beneath the attenuating zone remain poorly illuminated. In contrast, the proposed $Q$-LSRTM method (Figure 6) produces sharper reflectors with well-balanced illumination, especially in the area beneath the gas chimney using the same number of iterations. Note that the color scales used in all the three cases are kept the same as that of the true model (Figure 3a). Figure 7 compares the image traces extracted at $X=2500\;m$ from the $30$th iteration results against the true model. Clearly, the result obtained by the proposed $Q$-LSRTM best represents the true reflectivity, especially at deeper parts beneath the gas chimney (below $800\;m$ depth).

To measure the convergence rate, we calculate the model residual as the $L_2$ norm of the misfit between the model calculated at each iteration $\mathbf{m}_k$ and the true model $\mathbf{m}^*$, normalized by the $L_2$ norm of the true model:

$$r = {\frac{\Vert\mathbf{m}_k - \mathbf{m}^* \Vert^2_2}{\Vert\mathbf{m}^*\Vert^2_2}} \; .$$ (26)

Figure 8 shows the comparison of convergence rates. With the help of a Laplacian filter, LSRTM is able to achieve a slightly faster convergence rate at early iterations than the original LSRTM. The proposed $Q$-LSRTM, on the other hand, converges significantly faster than the other two methods. Convergence is achieved by $Q$-LSRTM within approximately $50$ iterations, while the other two methods have not converged even after $100$ iterations. The fast convergence is an important property, because for large-scale 3D seismic imaging problems only a few iterations can be afforded in practice.