Next: Bibliography Up: Li & Fomel: Time-to-depth Previous: Appendix C: Analytical expressions

Appendix D: Analytical expressions for the constant horizontal slowness-squared gradient medium

In this appendix, we study the following medium:

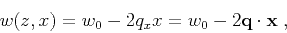$\begin{displaymath} w (z,x) = w_0 - 2 q_x x = w_0 - 2 \mathbf{q} \cdot \mathbf{x}\;, \end{displaymath}$

(55)

where $\mathbf{q} = [0,q_x]^T$ .

Similarly to the constant velocity gradient medium, it is convenient to write down the ray-tracing system in the form (Cervený, 2001)

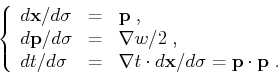$\begin{displaymath} \left\{ \begin{array}{lcl} d \mathbf{x} / d \sigma & = & \ma... ... d \sigma = \mathbf{p} \cdot \mathbf{p}\;. \end{array} \right. \end{displaymath}$

(56)

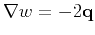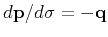Given equation D-1, $\nabla w = -2 \mathbf{q}$ and thus $d \mathbf{p} / d \sigma = - \mathbf{q}$ . After integration over $\sigma$ , equation D-2 becomes

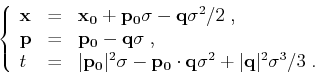$\begin{displaymath} \left\{ \begin{array}{lcl} \mathbf{x} & = & \mathbf{x_0} + \... ...2 + \vert \mathbf{q} \vert^2 \sigma^3/3\;. \end{array} \right. \end{displaymath}$

(57)

For a particular image ray

$\begin{displaymath} \left\{ \begin{array}{lcl} \mathbf{x_0} & = & [0, x_0]^T\;, ... ...0 - 2 q_x x_0}, 0]^T\;, \\ t_0 & = & t\;, \end{array} \right. \end{displaymath}$

(58)

the equation for 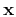$\mathbf{x}$ in D-3 simplifies to

$\begin{displaymath} \left\{ \begin{array}{lcl} x = x_0 - q_x \sigma^2/2\;, \\ z = \sigma \sqrt{w_0 - 2 q_x x_0}\;. \end{array} \right. \end{displaymath}$

(59)

Solving equation D-5 for $\sigma$ as a function of

and

$\begin{displaymath} \sigma (z,x) = \left[ \frac{(w_0 - 2 q_x x) - \sqrt{(w_0 - 2 q_x x)^2 - 4 q_x^2 z^2}}{2 q_x^2} \right]^{\frac{1}{2}}\;. \end{displaymath}$

(60)

Combining equations D-3 through D-6, we find

$\displaystyle x_0 (z,x)$	$\textstyle =$	$\displaystyle x + \frac{1}{2} q_x \sigma^2$
	$\textstyle =$	$\displaystyle \frac{2 w_0 x + q_x z^2}{w_0 + 2 q_x x + \sqrt{(w_0 - 2 q_x x)^2 - 4 q_x^2 z^2}}\;,$	(61)

$\displaystyle t_0 (z,x)$	$\textstyle =$	$\displaystyle (w_0 - 2 q_x x_0) \sigma + \frac{1}{3} q_x^2 \sigma^3$
	$\textstyle =$	$\displaystyle \frac{\sqrt{2} z \left[ 2 w_0 - 4 q_x x + \sqrt{(w_0 - 2 q_x x)^2... ..._0 - 2 q_x x + \sqrt{(w_0 - 2 q_x x)^2 - 4 q_x^2 z^2} \right]^{\frac{1}{2}}}\;.$	(62)

According to equation 4, D-7 can give rise to the geometrical spreading:

$\begin{displaymath} Q^2 (z,x) = \frac{2 [(w_0 - 2 q_x x)^2 - 4 q_x^2 z^2]} {(w_0... ...- 2 q_x x + \sqrt{(w_0 - 2 q_x x)^2 - 4 q_x^2 z^2} \right]}\;. \end{displaymath}$

(63)

It is more convenient to express equations D-1 and D-9 in $\sigma$ and

instead of directly in

and

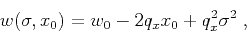$\begin{displaymath} w (\sigma,x_0) = w_0 - 2 q_x x_0 + q_x^2 \sigma^2\;, \end{displaymath}$

(64)

$\begin{displaymath} Q^2 (\sigma,x_0) = 1 + q_x^2 \sigma^2 \left( \frac{1}{w_0 - ... ...x x_0} - \frac{4}{w_0 - 2 q_x x_0 + q_x^2 \sigma^2} \right)\;, \end{displaymath}$

(65)

where we must resolve 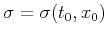$\sigma = \sigma (t_0,x_0)$ . This is done by revisiting equation D-8. For given

and

, $\sigma$ is the root of a depressed cubic function of the following form:

$\begin{displaymath} \sigma^3 + \frac{3 (w_0 - 2 q_x x_0)}{q_x^2} \sigma - \frac{3}{q_x^2} t_0 = 0\;. \end{displaymath}$

(66)

After some algebraic manipulations, we find

$\displaystyle \sigma (t_0,x_0)$	$\textstyle =$	$\displaystyle \left[ \frac{3 t_0 + \sqrt{9 t_0^2 + 4 (w_0 - 2 q_x x_0)^3 / q_x^2}}{2 q_x^2} \right]^{\frac{1}{3}}$
	$\textstyle -$	$\displaystyle \frac{w_0 - 2 q_x x_0}{q_x} \left[ \frac{2}{3 q_x t_0 + \sqrt{9 q_x^2 t_0^2 + 4 (w_0 - 2 q_x x_0)^3}} \right]^{\frac{1}{3}}\;.$	(67)

Finally, inserting equations D-10 and D-11 into equation 3 results in the Dix velocity:

$\begin{displaymath} v_d (t_0,x_0) = \frac{\sqrt{w_0 - 2 q_x x_0}}{w_0 - 2 q_x x_0 - q_x^2 \sigma^2}\;. \end{displaymath}$

(68)

Next: Bibliography Up: Li & Fomel: Time-to-depth Previous: Appendix C: Analytical expressions

2015-03-25