Next: Appendix D: Analytical expressions Up: Li & Fomel: Time-to-depth Previous: Appendix B: The Fréchet

Appendix C: Analytical expressions for the constant velocity gradient medium

In order to derive the time-to-depth conversion analytically, we first trace image rays in the depth coordinate for

and

. Then we carry out a direct inversion to find

and

. The Dix velocity can be obtained at last following equations 3 and 4.

Continuing from equation 15, we write the velocity in a coordinate relative to the image ray

$\begin{displaymath} v (z,x) = v_0 + g_z z + g_x x = \tilde{v}_0 + \mathbf{g} \cdot (\mathbf{x} - \mathbf{x_0})\;, \end{displaymath}$

(39)

where $\mathbf{g} = [g_z,g_x]^T$ and $\tilde{v}_0 = v_0 + g_x x_0$ . At the starting point, image ray satisfies

$\begin{displaymath} \left\{ \begin{array}{lcl} \mathbf{x_0} & = & [0, x_0]^T\;, ... ...ilde{v}_0^{-1}, 0]^T\;, \\ t_0 & = & t\;. \end{array} \right. \end{displaymath}$

(40)

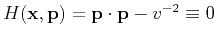Here we denote ray parameter $\mathbf{p} = \nabla t$ and $\mathbf{p_0}$ is the ray parameter at source. The Hamiltonian for ray tracing reads $H (\mathbf{x},\mathbf{p}) = \mathbf{p} \cdot \mathbf{p} - v^{-2} \equiv 0$ . The corresponding ray tracing system is (Cervený, 2001):

$\begin{displaymath} \left\{ \begin{array}{lcl} d \mathbf{x} / d \xi & = & \mathb... ...i = \mathbf{p} \cdot \mathbf{p} v^3 = v\;. \end{array} \right. \end{displaymath}$

(41)

Equation C-1 indicates $\nabla v = \mathbf{g}$ , which means $d \mathbf{p} / d \xi$ can be integrated analytically and provides

$\begin{displaymath} \mathbf{p} = \mathbf{p_0} - \mathbf{g} \xi\;. \end{displaymath}$

(42)

From the eikonal equation and considering 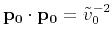$\mathbf{p_0} \cdot \mathbf{p_0} = \tilde{v}_0^{-2}$ and $g = \vert\mathbf{g}\vert = \sqrt{g_z^2 + g_x^2}$ , we have

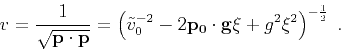$\begin{displaymath} v = \frac{1}{\sqrt{\mathbf{p} \cdot \mathbf{p}}} = \left( \... ..._0} \cdot \mathbf{g} \xi + g^2 \xi^2 \right)^{-\frac{1}{2}}\;. \end{displaymath}$

(43)

Integrating equation C-5 over 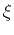$\xi$ gives

$\begin{displaymath} t = \frac{1}{g} \mathrm{arccosh} \left( 1 + \frac{g^2 \xi^2... ...lde{v}_0^{-1} - \mathbf{p_0} \cdot \mathbf{g} \xi} \right)\;. \end{displaymath}$

(44)

Meanwhile, combining equations C-1 and C-3, we find 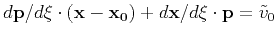$d \mathbf{p} / d \xi \cdot (\mathbf{x} - \mathbf{x_0}) + d \mathbf{x} / d \xi \cdot \mathbf{p} = \tilde{v}_0$ , i.e., $\mathbf{p} \cdot (\mathbf{x} - \mathbf{x_0}) = \tilde{v}_0 \xi$ . Suppose

$\begin{displaymath} \mathbf{x} - \mathbf{x_0} = \alpha \mathbf{p_0} + \beta \mathbf{g} \end{displaymath}$

(45)

then

$\begin{displaymath} \left\{ \begin{array}{lcl} \mathbf{g} \cdot (\mathbf{x} - \m... ...}_0 \xi + (v - \tilde{v}_0) \xi = v \xi\;. \end{array} \right. \end{displaymath}$

(46)

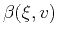Solving equation C-8 provides $\alpha (\xi,v)$ and $\beta (\xi,v)$ , which after substituting into equation C-7 leads to

$\begin{displaymath} \mathbf{x} = \mathbf{x_0} + \frac{(v - \tilde{v}_0) \left[\m... ...xi} {g^2 - (\mathbf{p_0} \cdot \mathbf{g})^2 \tilde{v}_0^2}\;. \end{displaymath}$

(47)

Note equation C-2 states $\mathbf{p_0} \cdot \mathbf{g} = g_z \tilde{v}_0^{-1}$ and thus equations C-4, C-6 and C-9 can be further simplified.

To connect depth- and time-domain attributes, we first invert equation C-6 such that 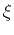$\xi$ is expressed by and

$\begin{displaymath} \xi (t_0,x_0) = \frac{g_z (1 - \cosh (\vert g t_0\vert)) + g \sinh (g t_0)}{g^2 \tilde{v}_0^2}\;. \end{displaymath}$

(48)

Next, we insert equations C-5 and C-10 into C-9 in order to change its parameterization from 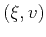$(\xi,v)$ to

. The result is written for the

and

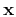components of $\mathbf{x}$ separately, as follows:

$\begin{displaymath} x (t_0,x_0) = x_0 + \frac{\tilde{v}_0 g_x (1 - \cosh (g t_0))}{g (g \cosh (g t_0) - g_z \sinh (g t_0))}\;, \end{displaymath}$

(49)

$\begin{displaymath} z (t_0,x_0) = \frac{\tilde{v}_0 \left[ g_z (1 - \cosh (g t_0... ... (g t_0) \right]} {g (g \cosh (g t_0) - g_z \sinh (g t_0))}\;. \end{displaymath}$

(50)

Inverting equations C-11 and C-12 results in

$\begin{displaymath} x_0 (z,x) = x + \frac{\sqrt{(v_0+g_x x)^2 + g_x^2 z^2} - (v_0 + g_x x)}{g_x}\;, \end{displaymath}$

(51)

$\begin{displaymath} t_0 (z,x) = \frac{1}{g} \mathrm{arccosh} \left\{ \frac{g^2 \... ...2 + g_x^2 z^2} + g_z z \right] - v g_z^2}{v g_x^2} \right\}\;. \end{displaymath}$

(52)

In the last step, we derive the analytical formula for the Dix velocity. Note that from equation C-13 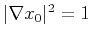$\vert\nabla x_0\vert^2 = 1$ , i.e., there is no geometrical spreading. The image rays are circles parallel to each other. Therefore according to equation 3 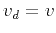and is found by combining equations C-5 and C-10

$\begin{displaymath} v_d (t_0,x_0) = \frac{(v_0 + g_x x_0) g}{g \cosh (g t_0) - g_z \sinh (g t_0)}\;. \end{displaymath}$

(53)

The time-migration velocity

, on the other hand, is

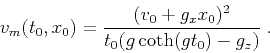$\begin{displaymath} v_m (t_0,x_0) = \frac{(v_0 + g_x x_0)^2}{t_0 ( g \coth (g t_0) - g_z )}\;. \end{displaymath}$

(54)

Next: Appendix D: Analytical expressions Up: Li & Fomel: Time-to-depth Previous: Appendix B: The Fréchet

2015-03-25