Next: Higher-order accuracy Up: Alkhalifah and Fomel: Source Previous: Shift in the source

A linear velocity model example

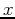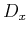As a first test to our formulations, we consider a 2-D model where the velocity changes linearly in the direction of the source perturbation. In this case, the traveltime is described analytically as a function of and and so will the traveltime changes, . Restricting this example to models with change of velocity in the direction of the source perturbation does not limit its generality since changes in the orthogonal direction has no direct influence on the traveltime field.

In the first example, we consider a source perturbation in the vertical direction in a medium in which the velocity changes linearly in the vertical direction. Considering source perturbation in the vertical direction is useful for applications related to datuming and possibly downward continuation. The linear velocity model is defined by

$\begin{displaymath} v(z) = v_0 + a z. \end{displaymath}$

(14)

where

is the vertical velocity gradient and

is velocity at the surface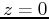

. The traveltime from a source at

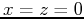to a point in the subsurface given by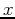

and

is provided by Slotnick (1959), as follows:

$\begin{displaymath} \tau(x,z) = \frac{1}{a} \cosh^{-1}\left(\frac{a^2 z^2 \left(\frac{x^2}{z^2}+1\right)}{2 v_0 \left(a z+v_0\right)}+1\right). \end{displaymath}$

(15)

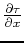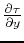Evaluating $\frac{\partial \tau}{\partial x}$ and $\frac{\partial \tau}{\partial y}$ and using equation 4 yields:

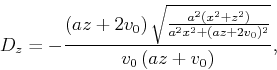$\begin{displaymath} D_z =- \frac{\left(a z+2 v_0\right) \sqrt{\frac{a^2 \left(x^... ... x^2+\left(a z+2 v_0\right){}^2}}}{v_0 \left(a z+v_0\right)}, \end{displaymath}$

(16)

which is an analytical representation of the change in the traveltime field shape with source depth location for this specific linear model and can be used to predict the traveltime for a source at a different depth. To test equation 16, we use equation 15 to estimate the traveltime using expansion 5 and compare that with the true traveltime for that source. 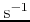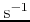Figure 2 shows this difference for a model with (a) a vertical velocity gradient of 0.5 $\mbox{s}^{-1}$ and (b) a vertical velocity gradient of 0.7 $\mbox{s}^{-1}$ . A 200 meter vertical shift, used here for the source, is typical of corrections applied in datuming among other applications. The errors, as expected, increase with an increase in velocity gradient as zero velocity gradient results in no change in traveltime shape and thus no errors. However, the errors are generally small for both gradients with the maximum value of 0.007 s occurring for the largest offset to depth ratio.

$diff2$
diff2 Figure 2. A color contour plot of the traveltime errors using the perturbation equation as a function of location () for a linear velocity model of with =2000 m/s and a vertical velocity gradient of 0.5 $s^{-1}$ for (a) and 0.7 $s^{-1}$ for (b). In both cases, the vertical source perturbation distance is 200 meters. The maximum traveltime errors are (a) 0.004 s and (b) 0.007 s.

In the second example, we consider source perturbation laterally in a medium in which the velocity changes linearly in the lateral direction. Considering source perturbation in the lateral direction could be useful for velocity estimation, beam based imaging, and interpolation applications, and more inline with the objectives of this study. In this case, the linear velocity model is defined by

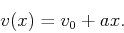$\begin{displaymath} v(x) = v_0 + a x. \end{displaymath}$

(17)

where

is now the lateral velocity gradient and

is velocity at the vertical line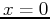

. The traveltime and

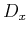are given by formulations similar to equations 15 and 16, but with an orthogonal transformation of coordinates. Though the equations are similar, we want to get an estimate of the error distribution for this problem. Figure 3 shows the traveltime errors for using these new formula to predict the changes due to shifts in the source location by (a) 100 meters and (b) 200 meters. As expected, the errors increase with the amount of shift. However, in both cases the errors are generally small and bounded by 0.002 s.

$diffx2$
diffx2 Figure 3. A color contour plot of the traveltime errors using the perturbation equation as a function of location () for a linear velocity model of with =2000 m/s and a horizontal velocity gradient of 0.5 $s^{-1}$ for (a) a horizontal source perturbation of 100 meters and (b) a horizontal source perturbation distance of 200 meters. The maximum traveltime errors are (a) 0.0005 s and (b) 0.002 s.

$diffx2$

diffx2
Figure 3. A color contour plot of the traveltime errors using the perturbation equation as a function of location (

) for a linear velocity model of with

=2000 m/s and a horizontal velocity gradient of 0.5 $s^{-1}$ for (a) a horizontal source perturbation of 100 meters and (b) a horizontal source perturbation distance of 200 meters. The maximum traveltime errors are (a) 0.0005 s and (b) 0.002 s.

Next: Higher-order accuracy Up: Alkhalifah and Fomel: Source Previous: Shift in the source

2013-04-02