 |
 |
 |
 | An eikonal based formulation for traveltime
perturbation with respect to the source location |  |
![[pdf]](icons/pdf.png) |
Next: A linear velocity model
Up: Alkhalifah and Fomel: Source
Previous: Introduction
The eikonal equation appears in the zeroth-order asymptotic expansion
of the solution of the wave equation given by the Wentzel, Kramers,
and Brillouin (WKB) approximation. It represents
the geometrical optics term that contains the most rapidly varying
component of the leading behavior of the expansion. In a medium with
sloth (slowness squared), 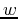 , the traveltime
, the traveltime 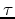 for a wavefield
emanating from a source satisfies the following formula:
for a wavefield
emanating from a source satisfies the following formula:
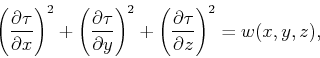 |
(1) |
where  are the components of the 3-D medium. At the location
of the source
are the components of the 3-D medium. At the location
of the source  , the initial value of time
, the initial value of time
 is needed for numerically solving the eikonal
equation 1. Moving the source along the
is needed for numerically solving the eikonal
equation 1. Moving the source along the 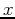 -axis a
distance
-axis a
distance 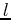 is equivalent to solving the following eikonal equation:
is equivalent to solving the following eikonal equation:
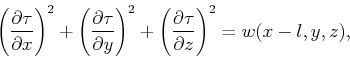 |
(2) |
for the same source location. In other words, we are replacing a shift in the source location with an equal distance shift in the velocity field
in the opposite direction.
Figure 1 shows the operation for a single source and image point combination
taking into account the reciprocity principle between sources and receivers.
timeds
Figure 1. Illustration of the relation between the
initial source location and a perturbed version given by a single
source and image point locations. This is equivalent to a shift in
the velocity field laterally by 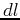 . .
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
Assuming that the sloth (or velocity) field is continuous in the 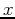 direction, we differentiate equation 2 with respect
to
direction, we differentiate equation 2 with respect
to 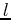 and get:
and get:
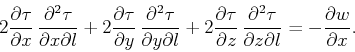 |
(3) |
Substituting the change in traveltime field shape due to source
perturbation,
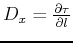 , into
equation 3 provides a first order linear equation in
, into
equation 3 provides a first order linear equation in
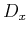 given by:
given by:
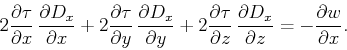 |
(4) |
Solving for  requires the velocity (sloth) field as well as the traveltime field
requires the velocity (sloth) field as well as the traveltime field  for a source located at the surface at
for a source located at the surface at  . Thus,the
traveltime field for a source at
. Thus,the
traveltime field for a source at 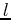 can be approximated by
can be approximated by
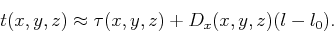 |
(5) |
Equation 4 is velocity dependent, which limits its use for inversion purposes.
However, a differentiation of Equation 2 with respect to 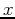 produces
produces
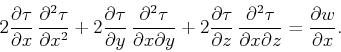 |
(6) |
Adding equations 3 and 6 yields equation
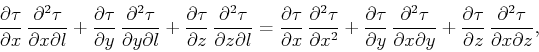 |
(7) |
which is velocity independent. Substituting again the change in
traveltime with source location
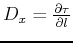 into equation 7 yields
into equation 7 yields
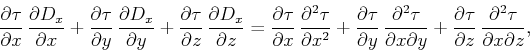 |
(8) |
which is a first order linear partial differential equation in 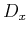 with
with 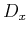 =0 at the source. The traveltime derivatives are computed
for a given traveltime field
=0 at the source. The traveltime derivatives are computed
for a given traveltime field 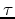 corresponding to a source location
corresponding to a source location
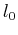 . Equation 8 can be represented in a vector
notation as follows:
. Equation 8 can be represented in a vector
notation as follows:
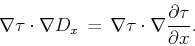 |
(9) |
A similar treatment for a change of the source location in 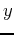 or
or  yields the following equations, respectively:
yields the following equations, respectively:
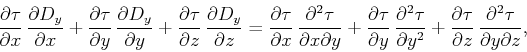 |
(10) |
or
 |
(11) |
and
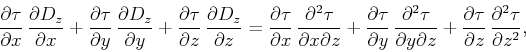 |
(12) |
or
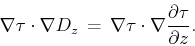 |
(13) |
The above set of equations provides a tool for calculating first-order
traveltime derivatives with respect to the source location. However,
a condition for stability is that the velocity field must be
continuous. This condition is analogous to conditions used in ray
tracing methods and can be enforced using smoothing
techniques. Another approach to handle this limitation is discussed
later.
 |
 |
 |
 | An eikonal based formulation for traveltime
perturbation with respect to the source location |  |
![[pdf]](icons/pdf.png) |
Next: A linear velocity model
Up: Alkhalifah and Fomel: Source
Previous: Introduction
2013-04-02
![]() , the traveltime
, the traveltime ![]() for a wavefield
emanating from a source satisfies the following formula:
for a wavefield
emanating from a source satisfies the following formula:

![]() direction, we differentiate equation 2 with respect
to
direction, we differentiate equation 2 with respect
to ![]() and get:
and get:
![]() produces
produces
![]() or
or ![]() yields the following equations, respectively:
yields the following equations, respectively: