 |
 |
 |
 | Velocity continuation and the anatomy of
residual prestack time migration |  |
![[pdf]](icons/pdf.png) |
Next: Dynamics of Residual DMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: Dynamics of Zero-Offset Velocity
According to the theory of characteristics, described in the beginning
of this section, the kinematic residual NMO equation
(22) corresponds to the dynamic equation of the form
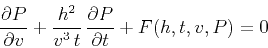 |
(44) |
with the undetermined function 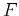 . In the case of
. In the case of 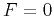 , the
general solution
is easily found to be
, the
general solution
is easily found to be
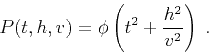 |
(45) |
where 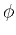 is an arbitrary smooth function.
The combination of dynamic equations (44) and
(41) leads to an approximate prestack velocity
continuation with the residual DMO effect neglected. To accomplish the
combination, one can simply add the term
is an arbitrary smooth function.
The combination of dynamic equations (44) and
(41) leads to an approximate prestack velocity
continuation with the residual DMO effect neglected. To accomplish the
combination, one can simply add the term
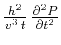 from
equation (44) to the left-hand
side of equation (41). This addition changes the
kinematics of velocity continuation, but does not change the amplitude
properties embedded in the transport equation (42).
from
equation (44) to the left-hand
side of equation (41). This addition changes the
kinematics of velocity continuation, but does not change the amplitude
properties embedded in the transport equation (42).
Dunkin and Levin (1973) and Hale (1983) advocate using
an amplitude correction term in the NMO step. This term can be
easily added by selecting an appropriate function 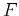 in
equation (44). The choice
in
equation (44). The choice
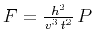 results in the equation
results in the equation
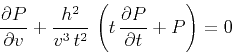 |
(46) |
with the general solution
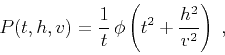 |
(47) |
which has the Dunkin-Levin amplitude correction term.
 |
 |
 |
 | Velocity continuation and the anatomy of
residual prestack time migration |  |
![[pdf]](icons/pdf.png) |
Next: Dynamics of Residual DMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: Dynamics of Zero-Offset Velocity
2014-04-01
![]() in
equation (44). The choice
in
equation (44). The choice
![]() results in the equation
results in the equation