 |
 |
 |
 | Velocity continuation and the anatomy of
residual prestack time migration |  |
![[pdf]](icons/pdf.png) |
Next: Dynamics of Residual NMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: FROM KINEMATICS TO DYNAMICS
In the case of zero-offset velocity continuation, the characteristic
equation is reconstructed from equation (2) to have
the form
 |
(36) |
where 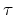 is replaced by
is replaced by  according to
equation (35). According to
equation (32), the corresponding dynamic equation is
according to
equation (35). According to
equation (32), the corresponding dynamic equation is
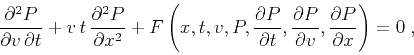 |
(37) |
where the function 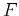 remains to be defined. The simplest case of
remains to be defined. The simplest case of 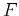 equal to zero corresponds to Claerbout's velocity continuation
equation (Claerbout, 1986), derived in a different way.
Levin (1986a) provides the dispersion-relation derivation,
conceptually analogous to applying the method of characteristics.
equal to zero corresponds to Claerbout's velocity continuation
equation (Claerbout, 1986), derived in a different way.
Levin (1986a) provides the dispersion-relation derivation,
conceptually analogous to applying the method of characteristics.
In high-frequency asymptotics, the wavefield  can be
represented by the ray-theoretical (WKBJ) approximation,
can be
represented by the ray-theoretical (WKBJ) approximation,
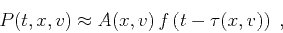 |
(38) |
where  is the amplitude,
is the amplitude, 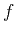 is the short (high-frequency) wavelet,
and the function
is the short (high-frequency) wavelet,
and the function 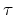 satisfies the kinematic equation
(2). Substituting approximation (38) into
the dynamic velocity continuation equation (37),
collecting the leading-order terms, and neglecting the
satisfies the kinematic equation
(2). Substituting approximation (38) into
the dynamic velocity continuation equation (37),
collecting the leading-order terms, and neglecting the 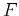 function
leads to the partial differential equation for amplitude transport:
function
leads to the partial differential equation for amplitude transport:
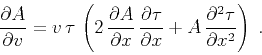 |
(39) |
The general solution of equation (39) follows from the
theory of characteristics. It takes the form
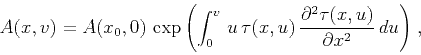 |
(40) |
where the integral corresponds to the
curvilinear integration along the corresponding velocity ray, and  corresponds to the
starting point of the ray.
In the case of a plane dipping reflector, the image of the reflector remains
plane in the velocity continuation process. Therefore, the second
traveltime derivative
corresponds to the
starting point of the ray.
In the case of a plane dipping reflector, the image of the reflector remains
plane in the velocity continuation process. Therefore, the second
traveltime derivative
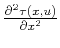 in
(40) equals zero, and the exponential is equal to
one. This means that the amplitude of the image does not change with
the velocity along the velocity rays. This fact does not agree with the
theory of conventional post-stack migration, which suggests
downscaling the image by the ``cosine'' factor
in
(40) equals zero, and the exponential is equal to
one. This means that the amplitude of the image does not change with
the velocity along the velocity rays. This fact does not agree with the
theory of conventional post-stack migration, which suggests
downscaling the image by the ``cosine'' factor
 (Levin, 1986b; Chun and Jacewitz, 1981). The simplest way to
include the cosine factor in the velocity continuation equation is to
set the function
(Levin, 1986b; Chun and Jacewitz, 1981). The simplest way to
include the cosine factor in the velocity continuation equation is to
set the function 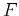 to be
to be
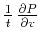 . The resulting differential equation
. The resulting differential equation
 |
(41) |
has the amplitude transport
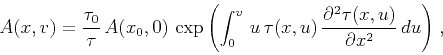 |
(42) |
corresponding to the differential equation
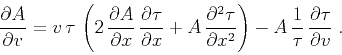 |
(43) |
Appendix C proves that the time-and-space solution of the dynamic
velocity continuation equation (41) coincides with the
conventional Kirchhoff migration operator.
 |
 |
 |
 | Velocity continuation and the anatomy of
residual prestack time migration |  |
![[pdf]](icons/pdf.png) |
Next: Dynamics of Residual NMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: FROM KINEMATICS TO DYNAMICS
2014-04-01
![]() can be
represented by the ray-theoretical (WKBJ) approximation,
can be
represented by the ray-theoretical (WKBJ) approximation,