Generalized nonhyperbolic moveout approximation

Appendix D: REFLECTION FROM A CIRCULAR REFLECTOR IN A HOMOGENEOUS VELOCITY MODEL

In the case of a circular (cylindrical or spherical) reflector in a homogeneous velocity model, there is no closed-form analytical solution. However, the moveout can be described analytically by parametric relationships (Glaeser, 1999).

crefl
Figure 10. Reflection from a circular reflector in a homogeneous velocity model (a scheme).

Consider the geometry of the reflection shown in Figure D-1. According to the trigonometry of the reflection triangles, the source and receiver positions can be expressed as

$$x_s = R\,\sin{\alpha} + (H+R - R\,\cos{\alpha})\,\tan{(\alpha-\theta)}\;,$$ (67)

$$x_r = R\,\sin{\alpha} + (H+R - R\,\cos{\alpha})\,\tan{(\alpha+\theta)}\;,$$ (68)

where $R$ is the reflector radius, $H$ is the minimum reflector depth, $\alpha$ is the reflector dip angle at the reflection point, and $\theta$ is the reflection angle. Correspondingly, the midpoint and offset coordinates can be expressed as

$$m = \frac{x_s+x_r}{2} = R\,\sin{\alpha} + (H+R - R\,\cos{\alpha})\,\frac{\cos{\alpha}\,\sin{\alpha}}{\cos^2{\theta} - \sin^2{\alpha}}\;,$$ (69)

$$x = x_r - x_s = 2\,(H+R - R\,\cos{\alpha})\,\frac{\cos{\theta}\,\sin{\theta}}{\cos^2{\theta} - \sin^2{\alpha}}\;,$$ (70)

and the reflection traveltime can be expressed as

$$t = \frac{H+R - R\,\cos{\alpha}}{V}\,\left[\frac{1}{\cos{(\alpha-\theta)}} + \frac{1}{\cos{(\alpha+\theta)}}\right]$$

$$= 2\,\frac{H+R - R\,\cos{\alpha}}{V}\,\frac{\cos{\alpha}\,\cos{\theta}}{\cos^2{\theta} - \sin^2{\alpha}}\;,$$ (71)

where $V$ is the medium velocity. Expressing the reflection angle $\theta$ from equation D-3 and substituting it into equations D-4 and D-5, we obtain a pair of parametric equations

$$x^2(\alpha) = 4\,\frac{[m\,\cos{\alpha} - (H+R)\,\sin{\alpha}]\,[m\,\sin{\alpha} + (H+R)\,\cos{\alpha} - R]}{\cos{\alpha}\,\sin{\alpha}}\;,$$ (72)

$$t^2(\alpha) = \frac{4}{V^2}\,\frac{(m - R\,\sin{\alpha})\,[m\,\sin{\alpha} + (H+R)\,\cos{\alpha} - R]}{\sin{\alpha}}\;,$$ (73)

which define the exact reflection moveout for the case of a circular reflector in a homogeneous medium.

The connection with parameters of equations 27-29 is given by

$$L = \sqrt{m^2 + (H+R)^2} - R\;,$$ (74)

$$\cos{\beta} = \frac{H+R}{\sqrt{m^2 + (H+R)^2}}\;,$$ (75)

$$G = \frac{L}{L+R} = 1 - \frac{R}{\sqrt{m^2 + (H+R)^2}}\;.$$ (76)

The behavior of the moveout at infinitely large offsets is controlled by $P_{\infty} = 1/V$ and

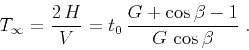$$T_{\infty} = \frac{2\,H}{V} = t_0\,\frac{G+\cos{\beta} - 1}{G\,\cos{\beta}}\;.$$ (77)

After substitution in equations 25-26, we obtain somewhat complicated but analytical expressions for parameters $B$ and $C$.

Generalized nonhyperbolic moveout approximation