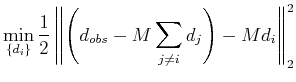|
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Seislet-based MCA sparsified with
Up: MCA with scale-dependent shaping
Previous: Understanding iterative thresholding as
MCA considers the complete data 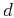 to be the superposition of several morphologically distinct components:
to be the superposition of several morphologically distinct components:
 . For each component
. For each component 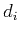 , MCA assumes there exists a transform
, MCA assumes there exists a transform 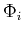 which can sparsely represent component
which can sparsely represent component 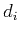 by its coefficients
by its coefficients 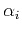 (
(
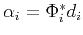 should be sparse), and can not do so for the others. Mathematically,
should be sparse), and can not do so for the others. Mathematically,
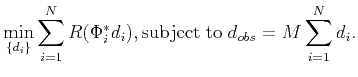 |
(11) |
The above problem can be rewritten as
 |
(12) |
We prefer to rewrite Eq. (12) as
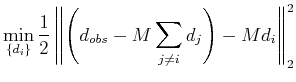 |
|
|
|
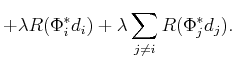 |
|
|
(13) |
Thus, optimizing with respect to 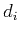 leads to the analysis IST shaping as Eq. (9). At the kth iteration, optimization is performed alternatively for many components using the block coordinate relaxation (BCR) technique (Bruce et al., 1998): for the ith component
leads to the analysis IST shaping as Eq. (9). At the kth iteration, optimization is performed alternatively for many components using the block coordinate relaxation (BCR) technique (Bruce et al., 1998): for the ith component 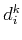 ,
,
 :
:
 ,
,
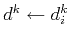 ,
,
 ,
,
 , yields the residual term
, yields the residual term
 and the updating rule
and the updating rule
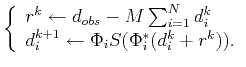 |
(14) |
The final output of the above algorithm are the morphological components
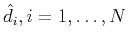 . The complete data can then be reconstructed via
. The complete data can then be reconstructed via
 .
This is the main principle of the so-called MCA-based inpainting algorithm (Elad et al., 2005).
.
This is the main principle of the so-called MCA-based inpainting algorithm (Elad et al., 2005).
 |
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Seislet-based MCA sparsified with
Up: MCA with scale-dependent shaping
Previous: Understanding iterative thresholding as
2021-08-31
![]() to be the superposition of several morphologically distinct components:
to be the superposition of several morphologically distinct components:
![]() . For each component
. For each component ![]() , MCA assumes there exists a transform
, MCA assumes there exists a transform ![]() which can sparsely represent component
which can sparsely represent component ![]() by its coefficients
by its coefficients ![]() (
(
![]() should be sparse), and can not do so for the others. Mathematically,
should be sparse), and can not do so for the others. Mathematically,