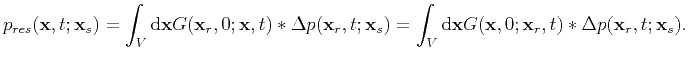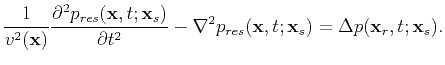|
 |
 |
 | A graphics processing unit implementation of time-domain full-waveform inversion |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Yang et al.: GPU
Previous: Discussion
The work of the first author is supported by China Scholarship Council during his visit to Bureau of Economic Geology, The University of Texas at Austin.
This work is sponsored by National Science Foundation of China (No. 41390454). Thanks go to IFP for the Marmousi model. We wish to thank Sergey Fomel for valuable help to incorporate the codes into Madagascar software package (Fomel et al., 2013) (http://www.ahay.org), which makes all the numerical examples reproducible. The paper is substantially improved according to the suggestions of Joe Dellinger, Robin Weiss and two other reviewers.
Appendix
A
Misfit function minimization
Here, we mainly follow the delineations of FWI by Pratt et al. (1998) and Virieux and Operto (2009).The minimum of the misfit function
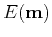 is sought in the vicinity of the starting model
is sought in the vicinity of the starting model
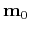 . The FWI is essentially a local optimization.
In the framework of the Born approximation, we assume that the updated model
. The FWI is essentially a local optimization.
In the framework of the Born approximation, we assume that the updated model
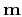 of dimension
of dimension  can be written as the sum of the starting model
can be written as the sum of the starting model
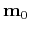 plus a perturbation model
plus a perturbation model
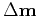 :
:
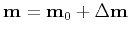 . In the following, we assume that
. In the following, we assume that
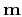 is real valued.
is real valued.
A second-order Taylor-Lagrange development of the misfit function in the vicinity of
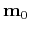 gives the expression
gives the expression
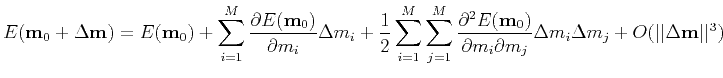 |
(17) |
Taking the derivative with respect to the model parameter 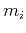 results in
results in
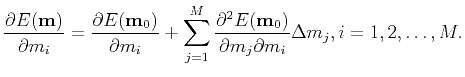 |
(18) |
Equation (A-2) can be abbreviated as
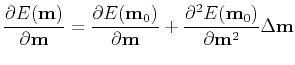 |
(19) |
Thus,
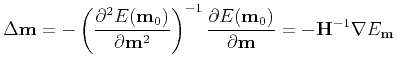 |
(20) |
where
![$\displaystyle \nabla E_{\textbf{m}}=\frac{\partial E(\textbf{m}_0)}{\partial \t...
...}{\partial m_2}, \ldots, \frac{\partial E(\textbf{m}_0)}{\partial m_M}\right]^T$](img75.png) |
(21) |
and
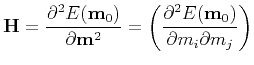 |
(22) |
 and
and
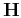 are the gradient vector and the Hessian matrix, respectively.
are the gradient vector and the Hessian matrix, respectively.
![$\displaystyle \nabla E_{\textbf{m}}=\nabla E(\textbf{m})=\frac{\partial E(\text...
...textbf{p}\right] =\mathtt{Re}\left[\textbf{J}^{\dagger}\Delta \textbf{p}\right]$](img79.png) |
(23) |
where
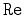 takes the real part, and
takes the real part, and
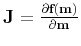 is the Jacobian matrix, i.e., the sensitivity or the Fréchet derivative matrix.
is the Jacobian matrix, i.e., the sensitivity or the Fréchet derivative matrix.
In matrix form
![$\displaystyle \textbf{H}=\frac{\partial^2 E(\textbf{m})}{\partial \textbf{m}^2}...
...(\Delta \textbf{p}^*, \Delta \textbf{p}^*, \ldots, \Delta \textbf{p}^*)\right].$](img82.png) |
(24) |
In the Gauss-Newton method, this second-order term is neglected for nonlinear inverse problems. In the following, the remaining term in the Hessian, i.e.,
![$ \textbf{H}_a=\mathtt{Re}[\textbf{J}^{\dagger}\textbf{J}]$](img83.png) , is referred to as the approximate Hessian. It is the auto-correlation of the derivative wavefield. Equation (A-4) becomes
, is referred to as the approximate Hessian. It is the auto-correlation of the derivative wavefield. Equation (A-4) becomes
![$\displaystyle \Delta \textbf{m} =-\textbf{H}^{-1}\nabla E_{\textbf{m}} =-\textbf{H}_a^{-1}\mathtt{Re}[\textbf{J}^{\dagger}\Delta \textbf{p}].$](img84.png) |
(25) |
To guarantee the stability of the algorithm (avoiding the singularity), we may use
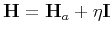 , leading to
, leading to
![$\displaystyle \Delta \textbf{m} =-\textbf{H}^{-1}\nabla E_{\textbf{m}} =-(\text...
... \textbf{I})^{-1}\mathtt{Re}\left[\textbf{J}^{\dagger}\Delta \textbf{p}\right].$](img86.png) |
(26) |
Alternatively, the inverse of the Hessian in equation (A-4) can be replaced by
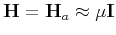 , leading to the gradient or steepest-descent method:
, leading to the gradient or steepest-descent method:
![$\displaystyle \Delta \textbf{m} =-\mu^{-1}\nabla E_{\textbf{m}} =-\alpha\nabla ...
...xtbf{m}} =-\alpha\mathtt{Re}\left[\textbf{J}^{\dagger}\Delta \textbf{p}\right].$](img88.png) |
(27) |
where
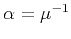 .
.
Appendix
B
Fréchet derivative
Recall that the basic acoustic wave equation reads
The Green's function
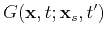 is defined by
is defined by
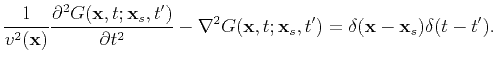 |
(28) |
Thus the integral representation of the solution can be given by (Tarantola, 1984)
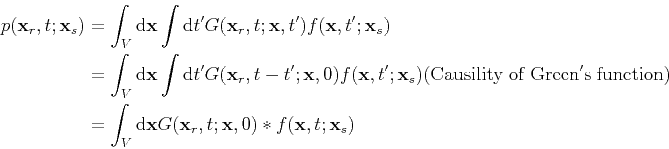 |
(29) |
where  denotes the convolution operator.
denotes the convolution operator.
A perturbation
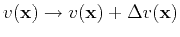 will produce a field
will produce a field
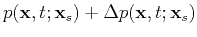 defined by
defined by
![$\displaystyle \frac{1}{(v(\textbf{x})+\Delta v(\textbf{x}))^2}\frac{\partial^2 ...
...xtbf{x}_s)+\Delta p(\textbf{x},t;\textbf{x}_s)] =f_s(\textbf{x},t;\textbf{x}_s)$](img96.png) |
(30) |
Note that
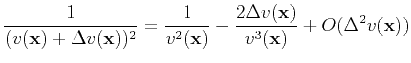 |
(31) |
Equation (B-3) subtracts equation (1), yielding
![$\displaystyle \frac{1}{v^2(\textbf{x})}\frac{\partial^2 \Delta p(\textbf{x},t;\...
...x},t;\textbf{x}_s)]}{\partial t^2}\frac{2\Delta v(\textbf{x})}{v^3(\textbf{x})}$](img98.png) |
(32) |
Using the Born approximation, equation (B-5) becomes
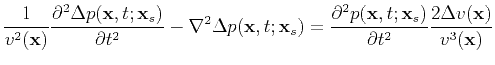 |
(33) |
Again, based on integral representation, we obtain
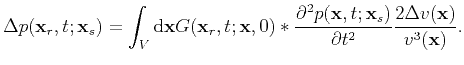 |
(34) |
Appendix
C
Gradient computation
In terms of equation (2),
![\begin{displaymath}\begin{split}\frac{\partial E(\textbf{m})}{\partial m_i} &=\f...
...^{\dagger}\Delta \textbf{p}\right], i=1,2,\ldots,M. \end{split}\end{displaymath}](img101.png) |
(35) |
According to the previous section, it follows that
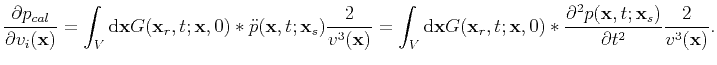 |
(36) |
The convolution guarantees
![$\displaystyle \int \mathrm{d}t [g(t)*f(t)]h(t)=\int \mathrm{d}t f(t)[g(-t)*h(t)].$](img103.png) |
(37) |
Then, equation (C-1) becomes
![\begin{displaymath}\begin{split}\frac{\partial E(\textbf{m})}{\partial m_i} &=\s...
...ght)^*p_{res}(\textbf{x}_r,t;\textbf{x}_s)\right]\\ \end{split}\end{displaymath}](img104.png) |
(38) |
where
 is a time-reversal wavefield produced using the residual
is a time-reversal wavefield produced using the residual
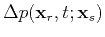 as the source. As follows from reciprocity theorem,
as the source. As follows from reciprocity theorem,
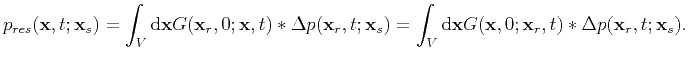 |
(39) |
satisfying
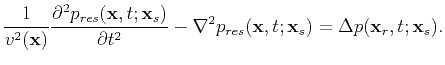 |
(40) |
It is noteworthy that an input 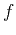 and the system impulse response function
and the system impulse response function 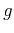 are exchangeable in convolution. That is to say, we can use the system impulse response function
are exchangeable in convolution. That is to say, we can use the system impulse response function 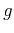 as the input, the input
as the input, the input 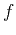 as the impulse response function, leading to the same output. In the seismic modeling and acquisition process, the same seismogram can be obtained when we shoot at the receiver position
as the impulse response function, leading to the same output. In the seismic modeling and acquisition process, the same seismogram can be obtained when we shoot at the receiver position
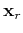 when recording the seismic data at position
when recording the seismic data at position
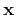 .
.
 |
 |
 |
 | A graphics processing unit implementation of time-domain full-waveform inversion |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Yang et al.: GPU
Previous: Discussion
2021-08-31
![]() is sought in the vicinity of the starting model
is sought in the vicinity of the starting model
![]() . The FWI is essentially a local optimization.
In the framework of the Born approximation, we assume that the updated model
. The FWI is essentially a local optimization.
In the framework of the Born approximation, we assume that the updated model
![]() of dimension
of dimension ![]() can be written as the sum of the starting model
can be written as the sum of the starting model
![]() plus a perturbation model
plus a perturbation model
![]() :
:
![]() . In the following, we assume that
. In the following, we assume that
![]() is real valued.
is real valued.
![]() gives the expression
gives the expression
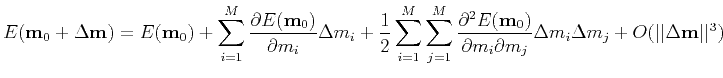
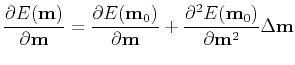
![$\displaystyle \nabla E_{\textbf{m}}=\frac{\partial E(\textbf{m}_0)}{\partial \t...
...}{\partial m_2}, \ldots, \frac{\partial E(\textbf{m}_0)}{\partial m_M}\right]^T$](img75.png)
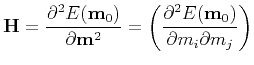
![]() , leading to
, leading to
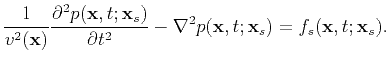
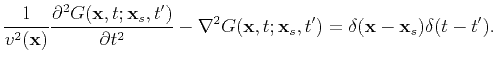
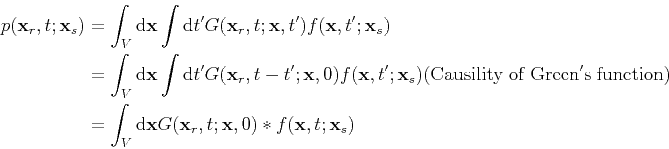
![]() will produce a field
will produce a field
![]() defined by
defined by
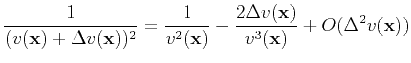
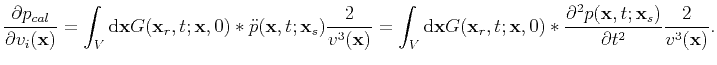
![$\displaystyle \int \mathrm{d}t [g(t)*f(t)]h(t)=\int \mathrm{d}t f(t)[g(-t)*h(t)].$](img103.png)
![\begin{displaymath}\begin{split}\frac{\partial E(\textbf{m})}{\partial m_i} &=\s...
...ght)^*p_{res}(\textbf{x}_r,t;\textbf{x}_s)\right]\\ \end{split}\end{displaymath}](img104.png)