 |
 |
 |
 | Time-to-depth conversion and seismic velocity estimation using time-migration velocity |  |
![[pdf]](icons/pdf.png) |
Next: Inversion Methods
Up: Partial differential equations for
Previous: 3-D case
Equations 14 and 20 reveal the nature of the
instabilities in the problem in hand. These PDEs are elliptic, while
the physical setting allows us to pose only a Cauchy problem for
them, which is well-known to be ill-posed. Furthermore, the fact that
the PDEs involve not only the Dix velocity itself, but also its first
and second derivatives, leads to high sensitivity of the solutions to
input data.
Nonetheless, we found two ways
for solving these PDEs numerically on the required,
and relatively short,
interval of time: namely,
a finite difference scheme inspired by the Lax-Friedrichs
method and a spectral Chebyshev method.
A detailed analysis of the problem shows that our methods work thanks to
- the special input
 , corresponding
to a positive finite seismic velocity;
, corresponding
to a positive finite seismic velocity;
- the special initial conditions
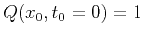 ,
,
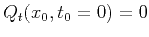 corresponding to the image rays;
corresponding to the image rays;
- the fact that
our finite difference method contains error
terms which damp the high harmonics;
truncation of the polynomial series in the
spectral Chebyshev method which is similar to truncation
of the high harmonics; and
- the short interval of time, in which we need to compute the solution,
so that the growing low harmonics fail to develop significantly.
Items 1 and 2 say that the exact solutions of our PDEs for the
hypothetical perfect Dix velocity given by equations 10
and 11 are finite and nonzero. Items 3 and 4 say that the
numerical methods take care of the imperfection of the data and
computations on a short enough time interval.
 |
 |
 |
 | Time-to-depth conversion and seismic velocity estimation using time-migration velocity |  |
![[pdf]](icons/pdf.png) |
Next: Inversion Methods
Up: Partial differential equations for
Previous: 3-D case
2013-07-26