Time-to-depth conversion and seismic velocity estimation using time-migration velocity

Seismic Velocity

In this section, we will establish theoretical relationships between time-migration velocity and seismic velocity in 2-D and 3-D.

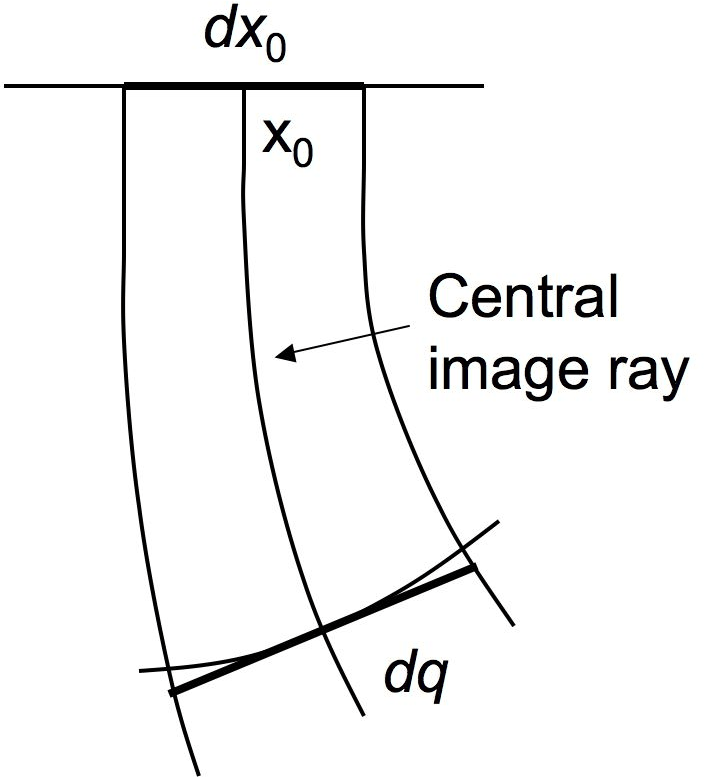
The seismic velocity and the Dix velocity are connected through the quantity $\mathbf{Q}$ , the geometrical spreading of image rays. $\mathbf{Q}$ is a scalar in 2-D and a $2\times 2$ matrix in 3-D. The simplest way to introduce $\mathbf{Q}$ is the following. Trace an image ray $\mathbf{x}(\mathbf{x}_0,t)$ . $\mathbf{x}_0$ is the starting surface point, $t$ is the traveltime. Call this ray central. Consider a small tube of rays around it. All these rays start from a small neighborhood $d\mathbf{x}_0$ of the point $\mathbf{x}_0$ perpendicular to the earth surface. Thus, they represent a fragment of a plane wave propagating downward. Consider the fragment of the wave front defined by this ray tube at time $t_0$ . Let $d\mathbf{q}$ be the fragment of the tangent to the front at the point $\mathbf{x}(\mathbf{x}_0,t_0)$ reached by the central ray at time $t_0$ , bounded by the ray tube (Figure 1). Then, in 2-D, $Q$ is the derivative $Q(x_0,t_0)=\frac{dq}{dx_0}$ . In 3-D, $\mathbf{Q}$ is the matrix of the derivatives $\mathbf{Q}_{ij}(\mathbf{x}_0,t_0)= \frac{d\mathbf{q}_i}{d\mathbf{x}_{0j}}$ , $i,j=1,2$ , where derivatives are taken along certain mutually orthogonal directions $\mathbf{e}_1$ , $\mathbf{e}_2$ (Popov, 2002; Popov and Pšencik, 1978; Cervený, 2001).

Qdef
Figure 1. Illustration for the definition of geometrical spreading.

The time evolution of the matrices $\tensor{Q}$ and $\tensor{P}$ is given by

$$\frac{d}{dt}\left(\begin{array}{c}\tensor{Q}\\ \tensor{P}\end{arr... ...{array}\right) \left(\begin{array}{c}\tensor{Q}\\ \tensor{P}\end{array}\right),$$ (9)

where $v_0$ it the velocity at the central ray at time $t$ , $\tensor{V}=\left(\frac{\partial^2 v}{\partial q_i\partial q_j}\right)_{i,j=1,2}$ , and $\tensor{I}$ is the $2\times 2$ identity matrix. The absolute value of $\det \mathbf{Q}$ has a simple meaning: it is the geometrical spreading of the image rays (Popov, 2002; Popov and Pšencik, 1978; Cervený, 2001). The matrix $\tensor{\Gamma}$ , introduced in the previous section, relates to $\tensor{Q}$ and $\tensor{P}$ as $\tensor{\Gamma}=\tensor{P}\tensor{Q}^{-1}$ . Hence, $\tensor{K}=\tensor{Q}\tensor{P}^{-1}$ .

In (Cameron et al., 2007), we have proven that

$$v_{Dix}(x_0,t_0)\equiv\sqrt{\frac{\partial}{\partial t_0} \left(t_0v_m^2(x_0,t_0)\right)}= \frac{v(x(x_0,t_0),z(x_0,t_0))}{\vert Q(x_0,t_0)\vert}$$ (10)

in 2-D, where $v_m(x_0,t_0)$ is the time-migration velocity, and

$$\frac{\partial}{\partial t_0} \left(\tensor{K}(\mathbf{x}_0,t_0)\... ...))\left(\mathbf{Q}(\mathbf{x}_0,t_0) \mathbf{Q}^T(\mathbf{x}_0,t_0)\right)^{-1}$$ (11)

in 3-D, $\tensor{K}$ is defined by equation 6 and can be determined from equation 7.

Time-to-depth conversion and seismic velocity estimation using time-migration velocity