|
|
|
|
Omnidirectional plane-wave destruction |
The combined linear system can be solved analytically. It
is based on the property that
![]() can be
decoupled into the product of two terms,
as shown in the appendix,
can be
decoupled into the product of two terms,
as shown in the appendix,
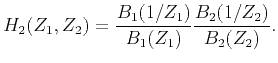 |
(15) |
![]() and
and ![]() can be designed
in the same way as for the line-interpolating PWD,
whose coefficients are given by
equation 5.
can be designed
in the same way as for the line-interpolating PWD,
whose coefficients are given by
equation 5.
![]() can be implemented by applying the 1D maxflat filter
on each direction independently.
can be implemented by applying the 1D maxflat filter
on each direction independently.
This separability of the maxflat linear phase filter extends to 3D and higher dimensions.
|
|
|
|
Omnidirectional plane-wave destruction |