|
|
|
|
Least-squares non-stationary triangle smoothing |
Next: Estimating the Smoothing Radius Up: Alomar and Fomel: Non-stationary Previous: Triangle Smoothing
 :
To obtain the time domain implementation of the triangle smoothing derivative, we break down equation 8 into three parts to obtain the following three step implementation:
:
To obtain the time domain implementation of the triangle smoothing derivative, we break down equation 8 into three parts to obtain the following three step implementation:
![$\left[\frac{-i \Delta t \sin(\frac{R\omega \Delta t}{2})}{2R^2\sin^2(\frac{\omega \Delta t}{2})}\right]$](img20.png) in equation 8
in equation 8
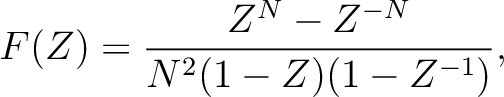 |
(9) |
 |
(10) |
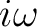 in equation 8.
in equation 8.
 . This step corresponds to the term
. This step corresponds to the term
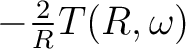 in equation 8.
in equation 8.
 |
(12) |