|
|
|
|
Least-squares non-stationary triangle smoothing |
Next: Triangle Smoothing Derivative Up: Alomar and Fomel: Non-stationary Previous: Introduction
 |
(1) |
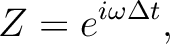 |
(2) |
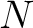 is the number of samples included in a moving average under a rectangle window,
is the number of samples included in a moving average under a rectangle window,  is the frequency in radians, and
is the frequency in radians, and 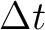 is the interval spacing in time. Division by
is the interval spacing in time. Division by  is the operation of causal integration and corresponds to the following recursion in time:
The adjoint of this operation is anti-causal integration, or division by
is the operation of causal integration and corresponds to the following recursion in time:
The adjoint of this operation is anti-causal integration, or division by
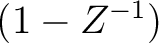 , and is represented by the backward recursion in time:
A triangle filter is defined as the cross-correlation of two box filters (Claerbout, 1992)
, and is represented by the backward recursion in time:
A triangle filter is defined as the cross-correlation of two box filters (Claerbout, 1992)
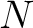 becomes the triangle smoothing radius, or half the number of points included in a moving average under a triangle window. The numerator in 5 is represented by the following filtering operation:
Triangle smoothing is efficient because it requires at most five additions and one multiplication for each time sample regardless of the size of the triangle smoothing radius.
To summarize, triangle smoothing is implemented in time by the following four steps in any order: (1) three-point filtering following equation 6, (2) causal integration following equation 3, (3) anti-causal integration following equation 4, and (4) division by
becomes the triangle smoothing radius, or half the number of points included in a moving average under a triangle window. The numerator in 5 is represented by the following filtering operation:
Triangle smoothing is efficient because it requires at most five additions and one multiplication for each time sample regardless of the size of the triangle smoothing radius.
To summarize, triangle smoothing is implemented in time by the following four steps in any order: (1) three-point filtering following equation 6, (2) causal integration following equation 3, (3) anti-causal integration following equation 4, and (4) division by 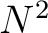 .
By expanding
.
By expanding 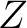 and redefining the triangle smoothing radius as
and redefining the triangle smoothing radius as  , we can redefine a triangle filter as a function of smoothing radius and frequency
In practice, smoothing with a non-integer radius is implemented using interpolation between two triangles with the nearest integer radii (Fomel, 2016).
, we can redefine a triangle filter as a function of smoothing radius and frequency
In practice, smoothing with a non-integer radius is implemented using interpolation between two triangles with the nearest integer radii (Fomel, 2016).