 |
 |
 |
 | 3D generalized nonhyperboloidal moveout approximation |  |
![[pdf]](icons/pdf.png) |
Next: Accuracy tests
Up: General method for parameter
Previous: Zero-offset ray
Suppose that each independent  -th ray corresponds to ray parameters
-th ray corresponds to ray parameters  and
and  and arrives at offset
and arrives at offset  and
and  with reflection traveltime
with reflection traveltime  . The
. The  index ranges from 1 to 4 and denotes the associated ray direction of
index ranges from 1 to 4 and denotes the associated ray direction of  -axis,
-axis,  -axis,
-axis,  , and
, and  respectively. Substituting moveout approximation 1 into equations
respectively. Substituting moveout approximation 1 into equations
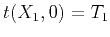 and
and
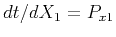 and solving for
and solving for  and
and 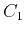 , we have, from the ray along
, we have, from the ray along  -axis (
-axis (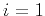 ) (Fomel and Stovas, 2010):
) (Fomel and Stovas, 2010):
Analogously,  and
and 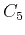 can be found from solving equations
can be found from solving equations
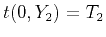 and
and
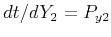 , which is equivalent to replacing
, which is equivalent to replacing 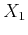 ,
, 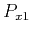 , and
, and 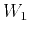 with
with 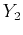 ,
,  , and
, and 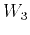 respectively in equations 15 and 16. The remaining coefficients:
respectively in equations 15 and 16. The remaining coefficients:  ,
, 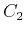 ,
, 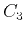 , and
, and  can be solved numerically from the four conditions given below:
can be solved numerically from the four conditions given below:
They represents matchings of  and
and  along rays in
along rays in  and
and  directions and traveltime
directions and traveltime 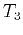 and
and 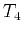 along rays in
along rays in  and
and  directions.
Provided the above information from the zero-offset ray and four finite-offset rays, we can define the remaining parameters appearing in the proposed moveout approximation (equation 1) in a systematic manner.
directions.
Provided the above information from the zero-offset ray and four finite-offset rays, we can define the remaining parameters appearing in the proposed moveout approximation (equation 1) in a systematic manner.
 |
 |
 |
 | 3D generalized nonhyperboloidal moveout approximation |  |
![[pdf]](icons/pdf.png) |
Next: Accuracy tests
Up: General method for parameter
Previous: Zero-offset ray
2017-04-20
![]() -th ray corresponds to ray parameters
-th ray corresponds to ray parameters ![]() and
and ![]() and arrives at offset
and arrives at offset ![]() and
and ![]() with reflection traveltime
with reflection traveltime ![]() . The
. The ![]() index ranges from 1 to 4 and denotes the associated ray direction of
index ranges from 1 to 4 and denotes the associated ray direction of ![]() -axis,
-axis, ![]() -axis,
-axis, ![]() , and
, and ![]() respectively. Substituting moveout approximation 1 into equations
respectively. Substituting moveout approximation 1 into equations
![]() and
and
![]() and solving for
and solving for ![]() and
and ![]() , we have, from the ray along
, we have, from the ray along ![]() -axis (
-axis (![]() ) (Fomel and Stovas, 2010):
) (Fomel and Stovas, 2010):