 |
 |
 |
 | 3D generalized nonhyperboloidal moveout approximation |  |
![[pdf]](icons/pdf.png) |
Next: Connections with other approximations
Up: Sripanich et al.: 3D
Previous: Introduction
Let  represent the two-way reflection traveltime as a function of the source-receiver offset with components
represent the two-way reflection traveltime as a function of the source-receiver offset with components  and
and  in a given acquisition coordinate frame. We propose the following general functional form of nonhyperboloidal moveout approximation (Sripanich and Fomel, 2015a):
in a given acquisition coordinate frame. We propose the following general functional form of nonhyperboloidal moveout approximation (Sripanich and Fomel, 2015a):
 |
(1) |
where
and 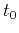 denotes the two-way traveltime at zero offset. The total number of independent parameters in equation 1 is seventeen including
denotes the two-way traveltime at zero offset. The total number of independent parameters in equation 1 is seventeen including 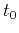 ,
, 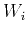 ,
,  ,
,  , and
, and 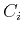 . A simple algebraic transformation of equation 1 leads to the following expression in polar coordinates:
. A simple algebraic transformation of equation 1 leads to the following expression in polar coordinates:
where
and
 represents the absolute offset and
represents the absolute offset and 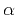 denotes the azimuthal angle from the
denotes the azimuthal angle from the  -axis. Along a fixed azimuth
-axis. Along a fixed azimuth 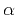 , equation 1 reduces to the generalized nonhyperbolic moveout approximation (GMA) of Fomel and Stovas (2010).
, equation 1 reduces to the generalized nonhyperbolic moveout approximation (GMA) of Fomel and Stovas (2010).
Subsections
 |
 |
 |
 | 3D generalized nonhyperboloidal moveout approximation |  |
![[pdf]](icons/pdf.png) |
Next: Connections with other approximations
Up: Sripanich et al.: 3D
Previous: Introduction
2017-04-20
![]() represent the two-way reflection traveltime as a function of the source-receiver offset with components
represent the two-way reflection traveltime as a function of the source-receiver offset with components ![]() and
and ![]() in a given acquisition coordinate frame. We propose the following general functional form of nonhyperboloidal moveout approximation (Sripanich and Fomel, 2015a):
in a given acquisition coordinate frame. We propose the following general functional form of nonhyperboloidal moveout approximation (Sripanich and Fomel, 2015a):
