On anelliptic approximations for qP velocities in TI and orthorhombic media

Muir and Dellinger Approximations

Similar to the derivations by Fomel (2004), the Muir-Dellinger approximations (Muir and Dellinger, 1985; Dellinger et al., 1993) serve as the starting point of our derivation. The Muir-Dellinger phase-velocity approximation is of the following form:

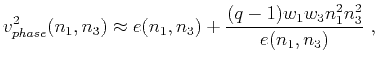$$v^2_{phase}(n_1,n_3) \approx e(n_1,n_3) + \frac{(q-1)w_1w_3n^2_{1}n^2_{3}}{e(n_1,n_3)}~, \\$$ (12)

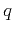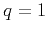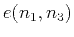where $q$ is the anelliptic parameter ($q = 1$ in case of elliptical anisotropy), $w_1=c_{11}$ denotes the horizontal ($n_1$ ) velocity squared, $w_3=c_{33}$ denotes the vertical ($n_3$ ) velocity squared, and $e(n_1,n_3)$ describes the elliptical part of the velocity and is defined by

$$e(n_1,n_3) = w_1n^2_1 + w_3n^2_3~.$$ (13)

The group-velocity approximation takes a similar form, but with symmetric changes in the coefficients and variables,

$$\frac{1}{v^2_{group}(N_1,N_3)} \approx E(N_1,N_3) + \frac{(Q-1)W_1W_3N^2_{1}N^2_{3}}{E(N_1,N_3)}~, \\$$ (14)

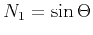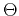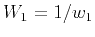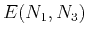where $N_1 = \sin\Theta$ , $N_3 = \cos\Theta$ , $\Theta$ is group angle (from vertical), $W_1=1/w_{1}$ denotes the horizontal slowness squared, $W_3=1/w_{3}$ denotes the vertical slowness squared, $Q = 1/q$ , and $E(N_1,N_3)$ describes the elliptical part of the slowness and is defined by

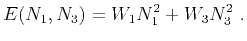$$E(N_1,N_3) = W_1N^2_1 + W_3N^2_3~.$$ (15)

As suggested by Muir and Dellinger (1985), the 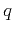$q$ parameter can be found by fitting the phase-velocity curvature around either the vertical axis ( 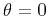$\theta = 0$ ) or the horizontal axis ( 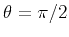$\theta = \pi/2$ ). The explicit expressions of 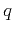$q$ fitting in those two cases are given in equations 1 and 2. If we define $Q$ in equation 14 by fitting the group velocity curvature around either $\Theta = 0$ or $\Theta = \pi/2$ , we find that

$$Q_i=1/q_i~.$$ (16)

Extending this idea, Dellinger et al. (1993) proposed four-parameter approximations for phase and group velocites using both $q_1$ and $q_3$ .

On anelliptic approximations for qP velocities in TI and orthorhombic media