 |
 |
 |
 | On anelliptic approximations for qP velocities in TI and orthorhombic media |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Proposed Approximations
Previous: Proposed Approximations
To convert the proposed group-velocity approximation (equation 47) to the corresponding moveout approximation, we apply again the general expression given in equation 31. Adopting the same notation rules, the moveout approximation takes the form:
where
 |
(55) |
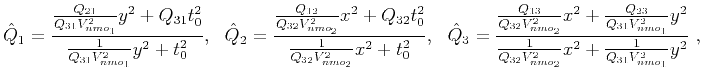 |
|
|
(56) |
 |
|
|
(57) |
 denotes the offset in
denotes the offset in  direction,
direction,  denotes the offset in
denotes the offset in  direction,
direction,
 denotes the NMO-velocity in
denotes the NMO-velocity in  direction,
direction,
 denotes the NMO-velocity in
denotes the NMO-velocity in  direction,
and
direction,
and
 denotes the hyperboloidal part of reflection traveltime squared given below,
denotes the hyperboloidal part of reflection traveltime squared given below,
 |
(58) |
We apply the same strategy to reduce the number of parameters with an approximation on  for
for  as in equation 35.
as in equation 35.
For small offset, the Taylor expansion of equation 54 is
The asymptote of this expression for unbounded offsets  and
and  is given by
is given by
 and and |
(60) |
which denote the horizontal velocities squared along  and
and  directions respectively.
directions respectively.
 |
 |
 |
 | On anelliptic approximations for qP velocities in TI and orthorhombic media |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Proposed Approximations
Previous: Proposed Approximations
2017-04-14

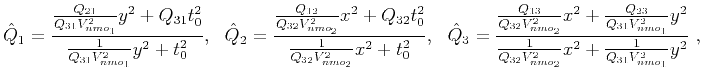






 and
and