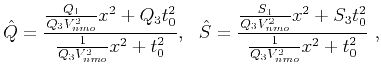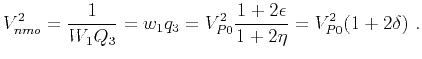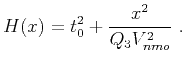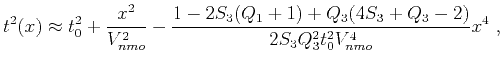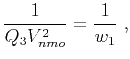next up previous On anelliptic approximations for qP velocities in TI and orthorhombic media [pdf]

Next: Examples Up: Proposed Approximations Previous: Proposed Approximations

Moveout approximation

The group-velocity approximation in equation 24 can be easily converted into the corresponding moveout equation using the relationship between offset ($ x$ ), vertical distance ($ z$ ), and total reflection traveltime ($ t$ ) given by

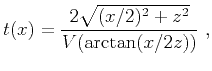$\displaystyle t(x) = \frac{2\sqrt{(x/2)^2+z^2}}{V(\arctan(x/2z))}~,$ (31)

where $ z = t_0 V(0)/2$ is the depth of the reflector, $ t_0$ is the vertical two-way reflection traveltime, and V($ \Theta $ ) is the approximated group velocity. The moveout equation corresponding to equation 24 is thus,

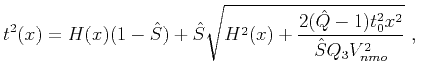$\displaystyle t^2(x) = H(x)(1-\hat{S}) + \hat{S}\sqrt{H^2(x)+\frac{2(\hat{Q}-1)t^2_0x^2}{\hat{S}Q_3V^2_{nmo}}}~,\\ $ (32)

where

$\displaystyle \hat{Q} = \frac{\frac{Q_1}{Q_3V^2_{nmo}}x^2 + Q_3t^2_0}{\frac{1}{... ...ac{\frac{S_1}{Q_3V^2_{nmo}}x^2 + S_3t^2_0}{\frac{1}{Q_3V^2_{nmo}}x^2 + t^2_0}~,$    

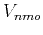$ V_{nmo}$ denotes the NMO-velocity (Alkhalifah and Tsvankin, 1995) and is given by

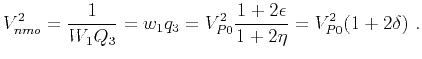$\displaystyle V^2_{nmo} = \frac{1}{W_1Q_3} = w_1 q_3 = V^2_{P0}\frac{1+2\epsilon}{1+2\eta} = V^2_{P0}(1+2\delta)~.$ (33)

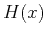$ H(x)$ denotes the hyperbolic part of the reflection traveltime squared and is given by

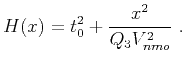$\displaystyle H(x) = t^2_0 + \frac{x^2}{Q_3V^2_{nmo}}~.$ (34)

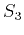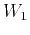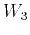Assuming a particular media type and using a linear relationship between $ q_1$ and $ q_3$ , we reduce the number of independent moveout parameters in the similar manner. However, note that $ S_1$ (equations 29) and $ S_3$ (equation 30) also depend on $ W_1$ and $ W_3$ . Therefore, to effectively reduce the number of parameters in the moveout approximation (equation 32) to three, we suggest, as an approximation, to adopt 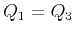$ Q_1 = Q_3$ only for equations 29 and 30, which lead to

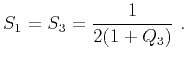$\displaystyle S_1 = S_3 = \frac{1}{2(1+Q_3)}~.$ (35)

As a result, the moveout approximation depends on 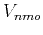$ t_0$ , $ V_{nmo}$ , and $ Q_3$ .

For small offsets, the Taylor expansion of equation 32 is

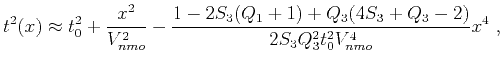$\displaystyle t^2(x) \approx t^2_0 +\frac{x^2}{V^2_{nmo}} -\frac{1-2S_3(Q_1+1)+Q_3(4S_3+Q_3-2)}{2S_3Q_3^2t_0^2V^4_{nmo}} x^4 ~,$ (36)

which reduces to the expression given by Fomel (2004) by setting 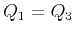$ Q_1 = Q_3$ . The asymptote of this expression for unbounded offset $ x$ is given by

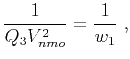$\displaystyle \frac{1}{Q_3 V^2_{nmo}} = \frac{1}{w_1}~,$ (37)

which is the horizontal velocity squared.

In the Muir-Dellinger notation, another nonhyperbolic moveout approximation, the generalized nonhyperbolic moveout approximation (Stovas, 2010; Fomel and Stovas, 2010) can be expressed as

$\displaystyle t^2(x)$ $\displaystyle \approx$ $\displaystyle t_0^2 + \frac{x^2}{V^2_{nmo}} + \frac{Ax^4}{V^4_{nmo}\left(t_0^2 ... ...o}}+\sqrt{t_0^4+2Bt_0^2\frac{x^2}{V^2_{nmo}}+C\frac{x^4}{V^4_{nmo}}} \right)}~,$ (38)
$\displaystyle A$ $\displaystyle =$ $\displaystyle \frac{(Q_3-1)^2 (Q_1 W_3-Q_3 W_1)}{Q_3(Q_1-1) (W_1-W_3)}~,$  
$\displaystyle B$ $\displaystyle =$ $\displaystyle \frac{(Q_3-1) \left[\left(2 Q_3^2-1\right) W_1+W_3-2 Q_1 Q_3 W_3\right]}{Q_3(Q_1-1) (W_1-W_3)}~,$  
$\displaystyle C$ $\displaystyle =$ $\displaystyle \frac{(Q_3-1)^2}{(Q_1-1)^2 Q_3^2}~.$  

If the empirical assumption of 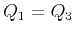$ Q_1 = Q_3$ , or equivalently acoustic approximation is used, equation 38 reduces to the moveout approximation of Fomel (2004).

next up previous On anelliptic approximations for qP velocities in TI and orthorhombic media [pdf]

Next: Examples Up: Proposed Approximations Previous: Proposed Approximations

2017-04-14