|
|
|
|
Elastic wave-vector decomposition in heterogeneous anisotropic media |
 is given in equation 16.
is given in equation 16.
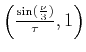 min
min denotes the modified version of
denotes the modified version of
 in places where the given phase direction
in places where the given phase direction



|
|---|
|
orthos02,orthos01,orthos005
Figure 6. Weight |
|
|
|
|
|
|
Elastic wave-vector decomposition in heterogeneous anisotropic media |