|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Taking heterogeneity into account Up: Traveltime in general 2-D Previous: Traveltime in general 2-D
To understand how the contribution from each sublayer influences the desired second-order traveltime derivative at the surface, we follow the notion of Blias (1981), Blyas et al. (1984), Gritsenko (1984), and Goldin (1986) and establish the connections between the second-order traveltime derivatives evaluated at different interfaces using the Fermat's principle, which states that the total traveltime 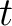 has to be stationary with respect to
has to be stationary with respect to 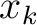 for
for
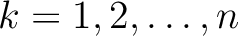 , leading to
, leading to
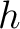 , which gives
where
, which gives
where 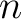 is the index for the topmost layer. Due to the Fermat’s condition in equation 8, we then have
Further differentiating equation 10 with respect to
is the index for the topmost layer. Due to the Fermat’s condition in equation 8, we then have
Further differentiating equation 10 with respect to 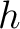 , we arrive at
which can be used to compute the desired second-order traveltime derivative (
, we arrive at
which can be used to compute the desired second-order traveltime derivative (
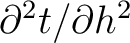 ). In Appendix B, we show that by differentiating the Fermat’s condition in equation 8, the quantity
). In Appendix B, we show that by differentiating the Fermat’s condition in equation 8, the quantity 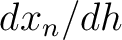 in equation 11 can be computed from the following recursive formula:
with
in equation 11 can be computed from the following recursive formula:
with
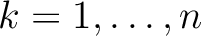 . Note that because
. Note that because
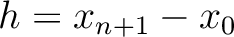 and
and 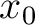 is independent of
is independent of 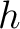 by definition,
by definition,
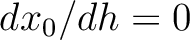 and
and
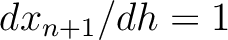 , which lead to
, which lead to 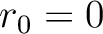 and
and
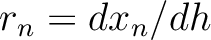 . Equations 11 and 12 suggest that the desired second-order traveltime derivative at the surface can be computed by collecting the contributions from derivatives on
. Equations 11 and 12 suggest that the desired second-order traveltime derivative at the surface can be computed by collecting the contributions from derivatives on 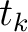 from different sublayers through a recursion. The general results for multi-layer media in equations 11 and 12 represent a direct extension of the original findings for two-layer media by Blias (1981), Blyas et al. (1984), Gritsenko (1984), and Goldin (1986). Previously, only the two-layer version of this recursion was adopted and an approximate summation of contributions rather than a recursion was used. We review this proposition in Appendix C and discuss some connections to the exact recursion studied here.
from different sublayers through a recursion. The general results for multi-layer media in equations 11 and 12 represent a direct extension of the original findings for two-layer media by Blias (1981), Blyas et al. (1984), Gritsenko (1984), and Goldin (1986). Previously, only the two-layer version of this recursion was adopted and an approximate summation of contributions rather than a recursion was used. We review this proposition in Appendix C and discuss some connections to the exact recursion studied here.
Equations 11 and 12 represent a framework for computing the desired second-order total one-way traveltime derivative at the surface (
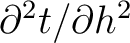 ) from second-order one-way traveltime derivatives corresponding to different sublayers (
) from second-order one-way traveltime derivatives corresponding to different sublayers (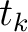 ). In the next section, we introduce lateral heterogeneity effects for interfaces
). In the next section, we introduce lateral heterogeneity effects for interfaces 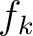 and the group slowness
and the group slowness 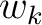 to the traveltime in each sublayer
to the traveltime in each sublayer 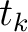 in equation 4. We subsequently compute the derivatives on
in equation 4. We subsequently compute the derivatives on 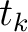 that include both effects, which can then be used by recursion 12.
that include both effects, which can then be used by recursion 12.