|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Diffraction traveltime Up: Appendix A Review of Previous: Appendix A Review of
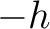 and
and 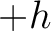 ) as follows (Thomsen, 2014; Sripanich and Fomel, 2016; Tsvankin, 2012):
We follow the same notation as in the main text and use
) as follows (Thomsen, 2014; Sripanich and Fomel, 2016; Tsvankin, 2012):
We follow the same notation as in the main text and use  to denote one-way zero-offset traveltime. Equation (27) can be converted to a more commonly known series in two-way traveltime squared in terms of full offsets (
to denote one-way zero-offset traveltime. Equation (27) can be converted to a more commonly known series in two-way traveltime squared in terms of full offsets (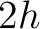 ) as follows:
where
) as follows:
where 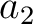 and
and 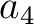 are coefficients related to the NMO velocity and the quartic coefficient, respectively. Both parameters can be expressed in terms of the derivative of one-way traveltime around zero offset as follows (Al-Dajani and Tsvankin, 1998; Sripanich and Fomel, 2016):
are coefficients related to the NMO velocity and the quartic coefficient, respectively. Both parameters can be expressed in terms of the derivative of one-way traveltime around zero offset as follows (Al-Dajani and Tsvankin, 1998; Sripanich and Fomel, 2016):
We emphasize that two important assumptions are made in the derivation so far:
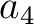 ) becomes more complex than what is shown in equation (30) (Koren and Ravve, 2017; Pech et al., 2003). Grechka and Tsvankin (1998) emphasized that reflection dispersal has no effect on NMO velocity related to equation (29) (Hubral and Krey, 1980). It becomes important only when considering higher-order traveltime coefficients such as
) becomes more complex than what is shown in equation (30) (Koren and Ravve, 2017; Pech et al., 2003). Grechka and Tsvankin (1998) emphasized that reflection dispersal has no effect on NMO velocity related to equation (29) (Hubral and Krey, 1980). It becomes important only when considering higher-order traveltime coefficients such as 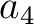 in equation (30).
in equation (30).
In this paper, we only utilize the relationship between the reflection traveltime coefficients (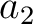 ) and the second-order derivative of the one-way traveltime of the fictional normal-incidence ray in equation (29), which is not affected by reflection dispersal. Therefore, NMO velocity can be computed from
) and the second-order derivative of the one-way traveltime of the fictional normal-incidence ray in equation (29), which is not affected by reflection dispersal. Therefore, NMO velocity can be computed from
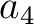 .
.