 |
 |
 |
 | Traveltime computation with
the linearized eikonal equation |  |
![[pdf]](icons/pdf.png) |
Next: ALGORITHM
Up: Fomel: Linearized Eikonal
Previous: INTRODUCTION
The eikonal equation, describing the traveltime propagation in an
isotropic medium, has the form
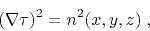 |
(1) |
where 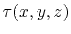 is the traveltime (eikonal) from the source to
the point with the coordinates
is the traveltime (eikonal) from the source to
the point with the coordinates 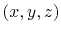 , and
, and  is the slowness at
that point (the velocity
is the slowness at
that point (the velocity 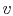 equals
equals  .) In Appendix A, I review a
basic derivation of the eikonal and transport equations. To formulate
a well-posed initial-value problem on equation (1), it is
sufficient to specify
.) In Appendix A, I review a
basic derivation of the eikonal and transport equations. To formulate
a well-posed initial-value problem on equation (1), it is
sufficient to specify 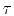 at some closed surface and to choose one
of the two branches of the solution (the wave going from or to the
source.)
at some closed surface and to choose one
of the two branches of the solution (the wave going from or to the
source.)
Equation (1) is nonlinear. The nonlinearity is essential for
producing multiple branches of the solution. Multi-valued eikonal
solutions can include different types of waves (direct, reflected,
diffracted, head, etc.) as well as different branches of caustics. To
linearize equation (1), we need to assume that an initial
estimate  of the eikonal
of the eikonal 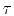 is available. The traveltime
is available. The traveltime
 corresponds to some slowness
corresponds to some slowness  , which can be computed
from equation (1) as
, which can be computed
from equation (1) as
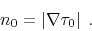 |
(2) |
Let us denote the residual traveltime 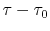 by
by  and
the residual slowness
and
the residual slowness 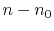 by
by  . With these definitions, we
can rewrite equation (1) in the form
. With these definitions, we
can rewrite equation (1) in the form
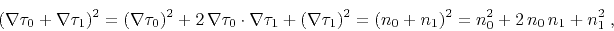 |
(3) |
or, taking into account equality (2),
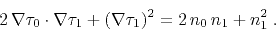 |
(4) |
Neglecting the squared terms, we arrive at the equation
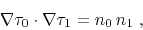 |
(5) |
which is the linearized version of the eikonal equation (1).
The accuracy of the linearization depends on the relative ratio of the
slowness perturbation  and the true slowness model
and the true slowness model  . Though it
is difficult to give a quantitative estimate, the ratio of 10% is
generally assumed to be a safe upper bound.
. Though it
is difficult to give a quantitative estimate, the ratio of 10% is
generally assumed to be a safe upper bound.
The intimate connection of the linearized eikonal equation
and traveltime tomography is discussed in Appendix B.
 |
 |
 |
 | Traveltime computation with
the linearized eikonal equation |  |
![[pdf]](icons/pdf.png) |
Next: ALGORITHM
Up: Fomel: Linearized Eikonal
Previous: INTRODUCTION
2013-03-03
![]() of the eikonal
of the eikonal ![]() is available. The traveltime
is available. The traveltime
![]() corresponds to some slowness
corresponds to some slowness ![]() , which can be computed
from equation (1) as
, which can be computed
from equation (1) as