Exploring three-dimensional implicit wavefield extrapolation with the helix transform

Bibliography

Alkhalifah, T., and S. Fomel, 1997, Residual migration in VTI media using anisotropy continuation, in SEP-94: Stanford Exploration Project, 327-337.

Baker, G. A., and P. Graves-Morris, 1981, Padé approximants: Addison-Wesley.

Biondi, B., 1996, Common-azimuth prestack depth migration of a North Sea data set, in SEP-93: Stanford Exploration Project, 1-14.

Biondi, B., and G. Palacharla, 1993, 3-D wavefield depth extrapolation by rotated McClellan filters, in SEP-77: Stanford Exploration Project, 27-36.

----, 1994, 3-D prestack migration of common-azimuth data, in SEP-80: Stanford Exploration Project, 109-124.

Birkhoff, G., 1971, The numerical solution of elliptic equations: SIAM.

Claerbout, J., 1997a, Multidimensional recursive filters via a helix, in SEP-95: Stanford Exploration Project, 1-13.

Claerbout, J. F., 1976, Fundamentals of geophysical data processing: Blackwell.

----, 1985, Imaging the Earth's Interior: Blackwell Scientific Publications.

----, 1986, Velocity extrapolation by cascaded 15 degree migration, in SEP-48: Stanford Exploration Project, 79-84.

----, 1992, Earth Soundings Analysis: Processing Versus Inversion: Blackwell Scientific Publications.

----, 1997b, Geophysical exploration mapping: Environmental soundings image enhancement: Stanford Exploration Project.

Cole, J. B., 1994, A nearly exact second-order finite-difference time-domain wave propagation algorithm on a coarse grid: Computers in Physics, 8.

Crank, J., and P. Nicolson, 1947, A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type: Proceedings of the Cambridge Philosophical Society, 43, 50-67.

Etgen, J. T. E., 1994, Stability of explicit depth extrapolation through laterally-varying media: 64th Ann. Internat. Mtg, Soc. of Expl. Geophys., 1266-1269.

Fomel, S., 1995, Amplitude preserving offset continuation in theory Part 1: The offset continuation equation, in SEP-84: Stanford Exploration Project, 179-198.

----, 1996a, Migration and velocity analysis by velocity continuation, in SEP-92: Stanford Exploration Project, 159-188.

----, 1996b, Stacking operators: Adjoint versus asymptotic inverse, in SEP-92: Stanford Exploration Project, 267-292.

Fomel, S. B., 1994, Method of velocity continuation in the problem of seismic time migration: Russian Geology and Geophysics, 35, 100-111.

Gazdag, J., 1978, Wave equation migration with the phase-shift method: Geophysics, 43, 1342-1351.

Godfrey, R. J., F. Muir, and J. F. Claerbout, 1979, Stable extrapolation, in SEP-16: Stanford Exploration Project, 83-87.

Hale, D., 1991a, 3-D depth migration via McClellan transformations: Geophysics, 56, 1778-1785.

(Erratum in GEO-57-2-370).

----, 1991b, Stable explicit depth extrapolation of seismic wavefields: Geophysics, 56, 1770-1777.

Holberg, O., 1988, Towards optimum one-way wave propagation: Geophys. Prosp., 36, 99-114.

Kolmogorov, A. N., 1939, Sur l'interpolation et l'extrapolation des suites stationnairres: C.R. Acad.Sci., 208, 2043-2045.

Krail, P. M., 1993, Sub-salt acquisition with a vertical cable: 63rd Ann. Internat. Mtg, Soc. of Expl. Geophys., 1376.

(Imaging Sedimentary Structures under Salt Research Workshop).

Li, Z., 1986, Cascaded one step fifteen degree migration versus Stolt migration, in SEP-48: Stanford Exploration Project, 85 -100.

McClellan, J. H., 1973, The design of two-dimensional digital filters by transformations: 7th Annual Princeton Conf. on Inform. Sci. and Syst., Proceedings, 247-251.

Nichols, D., 1991, Three-dimensional depth migration by a predictor corrector method, in SEP-70: Stanford Exploration Project, 31-38.

Vetterli, M., and J. Kovacevic, 1995, Wavelets and subband coding: Prentice Hall.

Appendix A

The 1/6-th trick

Given the filter $D_2 (k)$, defined in formula (10), we can construct an accurate approximation to the second derivative operator $-k^2$ by considering a filter ratio (another Padé-type approximation) of the form

$$-k^2 \approx \frac{D_2(k)}{1 + \beta D_2 (k)}\;,$$ (25)

where $\beta$ is an adjustable constant (Claerbout, 1985). The actual Padé coefficient is $\beta=1/12$. As pointed out by Francis Muir, the value of $\beta = 1/4 - 1/\pi^2 \approx 1/6.726$ gives an exact fit at the Nyquist frequency $k = \pi$. Fitting the derivative operator in the $L_1$ norm yields the value of $\beta \approx 1/8.13$. All these approximations are shown in Figure A-1.

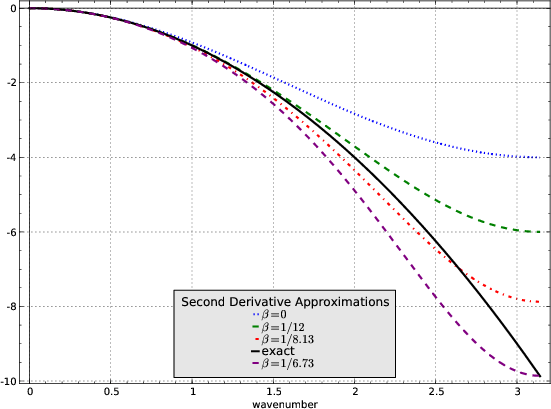
sixth Figure A-1. The second-derivative operator in the wavenumber domain and its approximations.

Appendix B

Constructing an ``isotropic'' Laplacian operator

The problem of approximating the Laplacian operator in two dimensions not only inherits the inaccuracies of the one-dimensional finite-difference approximations, but also raises the issue of azimuthal asymmetry. For example, the usual five-point filter

$$F_5 = \begin{array}{\vert r\vert r\vert r\vert} \hline 0 & 1... ...\\ \hline 1 & -4 & 1 \\ \hline 0 & 1 & 0 \\ \hline \end{array}$$ (26)

exhibits a clear difference between the grid directions and the directions at a 45-degree angle to the grid. To overcome this unpleasant anisotropy, we can consider a slightly larger filter of the form

$$F_9 = \begin{array}{\vert r\vert r\vert r\vert} \hline \alph... ...gamma \\ \hline \alpha & \gamma & \alpha \\ \hline \end{array}$$ (27)

where the constants $\alpha$ and $\gamma$ are to be defined. The Fourier-domain representation of filter (B-2) is

$$F_9 (k_x,k_y) = 4\,\alpha\,[\cos{k_x}\,\cos{k_y} - 1] + 2\,\gamma\,[\cos{k_x}+\cos{k_y}-2]\;,$$ (28)

and the isotropic filter that we can try to approximate is defined analogously to its one-dimensional equivalent, as follows:

$$F (k_x,k_y) = 2 (\cos{k} -1) = 2 (\cos{\sqrt{k_x^2+k_y^2}} - 1)\;.$$ (29)

Comparing equations (B-3) and (B-4), we notice that they match exactly, when either of the wavenumbers $k_x$ or $k_y$ is equal to zero, provided that

$$\alpha = \frac{1-\gamma}{2}\;.$$ (30)

Therefore, we can reduce the problem to estimating a single coefficient $\gamma$. Another way of expressing this conclusion is to represent filter $F_9$ in equation (B-3) as a linear combination of filter $F_5$ from equation (B-3) and its rotated version (Cole, 1994), as follows:

$$F_9 = \gamma\, \begin{array}{\vert r\vert r\vert r\vert} \h... ...hline 0 & -2 & 0 \\ \hline 1/2 & 0 & 1/2 \\ \hline \end{array}$$ (31)

With the value of $\gamma=0.5$, filter $F_9$ takes the value

$$F_9 = \begin{array}{\vert r\vert r\vert r\vert} \hline 1/4 &... ...1/2 & -3 & 1/2 \\ \hline 1/4 & 1/2 & 1/4 \\ \hline \end{array}$$ (32)

and corresponds precisely to the nine-point McClellan filter (Hale, 1991a; McClellan, 1973). On the other hand, the value of $\gamma =2/3$ gives the least error in the vicinity of the zero wavenumber $k$. In this case, the filter is

$$F_9 = \begin{array}{\vert r\vert r\vert r\vert} \hline 1/6 &... ... & -10/3 & 2/3 \\ \hline 1/6 & 2/3 & 1/6 \\ \hline \end{array}$$ (33)

Errors of different approximations are plotted in Figure B-1

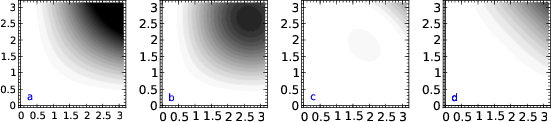
laplace
Figure B-1. The numerical anisotropy error of different Laplacian approximations. Both the five-point Laplacian (plot a) and its rotated version (plot b) are accurate along the axes, but exhibit significant anisotropy in between at large wavenumbers. The nine-point McClellan filter (plot c) has a reduced error, while the filter with $\gamma =2/3$ (plot d) has the flattest error around the origin.

Under the helix transform, a filter of the general form (B-2) becomes equivalent to a one-dimensional filter with the $Z$ transform

$$F_9 (Z) = \alpha\,Z^{-N_x-1} + \gamma\,Z^{-N_x} + \alpha\,Z^{-N_x+1} + \gamma\,Z^{-1} -4\,(\alpha + \gamma)$$

$$+ \gamma\,Z + \alpha\,Z^{N_x-1} + \gamma\,Z^{N_x} + \alpha\,Z^{N_x+1}\;,$$ (34)

where $N_x$ is the helix period (the number of grid points in the $x$ dimension). To find the inverse of a convolution with filter (B-9), we factorize the filter into the causal minimum-phase component and its adjoint:

$$F_9 (Z) = P (Z) P (1/Z)\;.$$ (35)

To find the coefficients of the filter $P$, any one-dimensional spectral factorization method can be applied. It is important to point out that the result of factorization (neglecting the numerical errors) does not depend on $N_x$. Another approach is to define a residual error vector for the coefficients of Z in equation (B-10) and minimize it for some particular norm. For example, minimizing the $\mathcal{L}_1$ norm when $F_9$ is the McClellan filter (B-7), we discover that the filter $P$, after transforming back to two dimensions, takes the form

$$\begin{array}{\vert r\vert r\vert r\vert r\vert r\vert r\ver... ...3 & 0.0808 & 0.2543 & 0.3521 & 0.1553 & & \\ \hline \end{array}$$ (36)

The results of applying a recursive deconvolution with filter (B-11) are shown in Figure B-2. An essentially similar procedure, only with a different set of filters, works for implicit wavefield extrapolation.

inv-laplace
Figure B-2. Inverting the Laplacian operator by a helix deconvolution. The top left plot shows the input, which contains a single spike and the causal minimum-phase filter $P$. The top right plot is the result of inverse filtering. As expected, the filter is deconvolved into a spike, and the spike turns into a smooth one-sided impulse. After the second run, in the backward (adjoint) direction, we obtain a numerical solution of Laplace's equation! In the two bottom plots, the solution is shown with grayscale and contours.

Exploring three-dimensional implicit wavefield extrapolation with the helix transform