 |
 |
 |
 | Shaping regularization in geophysical estimation problems |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Fomel: Shaping regularization
Previous: Acknowledgments
-
Bube, K., and R. Langan, 1999, On a continuation approach to regularization
for crosswell tomography: 69th Ann. Internat. Mtg, Soc. of Expl. Geophys.,
1295-1298.
-
-
Claerbout, J., and M. Brown, 1999, Two-dimensional textures and
prediction-error filters: 61st Mtg., Eur. Assn. Geosci. Eng., Session:1009.
-
-
Claerbout, J. F., 1992, Earth Soundings Analysis: Processing Versus
Inversion: Blackwell Scientific Publications.
-
-
----, 2006, Basic Earth imaging: Stanford Exploration Project,
http://sepwww.stanford.edu/sep/prof/.
-
-
Clapp, R. G., B. Biondi, and J. F. Claerbout, 2004, Incorporating geologic
information into reflection tomography: Geophysics, 69, 533-546.
-
-
Clapp, R. G., B. L. Biondi, S. B. Fomel, and J. F. Claerbout, 1998,
Regularizing velocity estimation using geologic dip information: 68th Ann.
Internat. Mtg, Soc. of Expl. Geophys., 1851-1854.
-
-
Dix, C. H., 1955, Seismic velocities from surface measurements: Geophysics,
20, 68-86.
-
-
Engl, H., M. Hanke, and A. Neubauer, 1996, Regularization of inverse problems:
Kluwer Academic Publishers.
-
-
Fomel, S., 2002, Applications of plane-wave destruction filters: Geophysics,
67, 1946-1960.
-
-
----, 2003, Time-migration velocity analysis by velocity continuation:
Geophysics, 68, 1662-1672.
-
-
Fomel, S., and J. Claerbout, 2003, Multidimensional recursive filter
preconditioning in geophysical estimation problems: Geophysics, 68,
577-588.
-
-
Fomel, S., and A. Guitton, 2006, Regularizing seismic inverse problems by
model re-parameterization using plane-wave construction: Geophysics, 71, S209-S217.
-
-
Fomel, S., P. Sava, J. Rickett, and J. Claerbout, 2003, The Wilson-Burg
method of spectral factorization with application to helical filtering:
Geophysical Prospecting, 51, 409-420.
-
-
Harlan, W. S., 1995, Regularization by model redefinition:
http://billharlan.com/pub/papers/regularization.pdf.
-
-
Hestenes, M. R., and E. Steifel, 1952, Methods of conjugate gradients for
solving linear systems: J. Res. Nat. Bur. Stand., 49, 409-436.
-
-
Jackson, D. D., 1972, Interpretation of inaccurate, insufficient and
inconsistent data: Geophys. J. R. Astron. Soc., 28, 97-109.
-
-
Liu, B., and M. Sacchi, 2001, Minimum weighted norm interpolation of seismic
data with adaptive weights: 71st Ann. Internat. Mtg, Soc. of Expl. Geophys.,
1921-1924.
-
-
Portniaguine, O., and J. Castagna, 2004, Inverse spectral decomposition, in 74th Ann. Internat. Mtg: Soc. of Expl. Geophys., 1786-1789.
-
-
Saad, Y., 2003, Iterative methods for sparse linear systems: SIAM.
-
-
Sinoquet, D., 1993, Modeling a priori information on the velocity field in
reflection tomography: 63rd Ann. Internat. Mtg, Soc. of Expl. Geophys.,
591-594.
-
-
Tarantola, A., 2004, Inverse problem theory and methods for model parameter
estimation: SIAM.
-
-
Tikhonov, A. N., 1963, Solution of incorrectly formulated problems and the
regularization method: Sovet Math. Dokl., 1035-1038.
-
-
Trad, D., T. Ulrych, and M. Sacchi, 2003, Latest views of the sparse Radon
transform: Geophysics, 68, 386-399.
-
-
Valenciano, A. A., M. Brown, A. Guitton, and M. D. Sacchi, 2004, Interval
velocity estimation using edge-preserving regularization, in 74th Ann.
Internat. Mtg: Soc. of Expl. Geophys.
-
-
van der Vorst, H. A., 2003, Iterative Krylov methods for large linear
systems: Cambridge University Press.
-
-
Versteeg, R., and W. W. Symes, 1993, Geometric constraints on seismic
inversion: 63rd Ann. Internat. Mtg, Soc. of Expl. Geophys., 595-598.
-
-
Woodward, M. J., P. Farmer, D. Nichols, and S. Charles, 1998, Automated 3-D
tomographic velocity analysis of residual moveout in prestack depth migrated
common image point gathers: 68th Ann. Internat. Mtg, Soc. of Expl. Geophys.,
1218-1221.
-
-
Zhdanov, M. S., 2002, Geophysical inverse theory and regularization problems:
Elsevier Science.
-
-
Zhou, H., S. Gray, J. Young, D. Pham, and Y. Zhang, 2003, Tomographic residual
curvature analysis: The process and its components: 73rd Ann. Internat.
Mtg., Soc. of Expl. Geophys., 666-669.
-
Appendix
A
Conjugate-gradient algorithm
A complete algorithm for conjugate-gradient iterative inversion with
shaping regularization is given below. The algorithm follows directly
from combining equation 13 with the classic
conjugate-gradient algorithm of Hestenes and Steifel (1952).
![\begin{algorithm}{Conjugate gradients with shaping}{\mathbf{L},\mathbf{H},\mathb...
...ight] \\
\hat{\rho} \= \rho
\end{FOR} \\
\RETURN \mathbf{m}
\end{algorithm}](img60.png)
The iteration terminates after 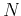 iterations or upon reaching convergence
to the specified tolerance
iterations or upon reaching convergence
to the specified tolerance  . It uses auxiliary vectors
. It uses auxiliary vectors  ,
,
 ,
,  ,
, 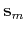 ,
, 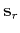 ,
, 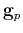 ,
,
 ,
,  and applies operators
and applies operators  ,
,
 and their adjoints only once per each iteration.
and their adjoints only once per each iteration.
Appendix
B
Combining shaping operators
General rules can be developed to combine two or more shaping operators for
the cases when there are several features in the model that need to be
characterized simultaneously. A general rule for combining two different
shaping operators  and
and  can have the form
can have the form
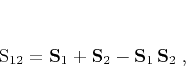 |
(21) |
where one adds the responses of the two shapers and then subtracts
their overlap. An example is shown in Figure B-1, where
an impulse response for oriented smoothing in two different directions
is constructing from smoothing in each of the two directions
separately.
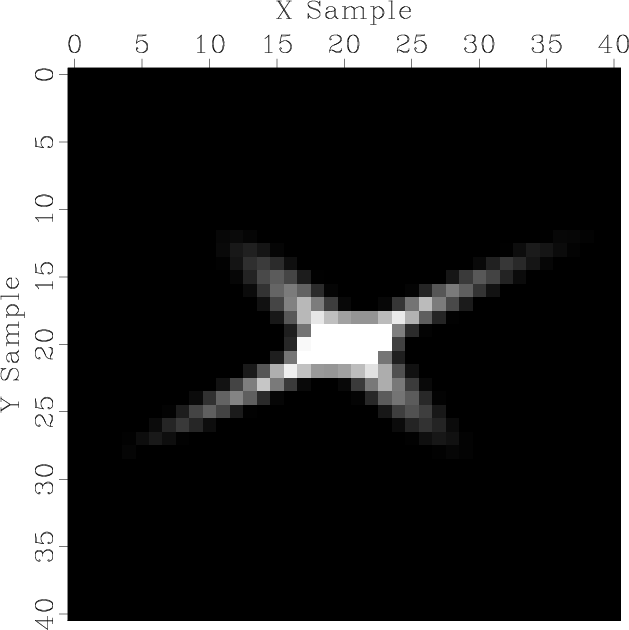
test12
Figure B-1. Impulse response for a
combination of two shaping operators smoothing in two different
directions.
|
|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
Combining two operators that work in orthogonal directions can be
accomplished with a simple tensor product, as follows:
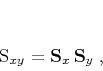 |
(22) |
where
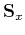 and
and
 are shaping operators that apply
in orthogonal
are shaping operators that apply
in orthogonal  - and
- and  -directions, and
-directions, and
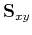 is a combined
operator that works in both directions. An example is shown in
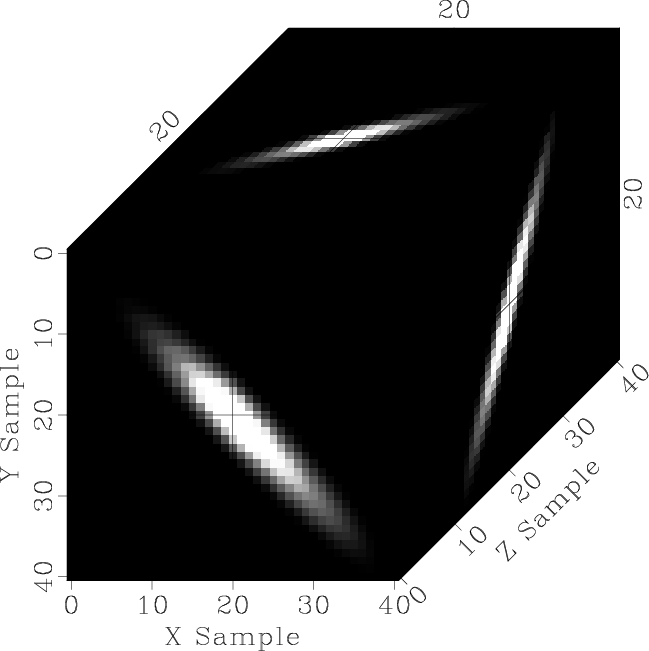
Figure B-2, where two two-dimensional shapers working in
orthogonal directions are combined to produce an impulse response of 3-D
shaping operator that applies smoothing along a three-dimensional plane.
is a combined
operator that works in both directions. An example is shown in
Figure B-2, where two two-dimensional shapers working in
orthogonal directions are combined to produce an impulse response of 3-D
shaping operator that applies smoothing along a three-dimensional plane.
plane
Figure B-2. 3-D impulse response for a
combination of two 2-D shaping operators smoothing in in-line and
cross-line directions.
|
|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
Constructing multidimensional recursive filters for helical
preconditioning (Fomel and Claerbout, 2003) is significantly more
difficult. It involves helical spectral factorization, which may
create long inefficient filters (Fomel et al., 2003).
 |
 |
 |
 | Shaping regularization in geophysical estimation problems |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Fomel: Shaping regularization
Previous: Acknowledgments
2013-03-02
![\begin{algorithm}{Conjugate gradients with shaping}{\mathbf{L},\mathbf{H},\mathb...
...ight] \\
\hat{\rho} \= \rho
\end{FOR} \\
\RETURN \mathbf{m}
\end{algorithm}](img60.png)
![]() iterations or upon reaching convergence
to the specified tolerance
iterations or upon reaching convergence
to the specified tolerance ![]() . It uses auxiliary vectors
. It uses auxiliary vectors ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() and applies operators
and applies operators ![]() ,
,
![]() and their adjoints only once per each iteration.
and their adjoints only once per each iteration.
![]() and
and ![]() can have the form
can have the form

