 |
 |
 |
 | Modeling of pseudo-acoustic P-waves in orthorhombic media with a lowrank approximation |  |
![[pdf]](icons/pdf.png) |
Next: Dispersion Relation for Orthorhombic
Up: Theory
Previous: Theory
The acoustic wave equation is widely used in
forward seismic modeling and reverse-time migration (Bednar, 2005; Etgen et al., 2009):
 |
(1) |
where
 is the seismic pressure wavefield
and
is the seismic pressure wavefield
and  is the wave propagation velocity.
is the wave propagation velocity.
Assuming the model is homogeneous
 ,
after a Fourier transform in space,
we get the following explicit expression in the wavenumber domain:
,
after a Fourier transform in space,
we get the following explicit expression in the wavenumber domain:
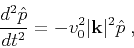 |
(2) |
where
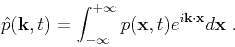 |
(3) |
Equation 2 has the following analytical solution:
 |
(4) |
which leads to
the well-known second-order time-marching scheme (Etgen, 1989; Soubaras and Zhang, 2008) :
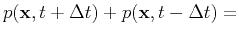 |
| |
|
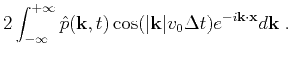 |
(5) |
Equation 5 provides a very accurate and efficient solution
in the case of a constant-velocity medium with the aid of FFTs.
When the seismic wave velocity varies in the medium,
equation 5 turns into a reasonable approximation by replacing  with
with  , and taking small time steps,
, and taking small time steps,  .
However, FFTs can no longer be applied directly to evaluate
the inverse Fourier transform,
because a space-wavenumber mixed-domain term appears in the integral operation:
.
However, FFTs can no longer be applied directly to evaluate
the inverse Fourier transform,
because a space-wavenumber mixed-domain term appears in the integral operation:
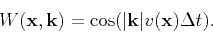 |
(6) |
As a result, a straightforward numerical implementation of wave extrapolation
in a variable velocity medium with mixed-domain
matrix 6 will increase the cost from 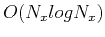 to
to  ,
the original cost for the homogeneous case,
in which
,
the original cost for the homogeneous case,
in which  is the total size of the three-dimensional space grid.
A number of numerical methods (Fomel et al., 2010; Du et al., 2010; Song et al., 2013,2011; Song and Fomel, 2011; Etgen and Brandsberg-Dahl, 2009; Liu et al., 2009; Zhang and Zhang, 2009; Fomel et al., 2012)
have been proposed to overcome this mixed-domain problem.
is the total size of the three-dimensional space grid.
A number of numerical methods (Fomel et al., 2010; Du et al., 2010; Song et al., 2013,2011; Song and Fomel, 2011; Etgen and Brandsberg-Dahl, 2009; Liu et al., 2009; Zhang and Zhang, 2009; Fomel et al., 2012)
have been proposed to overcome this mixed-domain problem.
In the case of orthorhombic acoustic modeling,
we derive a new phase operator
 to replace
to replace
 of the isotropic model.
We describe the details in the next section.
of the isotropic model.
We describe the details in the next section.
 |
 |
 |
 | Modeling of pseudo-acoustic P-waves in orthorhombic media with a lowrank approximation |  |
![[pdf]](icons/pdf.png) |
Next: Dispersion Relation for Orthorhombic
Up: Theory
Previous: Theory
2013-06-25
![]() ,
after a Fourier transform in space,
we get the following explicit expression in the wavenumber domain:
,
after a Fourier transform in space,
we get the following explicit expression in the wavenumber domain:
![]() with
with ![]() , and taking small time steps,
, and taking small time steps, ![]() .
However, FFTs can no longer be applied directly to evaluate
the inverse Fourier transform,
because a space-wavenumber mixed-domain term appears in the integral operation:
.
However, FFTs can no longer be applied directly to evaluate
the inverse Fourier transform,
because a space-wavenumber mixed-domain term appears in the integral operation:
![]() to replace
to replace
![]() of the isotropic model.
We describe the details in the next section.
of the isotropic model.
We describe the details in the next section.