Fast Multicomponent Data Registration

Multicomponent seismic data registration is an important step before quantitative seismic data interpretation and joint amplitude versus offset (AVO) analysis (Lu et al., 2015; Gao and Sacchi, 2018). The time-frequency transform is suitable for nonstationary registration of multicomponent images in frequency domain (Liu and Fomel, 2013; Chen, 2021). The main idea is to match the spectra of compressional (PP) and shear (SS) reflections to that of Ricker wavelets, making the balanced PP and SS images share a similar spectral content. Then one can squeeze the SS image and make PP and SS images display in the same coordinate system. Fig.13a and 13b shows the PP and SS images from a nine-component land survey, respectively. The interleaved image (where the PP and SS traces are interleaved one by one) of the raw PP and PS data shows the obviously discontinuous reflectors (see Fig.14a). We use the LTF decomposition as a reference comparison with the proposed SLTFT method. Fig.14b and 15 shows the interleaved images after the registration by using the LTF decompostion and the SLTFT ( 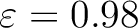$\varepsilon=0.98$), respectively. Both the LTF decomposition and the SLTFT method create the results with spatially coherent registration and high resolution, especially at the locations of the rectangle boxes. In terms of computational cost, the proposed method provides a more efficient time-frequency representation (see Table. 2), which makes it more suitable in high-dimensional field data processing tasks.

pp,ss
Figure 13. (a) PP and (b) SS images from a multicomponent land survey.

before,after
Figure 14. The interleaved image of (a) raw data, after registration by using (b) LTF decomposition.

after1
Figure 15. The interleaved image after registration by using SLTFT.

Table 2: Comparison of Time Consumptions.$^1$