|
|
|
|
Fast Streaming Local Time-frequency Transform for Nonstationary Seismic Data Processing |
Next: Fast Inverse-Q Filtering in Up: Applications Previous: Applications
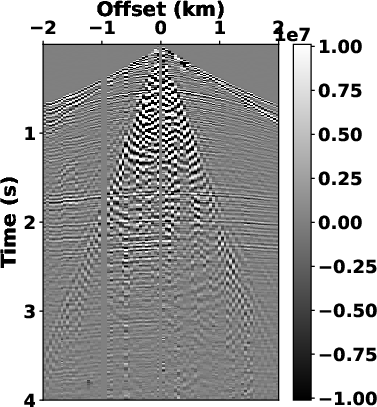
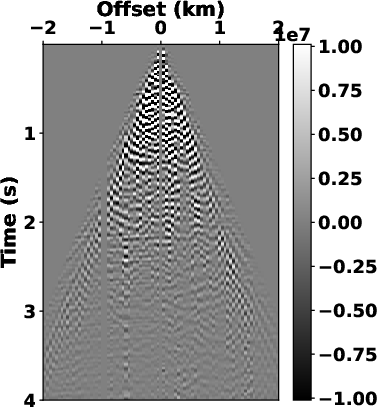
We first use an open-source OZ-25 dataset, which is a typical dataset
suitable for testing the ground-roll noise attenuation performance and
has been widely used in the geophysics
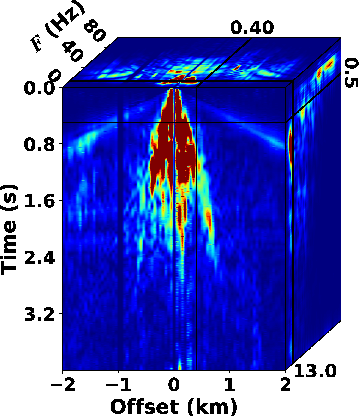
community (Chen et al., 2015; Yilmaz, 1987; Tao et al., 2020; Yarham et al., 2006). Fig.5a
shows the raw dataset in common-shot domain with 81 traces and 2000
samples per trace. The temporal and spatial sampling intervals are
0.002 s and 0.05 km, respectively. We use the proposed SLTFT to
generate the
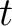 -
-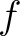 -
-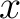 spectrum coefficients (see
Fig.5b). The noise energy is primarily concentrated
within a triangular zone surrounding the near offset in low frequency
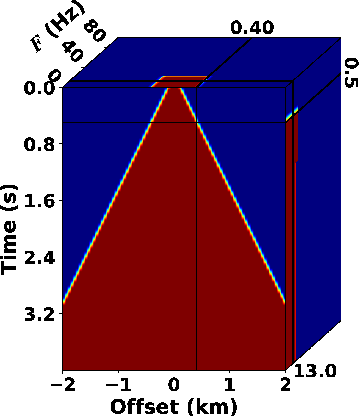
band. We borrow a similar strategy from Liu and Fomel (2013) and design a
filter mask to attenuate the noise energy cluster localized in both
frequency and space (see Fig.5c). Then we use the
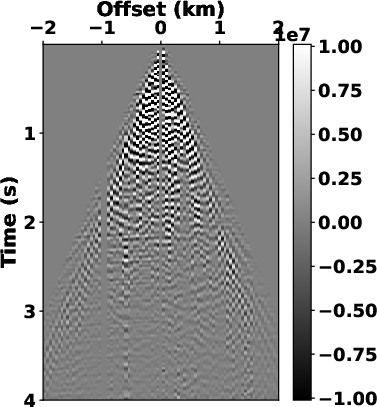
inverse SLTFT to bring back the separated signal (see
Fig.6e). The denoised dataset shows that the strong
interference noise is well-attenuated and the reflection signals are
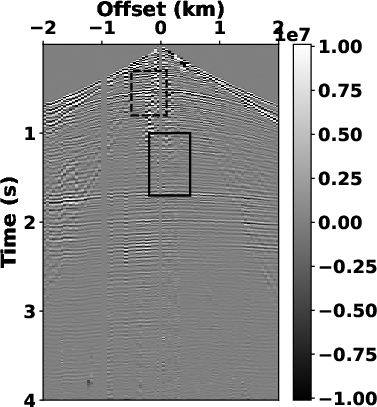
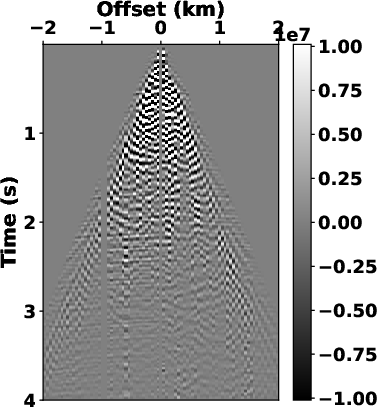
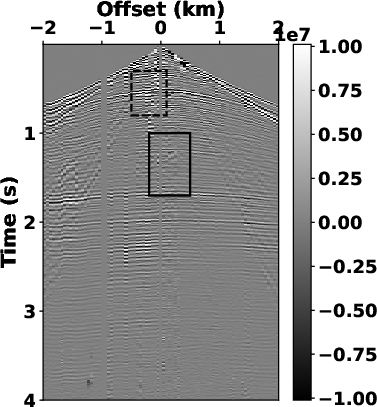
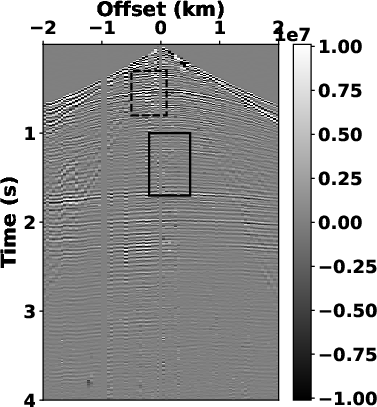
preserved. We use bandpass filtering (see Fig.6a) and LTF
decomposition (see Fig.6c) to compare the denoising
performance.
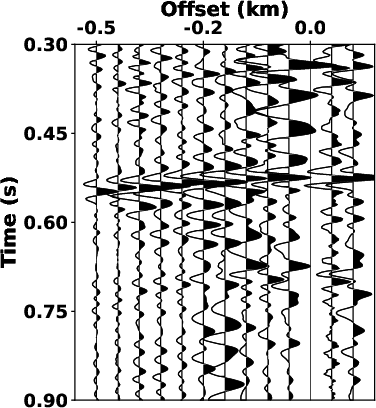
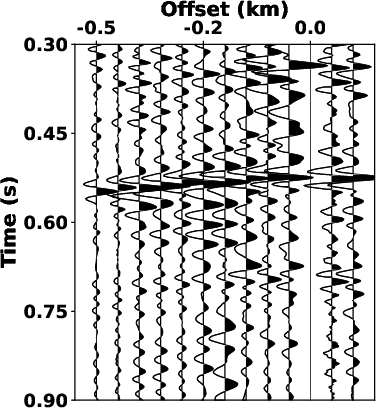
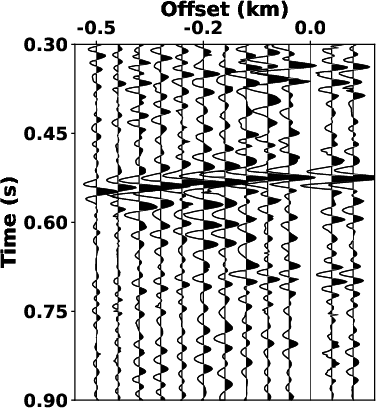
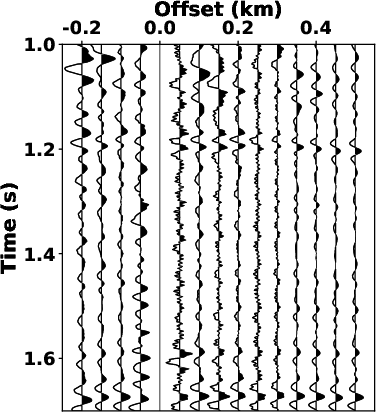
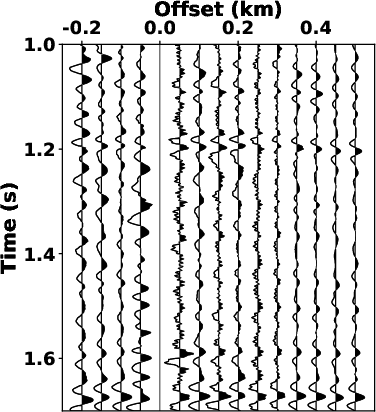
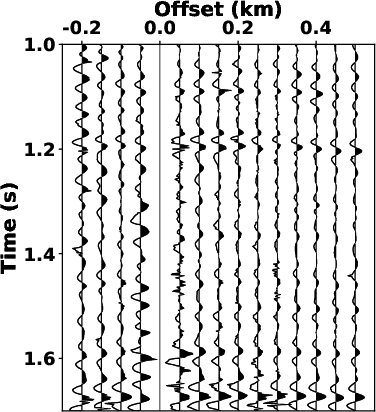
Fig.7
shows zoomed-in sections from the separated signals in
Fig.6.
Fig.7a
and 7d show that the bandpass filtering fails to
attenuate the overlapped noise. Compared to the denoised results of
LTF decomposition in Fig.7b
and 7e, the proposed SLTFT method brought more
satisfactory results (see Fig.7c
and 7f) with the strong interference noise is
well-attenuated.
spectrum coefficients (see
Fig.5b). The noise energy is primarily concentrated
within a triangular zone surrounding the near offset in low frequency
band. We borrow a similar strategy from Liu and Fomel (2013) and design a
filter mask to attenuate the noise energy cluster localized in both
frequency and space (see Fig.5c). Then we use the
inverse SLTFT to bring back the separated signal (see
Fig.6e). The denoised dataset shows that the strong
interference noise is well-attenuated and the reflection signals are
preserved. We use bandpass filtering (see Fig.6a) and LTF
decomposition (see Fig.6c) to compare the denoising
performance.
Fig.7
shows zoomed-in sections from the separated signals in
Fig.6.
Fig.7a
and 7d show that the bandpass filtering fails to
attenuate the overlapped noise. Compared to the denoised results of
LTF decomposition in Fig.7b
and 7e, the proposed SLTFT method brought more
satisfactory results (see Fig.7c
and 7f) with the strong interference noise is
well-attenuated.
|
|---|
|
field,sltft,cmask
Figure 5. (a) Raw OZ-25 dataset, (b) the 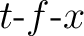 spectrum obtained by the SLTFT
( spectrum obtained by the SLTFT
(
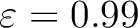 ) and (c) the filter mask in ) and (c) the filter mask in
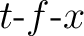 domain. domain.
|
|
|
|
|---|
|
bp,bp_err,iltft,iltft_err,isltft,isltft_err
Figure 6. Estimated signals and separated noise using (a) and (b) high-pass filter with 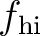 =20 Hz, (c) and (d) LTF decomposition, (e) and (f) the
proposed SLTFT. =20 Hz, (c) and (d) LTF decomposition, (e) and (f) the
proposed SLTFT.
|
|
|
|
|---|
|
bp_wig1,iltft_wig1,isltft_wig1,bp_wig2,iltft_wig2,isltft_wig2
Figure 7. Magnified sections of the denoised profile in Fig.6. (a), (b) and (c) correspond to the sections outlined by dashed rectangles in Figs. 6a, 6c, and 6e, respectively. (d), (e) and (f) correspond to the sections outlined by dashed rectangles in Figs. 6a, 6c, and 6e, respectively. |
|
|
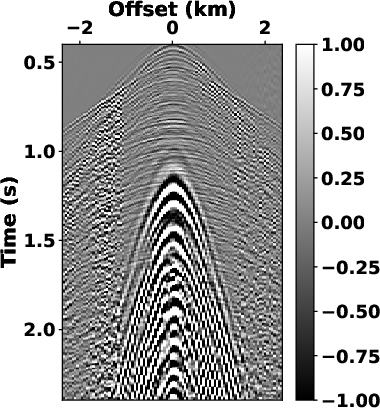
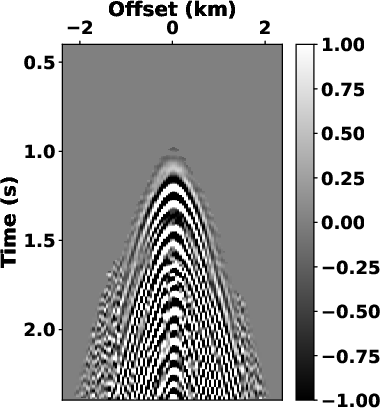
Next, we use another widely-used field dataset, the Saudi Arabia Dune
dataset, to further test the performance of the proposed method. The
field dataset contains strong ground-roll noise with hyperbolic
moveout (see Fig.8a) and is popular as a benchmark
dataset for ground-roll noise
attenuation (Yang et al., 2024; Zheng et al., 2022; Fomel, 2002; Kaur et al., 2020). We use a
mask filter in the
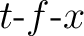 domain (see
Fig.8c) to suppress the ground-roll noise. The
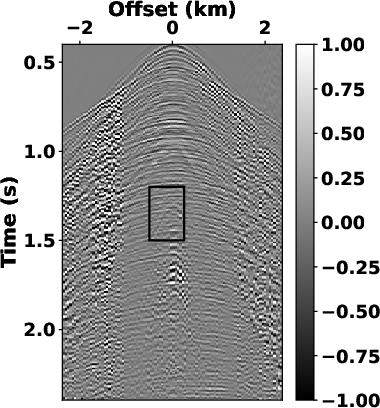
estimated signal by using the high-pass filter with 20-Hz cutoff
frequency contains more low-level ground-roll noise (see
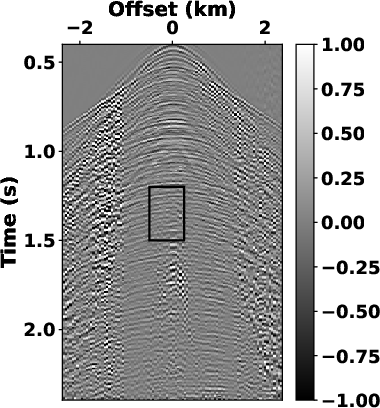
Fig.9a). The denoised dataset obtained by the
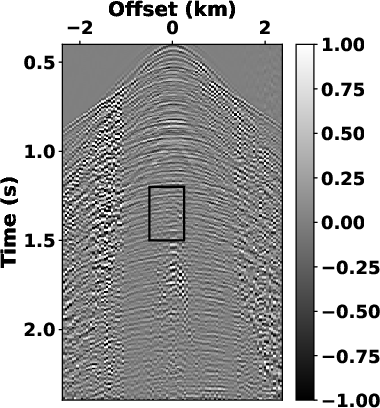
proposed SLTFT (see Fig.8b) shows that the proposed
method achieved the separation goal that the underlying reflection
events clearly appear in the estimated section, and the ground-roll
noise is well suppressed.
domain (see
Fig.8c) to suppress the ground-roll noise. The
estimated signal by using the high-pass filter with 20-Hz cutoff
frequency contains more low-level ground-roll noise (see
Fig.9a). The denoised dataset obtained by the
proposed SLTFT (see Fig.8b) shows that the proposed
method achieved the separation goal that the underlying reflection
events clearly appear in the estimated section, and the ground-roll
noise is well suppressed.
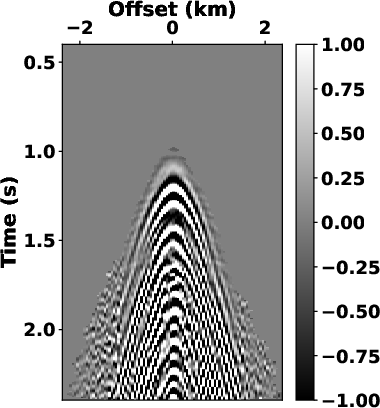
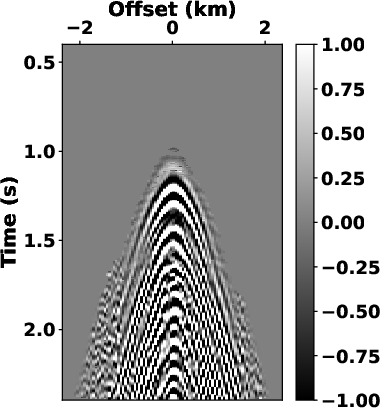
Although the LTF decomposition can also produce a reasonable result (see Fig.6c and 9c), its computational cost is way too much. The proposed method demonstrates a significant reduction in time cost, for example, the computational time by the SLTFT is 7.77 s for the OZ-25 dataset and 1.90 s for the Dune dataset when compared with 62.37 s and 16.69 s needed from the LTF decomposition.
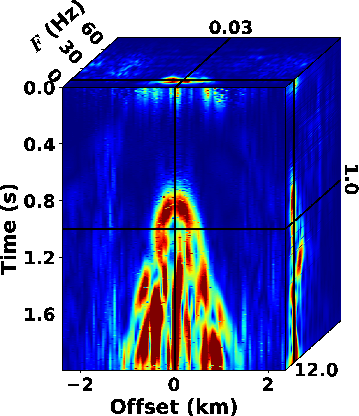
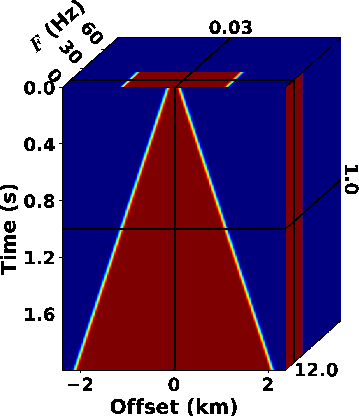
|
|---|
|
dat,sltft,cmask
Figure 8. (a) Raw Saudi Arabia Dune dataset, (b) the 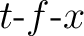 spectrum obtained by
the SLTFT ( spectrum obtained by
the SLTFT (
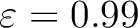 ) and the filter mask in ) and the filter mask in
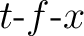 domain. domain.
|
|
|
|
|---|
|
bpsign,bpnoiz,ltftsign,ltftnoiz,sltftsign,sltftnoiz
Figure 9. Estimated signals and separated noise using (a) and (b) high-pass filter with 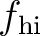 =24 Hz, (c) and (d) LTF decomposition, (e)
and (f) the proposed SLTFT. =24 Hz, (c) and (d) LTF decomposition, (e)
and (f) the proposed SLTFT.
|
|
|