|
|
|
|
Fast Streaming Local Time-frequency Transform for Nonstationary Seismic Data Processing |
Next: Adaptive Time-frequency Localization of Up: Theory Previous: Theory
![$s[n]$](img11.png) with a fixed length
of
with a fixed length
of 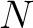 , its Fourier series can be derived by the inner product of the
signal with a family of sines and cosines
where
, its Fourier series can be derived by the inner product of the
signal with a family of sines and cosines
where 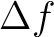 is the frequency interval,
is the frequency interval, 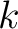 and
and 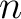 are the
discrete frequency index and time index, respectively.
are the
discrete frequency index and time index, respectively. ![$C[k]$](img17.png) are the
Fourier coefficients,
are the
Fourier coefficients,
![$\psi_k[n] = \exp\left[-\text{j}2\pi k\Delta f
(n/N)\right]$](img18.png) are the complex-value bases, and
are the complex-value bases, and ![$[\cdot]$](img19.png) stands for
the index of a discrete sequence. The signal can be expressed by the
inverse form of equation 1, which is written as
where
stands for
the index of a discrete sequence. The signal can be expressed by the
inverse form of equation 1, which is written as
where
![$\psi^*_k[n]$](img21.png) is the complex conjugate of
is the complex conjugate of ![$\psi_k[n]$](img22.png) . We can
rewrite the equation 2 in a prediction-error regression
form as
. We can
rewrite the equation 2 in a prediction-error regression
form as
![$e[n]$](img24.png) is the prediction error. Then we can apply the
nonstationary regression (Fomel, 2009) to the Fourier series
regression in equation 3, which allows the coefficients
is the prediction error. Then we can apply the
nonstationary regression (Fomel, 2009) to the Fourier series
regression in equation 3, which allows the coefficients
![$C[k]$](img17.png) to vary over time coordinate
to vary over time coordinate 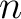 . The error turns
into (Fomel, 2009)
The nonstationary coefficients
. The error turns
into (Fomel, 2009)
The nonstationary coefficients ![$C[k,n]$](img26.png) can be obtained by solving the
least-squares minimization problem(Liu and Fomel, 2013):
can be obtained by solving the
least-squares minimization problem(Liu and Fomel, 2013):
The nonstationary regression makes the minimization of equation 5 become ill-posed, and a reasonable solution is to include additional constraints. Classical regularization methods, such as Tikhonov regularization (Tikhonov, 1963) and shaping regularization (Liu and Fomel, 2013; Chen, 2021; Fomel, 2007b), can be used to solve the ill-posed problem. The streaming computation is an efficient algorithm which enables a fast way to solve the nonstationary regression (Fomel and Claerbout, 2016,2024; Geng et al., 2024). It employs a streaming regularization, where the new coefficients are assumed to be close to the previous ones
In matrix notation, these conditions can be combined into an overdetermined linear system (Fomel and Claerbout, 2016,2024):where
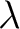 is the parameter that controls the deviation of
is the parameter that controls the deviation of
![$C[k,n]$](img26.png) from
from ![$C[k,n-1]$](img31.png) . To simplify the notation, one can rewrite
equation 7 in a shortened block-matrix form as
. To simplify the notation, one can rewrite
equation 7 in a shortened block-matrix form as
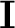 is an identity matrix and
is an identity matrix and
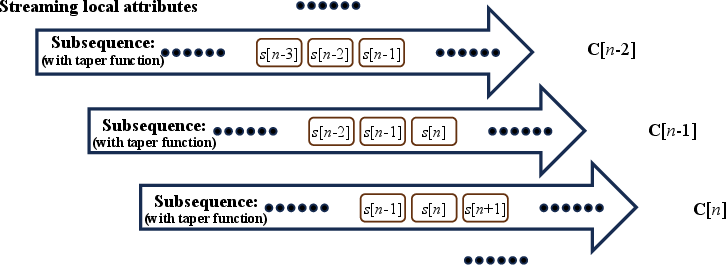
However, the streaming regularization in equation 6
offers an equal approximation for all previous time samples, which
means ![$C[k,0]$](img35.png) influences
influences ![$C[k,n]$](img26.png) as much as
as much as ![$C[k,n-1]$](img31.png) does. This
leads to a global frequency spectrum (similar to the discrete Fourier
transform) rather than a local one. Hence, Geng et al. (2024) uses the
taper strategy and performs streaming computations repeatedly to
obtain the local frequency attributes. Although streaming algorithm
can speed up the progress, it has a limited efficiency due to a large
amount of repetitive calculations caused by the window functions. In
this study, we introduced a localization scalar
does. This
leads to a global frequency spectrum (similar to the discrete Fourier
transform) rather than a local one. Hence, Geng et al. (2024) uses the
taper strategy and performs streaming computations repeatedly to
obtain the local frequency attributes. Although streaming algorithm
can speed up the progress, it has a limited efficiency due to a large
amount of repetitive calculations caused by the window functions. In
this study, we introduced a localization scalar
 to limit
the smoothing radius and avoid the repeated computations brought by
taper functions. The modified inverse problem is expressed as follows
to limit
the smoothing radius and avoid the repeated computations brought by
taper functions. The modified inverse problem is expressed as follows
The localization scalarin
 is defined in
is defined in
![$\left(0,1\right]$](img38.png) and provides a decaying and localized smoothing
constraint that
and provides a decaying and localized smoothing
constraint that
![$\mathbf{C}[n]$](img43.png) can be obtained by
can be obtained by
Equation 15 shows that the coefficients
![$\mathbf{C}[n]$](img43.png) at
at 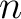 is calculated by the data point
is calculated by the data point ![$s[n]$](img11.png) and the
previous coefficients
and the
previous coefficients
![$\mathbf{C}[n-1]$](img45.png) , but the frequency information
of the data points after
, but the frequency information
of the data points after 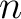 is not included.
is not included.
This could lead to a small time-shift in the time-frequency domain. To
avoid the time-shift effect, we obtain the center-localized spectrum
by implementing the streaming computation forward and backward along
the time direction and adding the results
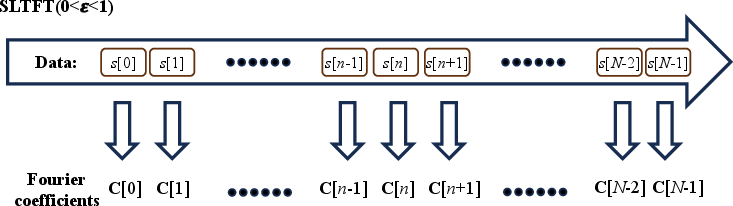
together. Fig.1 illustrates the
main processes of the proposed SLTFT and the streaming local
attribute (Geng et al., 2024). The proposed method avoids repeatedly
windowing the data, and can obtain the result streamingly all at
once. Analogous to LTF decomposition (Liu and Fomel, 2013), the absolute
value of
![$\vert\mathbf{C}[n]\vert$](img46.png) represents the localized time-frequency
distribution of
represents the localized time-frequency
distribution of ![$s[n]$](img11.png) , and equation 15 can be simply
inverted to reconstruct the original data
, and equation 15 can be simply
inverted to reconstruct the original data ![$s[n]$](img11.png) from the coefficients
from the coefficients
![$\mathbf{C}[n]$](img43.png) (Fomel and Claerbout, 2016,2024):
(Fomel and Claerbout, 2016,2024):
The inversion using equation 16 is suffer from the
trade-off between accuracy and
efficiency (Fomel and Claerbout, 2024,2016). Another way to reconstruct the
original data is to directly apply the
equation 2. Additionally, we use an amplitude recovery
factor  defined by
defined by
![$\hat{\mathbf{C}}[n]$](img50.png) can be obtained by
and the original signal
can be obtained by
and the original signal ![$s[n]$](img11.png) can be precisely reconstructed by
can be precisely reconstructed by
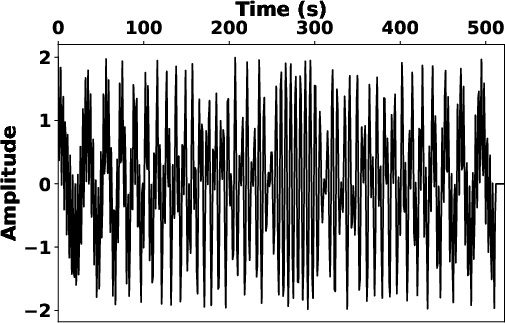
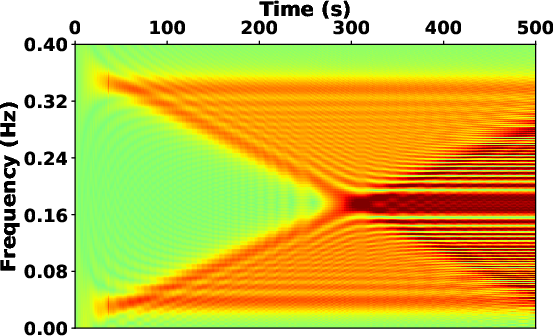
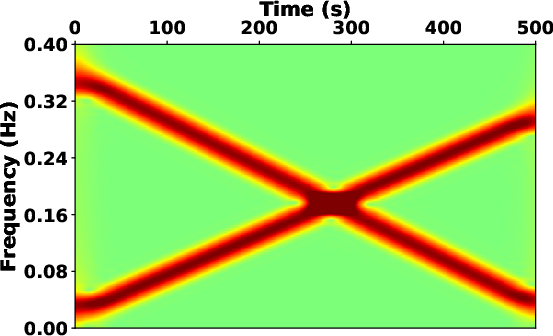
We utilize a benchmark chirp signal (see Fig.2a) to further illustrate the role of the localization scalar. Fig.2b presents the time-frequency map derived from the streaming local attribute (Geng et al., 2024), which fails in providing a localized time-frequency map if the taper function is removed to reduce the computational costs. However, the proposed SLTFT without window functions can provide a reasonable result (see Fig.2c).
Compared to the streaming local attribute with the taper function, the
proposed SLTFT by updating the coefficients according to
equation 15 requires only elementary algebraic
operations, which effectively reduces computational cost without
iteration. According to equation 9,
![$\mathbf{C}[n]$](img43.png) is a
is a
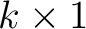 vector and the size of
vector and the size of
![$\mathbf{\Psi}[n]$](img54.png) is
is 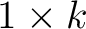 for any
for any 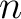 , thus the computational complexities of
, thus the computational complexities of
![$\varepsilon^2\mathbf{\Psi}[n]\mathbf{C}[n-1]\mathbf{\Psi}^T[n]$](img56.png) and
and
![$s[n]\mathbf{\Psi}^T[n]$](img57.png) are both
are both 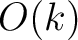 . Meanwhile,
. Meanwhile,
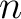 and is computed only once.
According to equations 15 and 18, the
computational complexity of the proposed SLTFT method is
and is computed only once.
According to equations 15 and 18, the
computational complexity of the proposed SLTFT method is
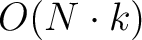 . Table 1 compares the complexities of different
approaches, which shows the proposed method has the lowest requirement
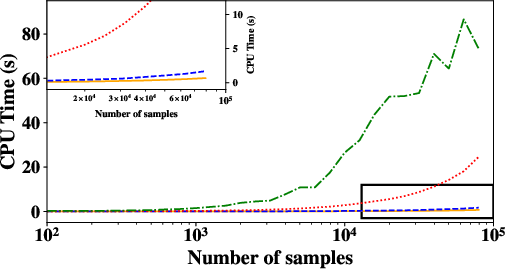
for computational resources. Fig.3 further shows the CPU
time of the different methods. We select the fixed frequency sample of
500 and the fixed window length of 100 (for those who need a taper
function). The number of iteration is set to 50 in the LTF
decomposition. All these records are obtained by taking the average of
5 measurements. Fig.3 is visually in line with the
theoretical complexity shown in table 1. It is clear
that the proposed method offers a fast transform almost equivalent to
the STFT and is much more efficient than the LTF decomposition and the
streaming local attributes method. Moreover, it combines the
advantages of flexible frequency sampling and the adaptability of time
and frequency localization, which are not achievable with the
STFT. This enables fast local time-frequency analysis and processing,
especially for large-scale seismic data, e.g., passive seismic
data (Geng et al., 2024).
. Table 1 compares the complexities of different
approaches, which shows the proposed method has the lowest requirement
for computational resources. Fig.3 further shows the CPU
time of the different methods. We select the fixed frequency sample of
500 and the fixed window length of 100 (for those who need a taper
function). The number of iteration is set to 50 in the LTF
decomposition. All these records are obtained by taking the average of
5 measurements. Fig.3 is visually in line with the
theoretical complexity shown in table 1. It is clear
that the proposed method offers a fast transform almost equivalent to
the STFT and is much more efficient than the LTF decomposition and the
streaming local attributes method. Moreover, it combines the
advantages of flexible frequency sampling and the adaptability of time
and frequency localization, which are not achievable with the
STFT. This enables fast local time-frequency analysis and processing,
especially for large-scale seismic data, e.g., passive seismic
data (Geng et al., 2024).
|
|---|
|
streamingLTFTa,streamingLTFTb
Figure 1. Schematic illustration of (a) the proposed SLTFT and (b) the streaming local attributes method. |
|
|
|
|---|
|
cchirps,sltft,sltft1
Figure 2. Schematic illustration of (a) the synthetic chirp signal and its time-frequency map obtained by (b) the streaming local attributes without window and (c) the proposed SLTFT. |
|
|
|
|---|
|
time
Figure 3. The CPU time comparison among the time-frequency analysis methods. Orange line: STFT; blue dash line: SLTFT; red dot line: streaming attributes; green dash-dot line: LTF decomposition. The convergence speed affects the CPU time of the LTF decomposition, resulting in a non-smooth curve. |
|
|