|
|
|
|
Dip and offset together |
|
Cos1
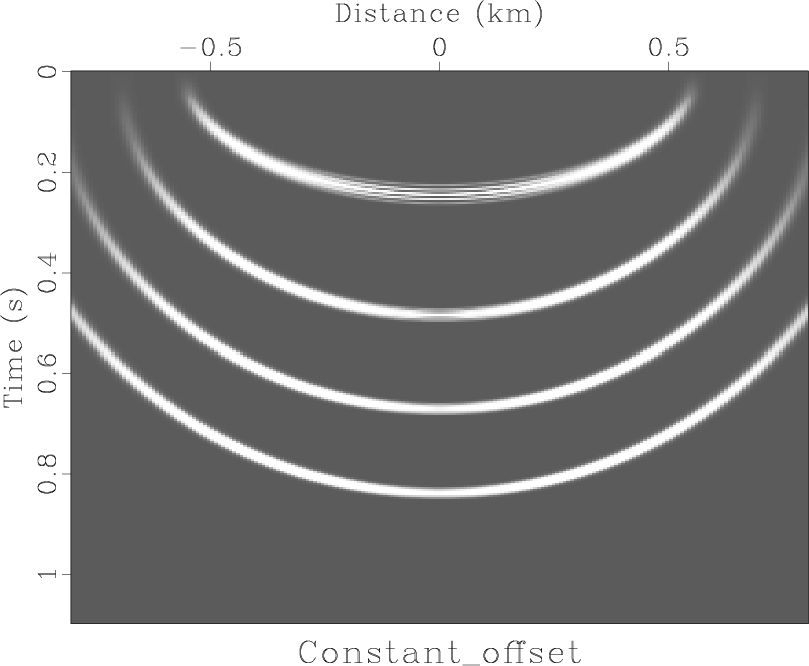
Figure 4. Migrating impulses on a constant-offset section. Notice that shallow impulses (shallow compared to |
|
|---|---|
|
|
|
Cos0
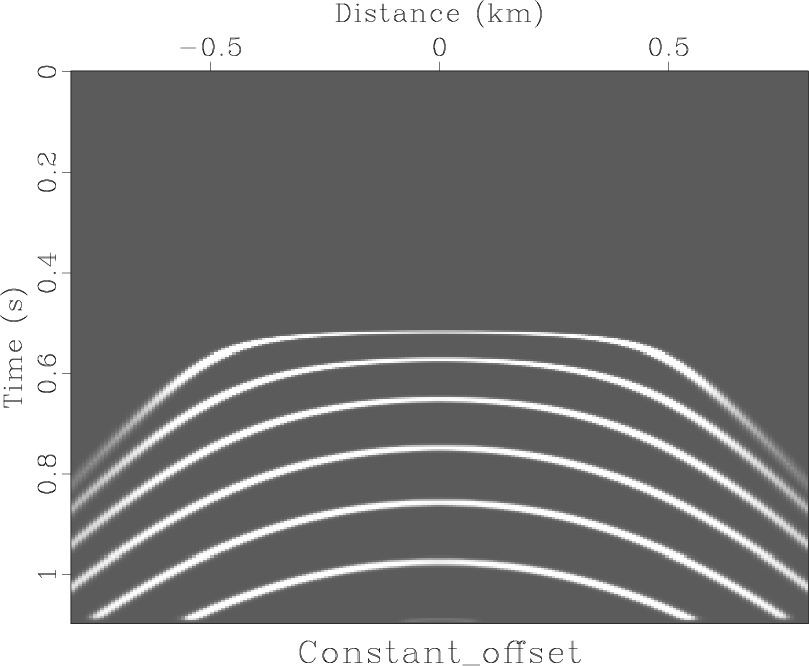
Figure 5. Forward modeling from an earth impulse. |
|
|---|---|
|
|
It is not easy to show that equation (8.5) can be
cast in the standard mathematical form of an ellipse, namely,
a stretched circle.
But the result is a simple one,
and an important one for later analysis.
Feel free to skip forward over the following verification
of this ancient wisdom.
To help reduce algebraic verbosity,
define a new ![]() equal to the old one shifted by
equal to the old one shifted by ![]() .
Also make the definitions
.
Also make the definitions
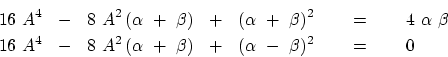
| (10) | |||
| (11) |
Fixing ![]() , equation (8.9) is the equation for a circle with
a stretched
, equation (8.9) is the equation for a circle with
a stretched ![]() -axis.
The above algebra confirms that the
``string and tack'' definition of an ellipse
matches the ``stretched circle'' definition.
An ellipse in earth model space corresponds
to an impulse on a constant-offset section.
-axis.
The above algebra confirms that the
``string and tack'' definition of an ellipse
matches the ``stretched circle'' definition.
An ellipse in earth model space corresponds
to an impulse on a constant-offset section.
|
|
|
|
Dip and offset together |