Prestack migration ellipse

Next: Constant offset migration Up: PRESTACK MIGRATION Previous: Cheops' pyramid

Prestack migration ellipse

Denoting the horizontal coordinate

of the scattering point by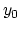

Equation (8.1) in

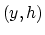-space is

$\begin{displaymath} t v \eq \sqrt { z^2 + {( y - y_0 - h) }^2} + \sqrt { z^2 + {( y - y_0 + h) }^2} \end{displaymath}$

(5)

A basic insight into equation (8.1) is to notice that at constant-offset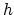

and constant travel time

the locus of possible reflectors is an ellipse in the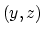

-plane centered at

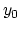. The reason it is an ellipse follows from the geometric definition of an ellipse. To draw an ellipse, place a nail or tack into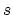

on Figure 8.1 and another into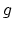

. Connect the tacks by a string that is exactly long enough to go through

. An ellipse going through

may be constructed by sliding a pencil along the string, keeping the string tight. The string keeps the total distance

constant as is shown in Figure 8.3

ellipse1 Figure 3. Prestack migration ellipse, the locus of all scatterers with constant traveltime for source S and receiver G.

Replacing depth 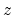in equation (8.5) by the vertical traveltime depth $\tau = 2z/v=z/v_{\rm half}$ we get

$\begin{displaymath} t \eq {1 \over 2}\ \left( \sqrt { \tau^2 + [( y-y_0)-h]^... ...t { \tau^2 + [( y-y_0)+h]^2 / v_{\rm half}^2 } \ \right) \end{displaymath}$

(6)

Next: Constant offset migration Up: PRESTACK MIGRATION Previous: Cheops' pyramid

2009-03-16