Guide to madagascar programs
This guide introduces some of the most used madagascar programs and illustrates their usage with examples.
Main programs
The source files for these programs can be found under system/main in the Madagascar distribution. The "main" programs perform general-purpose operations on RSF hypercubes regardless of the data dimensionality or physical dimensions.
sfadd
| Add, multiply, or divide RSF datasets. | |||
|---|---|---|---|
| sfadd > out.rsf scale= add= sqrt= abs= log= exp= mode= [< file0.rsf] file1.rsf file2.rsf ... | |||
| The various operations, if selected, occur in the following order: (1) Take absolute value, abs= (2) Add a scalar, add= (3) Take the natural logarithm, log= (4) Take the square root, sqrt= (5) Multiply by a scalar, scale= (6) Compute the base-e exponential, exp= (7) Add, multiply, or divide the data sets, mode= sfadd operates on integer, float, or complex data, but all the input and output files must be of the same data type. An alternative to sfadd is sfmath, which is more versatile, but may be less efficient. | |||
| bools | abs= | If true take absolute value [nin] | |
| floats | add= | Scalar values to add to each dataset [nin] | |
| bools | exp= | If true compute exponential [nin] | |
| bools | log= | If true take logarithm [nin] | |
| string | mode= | 'a' means add (default), 'p' or 'm' means multiply, 'd' means divide | |
| floats | scale= | Scalar values to multiply each dataset with [nin] | |
| bools | sqrt= | If true take square root [nin] | |
sfadd is useful for combining (adding, dividing, or multiplying) several datasets. What if you want to subtract two datasets? Easy. Use the scale parameter as follows:
bash$ sfadd data1.rsf data2.rsf scale=1,-1 > diff.rsf
or
bash$ sfadd < data1.rsf data2.rsf scale=1,-1 > diff.rsf
The same task can be accomplished with the more general sfmath program:
bash$ sfmath one=data1.rsf two=data2.rsf output='one-two' > diff.rsf
or
bash$ sfmath < data1.rsf two=data2.rsf output='input-two' > diff.rsf
In both cases, the size and shape of data1.rsf and data2.rsf hypercubes should be the same, and a warning message is printed out if the the axis sampling parameters (such as o1 or d1) in these files are different.
Implementation: system/main/add.c
The first input file is either in the list or in the standard input.
/* find number of input files */
if (isatty(fileno(stdin))) {
/* no input file in stdin */
nin=0;
} else {
in[0] = sf_input("in");
nin=1;
}Collect input files in the in array from all command-line parameters that don't contain an "=" sign. The total number of input files in nin.
for (i=1; i< argc; i++) { /* collect inputs */
if (NULL != strchr(argv[i],'=')) continue;
in[nin] = sf_input(argv[i]);
nin++;
}
if (0==nin) sf_error ("no input");
/* nin = no of input files*/A helper function check_compat checks the compatibility of input files.
static void
check_compat (sf_datatype type /* data type */,
size_t nin /* number of files */,
sf_file* in /* input files [nin] */,
int dim /* file dimensionality */,
const int* n /* dimensions [dim] */)
/* Check that the input files are compatible.
Issue error for type mismatch or size mismatch.
Issue warning for grid parameters mismatch. */
{
int ni, id;
size_t i;
float d, di, o, oi;
char key[3];
const float tol=1.e-5; /* tolerance for comparison */
for (i=1; i < nin; i++) {
if (sf_gettype(in[i]) != type)
sf_error ("type mismatch: need %d",type);
for (id=1; id <= dim; id++) {
(void) snprintf(key,3,"n%d",id);
if (!sf_histint(in[i],key,&ni) || ni != n[id-1])
sf_error("%s mismatch: need %d",key,n[id-1]);
(void) snprintf(key,3,"d%d",id);
if (sf_histfloat(in[0],key,&d)) {
if (!sf_histfloat(in[i],key,&di) ||
(fabsf(di-d) > tol*fabsf(d)))
sf_warning("%s mismatch: need %g",key,d);
} else {
d = 1.;
}
(void) snprintf(key,3,"o%d",id);
if (sf_histfloat(in[0],key,&o) &&
(!sf_histfloat(in[i],key,&oi) ||
(fabsf(oi-o) > tol*fabsf(d))))
sf_warning("%s mismatch: need %g",key,o);
}
}
}Finally, we enter the main loop, where input data are getting read buffer by buffer and combined in the total product depending on the data type.
for (nbuf /= sf_esize(in[0]); nsiz > 0; nsiz -= nbuf) {
if (nbuf > nsiz) nbuf=nsiz;
for (j=0; j < nin; j++) {
collect = (bool) (j != 0);
switch(type) {
case SF_FLOAT:
sf_floatread((float*) bufi,
nbuf,
in[j]);
add_float(collect,
nbuf,
(float*) buf,
(const float*) bufi,
cmode,
scale[j],
add[j],
abs_flag[j],
log_flag[j],
sqrt_flag[j],
exp_flag[j]);
break;The data combination program for floating point numbers is add_float.
static void add_float (bool collect, /* if collect */
size_t nbuf, /* buffer size */
float* buf, /* output [nbuf] */
const float* bufi, /* input [nbuf] */
char cmode, /* operation */
float scale, /* scale factor */
float add, /* add factor */
bool abs_flag, /* if abs */
bool log_flag, /* if log */
bool sqrt_flag, /* if sqrt */
bool exp_flag /* if exp */)
/* Add floating point numbers */
{
size_t j;
float f;
for (j=0; j < nbuf; j++) {
f = bufi[j];
if (abs_flag) f = fabsf(f);
f += add;
if (log_flag) f = logf(f);
if (sqrt_flag) f = sqrtf(f);
if (1. != scale) f *= scale;
if (exp_flag) f = expf(f);
if (collect) {
switch (cmode) {
case 'p': /* product */
case 'm': /* multiply */
buf[j] *= f;
break;
case 'd': /* delete */
if (f != 0.) buf[j] /= f;
break;
default: /* add */
buf[j] += f;
break;
}
} else {
buf[j] = f;
}
}
}sfattr
| Display dataset attributes. | |||
|---|---|---|---|
| sfattr < in.rsf want= | |||
Sample output from "sfspike n1=100 | sfbandpass fhi=60 | sfattr" ******************************************* rms = 0.992354 mean value = 0.987576 2-norm value = 9.92354 variance = 0.00955481 standard deviation = 0.0977487 maximum value = 1.12735 at 97 minimum value = 0.151392 at 100 number of nonzero samples = 100 total number of samples = 100 ******************************************* rms = sqrt[ sum(data^2) / n ] mean = sum(data) / n norm = sum(abs(data)^lval)^(1/lval) variance = [ sum(data^2) - n*mean^2 ] / [ n-1 ] standard deviation = sqrt [ variance ] | |||
| int | lval=2 | norm option, lval is a non-negative integer, computes the vector lval-norm | |
| string | want= | 'all'(default),'rms','mean','norm','var','std','max','min','nonzero','samples','short'
| |
sfattr is a useful diagnostic program. It reports certain
statistical values for an RSF dataset: RMS (root-mean-square)
amplitude, mean value, vector norm value, variance, standard deviation,
maximum and minimum values, number of nonzero samples, and the total
number of samples.
If we denote data values as for , then the RMS
value is , the mean
value is , the -norm value
is , the variance is
, and the standard
deviation is the square root of the variance. Using sfattr
is a quick way to see the distribution of data values and check it for anomalies.
The output can be parsed using utilities such as awk, to extract only a numeric value for feeding it as a parameter value into a command line interface. Notice the backticks in the example below: <bash> sfgrey <vel.rsf allpos=y bias=`sfattr <vel.rsf want=min | awk '{print $4}'` | sfpen </bash>
Implementation: system/main/attr.c
Computations start by finding the input data (in) size (nsiz) and dimensions (dim).
dim = (size_t) sf_filedims (in,n);
for (nsiz=1, i=0; i < dim; i++) {
nsiz *= n[i];
}
In the main loop, we read the input data buffer by buffer.
for (nleft=nsiz; nleft > 0; nleft -= nbuf) {
nbuf = (bufsiz < nleft)? bufsiz: nleft;
switch (type) {
case SF_FLOAT:
sf_floatread((float*) buf,nbuf,in);
break;
case SF_INT:
sf_intread((int*) buf,nbuf,in);
break;
case SF_COMPLEX:
sf_complexread((sf_complex*) buf,nbuf,in);
break;
case SF_UCHAR:
sf_ucharread((unsigned char*) buf,nbuf,in);
break;
case SF_CHAR:
default:
sf_charread(buf,nbuf,in);
break;
}
The data attributes are accumulated in corresponding double-precision
variables.
fsum += f;
fsqr += f*f;
Finally, the attributes are reduced and printed out.
fmean = fsum/nsiz;
if (lval==2) fnorm = sqrt(fsqr);
else if (lval==0) fnorm = nsiz-nzero;
else fnorm = pow(flval,1./lval);
frms = sqrt(fsqr/nsiz);
if (nsiz > 1) fvar = (fsqr-nsiz*fmean*fmean)/(nsiz-1);
else fvar = 0.0;
fstd = sqrt(fvar); if(NULL==want || 0==strcmp(want,"rms"))
printf("rms = %g \n",(float) frms);
if(NULL==want || 0==strcmp(want,"mean"))
printf("mean value = %g \n",(float) fmean);
if(NULL==want || 0==strcmp(want,"norm"))
printf("%d-norm value = %g \n",lval,(float) fnorm);
if(NULL==want || 0==strcmp(want,"var"))
printf("variance = %g \n",(float) fvar);
if(NULL==want || 0==strcmp(want,"std"))
printf("standard deviation = %g \n",(float) fstd);sfcat
| Concatenate datasets. | |||
|---|---|---|---|
| sfcat > out.rsf space= axis=3 nspace=(int) (ni/(20*nin) + 1) [<file0.rsf] file1.rsf file2.rsf ... | |||
| sfmerge inserts additional space between merged data. | |||
| int | axis=3 | Axis being merged | |
| int | nspace=(int) (ni/(20*nin) + 1) | if space=y, number of traces to insert | |
| bool | space= | [y/n] | Insert additional space.
|
sfcat and sfmerge concatenate two or more files
together along a particular axis. It is the same program, only
sfcat has the default space=n and sfmerge
has the default space=y.
Example of sfcat:
bash$ sfspike n1=2 n2=3 > one.rsf
bash$ sfin one.rsf
one.rsf:
in="/tmp/one.rsf@"
esize=4 type=float form=native
n1=2 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
6 elements 24 bytes
bash$ sfcat one.rsf one.rsf axis=1 > two.rsf
bash$ sfin two.rsf
two.rsf:
in="/tmp/two.rsf@"
esize=4 type=float form=native
n1=4 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
12 elements 48 bytes
Example of sfmerge:
bash$ sfmerge one.rsf one.rsf axis=2 > two.rsf
bash$ sfin two.rsf
two.rsf:
in="/tmp/two.rsf@"
esize=4 type=float form=native
n1=2 d1=0.004 o1=0 label1="Time" unit1="s"
n2=7 d2=0.1 o2=0 label2="Distance" unit2="km"
14 elements 56 bytes
In this case, an extra empty trace is inserted between the two merged files. The axes that are not being merged are checked for consistency:
bash$ sfcat one.rsf two.rsf > three.rsf sfcat: n2 mismatch: need 3
Implementation: system/main/cat.c
The first input file is either in the list or in the standard input. <c>
in = (sf_file*) sf_alloc ((size_t) argc,sizeof(sf_file));
if (!sf_stdin()) { /* no input file in stdin */
nin=0;
} else {
in[0] = sf_input("in"); nin=1;
}
</c>
Everything on the command line that does not contain a "=" sign is treated as a file name, and the corresponding file object is added to the list. <c>
for (i=1; i< argc; i++) { /* collect inputs */
if (NULL != strchr(argv[i],'=')) continue; /* not a file */ in[nin] = sf_input(argv[i]); nin++;
}
if (0==nin) sf_error ("no input");
</c>
As explained above, if the space= parameter is not set, it is inferred from the program name: sfmerge corresponds to space=y and sfcat corresponds to space=n. <c>
if (!sf_getbool("space",&space)) {
/* Insert additional space. y is default for sfmerge, n is default for sfcat */ prog = sf_getprog(); if (NULL != strstr (prog, "merge")) { space = true; } else if (NULL != strstr (prog, "cat")) { space = false; } else { sf_warning("%s is neither merge nor cat," " assume merge",prog); space = true; }
}
</c>
Find the axis for the merging (from the command line axis= argument) and figure out two sizes: n1 for everything after the axis and n2 for everything before the axis. <c>
n1=1;
n2=1;
for (i=1; i <= dim; i++) {
if (i < axis) n1 *= n[i-1]; else if (i > axis) n2 *= n[i-1];
}
</c>
In the output, the selected axis will get extended. <c>
/* figure out the length of extended axis */
ni = 0;
for (j=0; j < nin; j++) {
ni += naxis[j];
}
if (space) {
if (!sf_getint("nspace",&nspace)) nspace = (int) (ni/(20*nin) + 1); /* if space=y, number of traces to insert */ ni += nspace*(nin-1);
}
(void) snprintf(key,3,"n%d",axis); sf_putint(out,key,(int) ni);
</c>
The rest is simple: loop through the datasets reading and writing the data in buffer-size chunks and adding extra empty chunks if space=y. <c>
for (i2=0; i2 < n2; i2++) {
for (j=0; j < nin; j++) { for (ni = n1*naxis[j]*esize; ni > 0; ni -= nbuf) { nbuf = (BUFSIZ < ni)? BUFSIZ: ni; sf_charread (buf,nbuf,in[j]); sf_charwrite (buf,nbuf,out); } if (!space || j == nin-1) continue; /* Add spaces */ memset(buf,0,BUFSIZ); for (ni = n1*nspace*esize; ni > 0; ni -= nbuf) { nbuf = (BUFSIZ < ni)? BUFSIZ: ni; sf_charwrite (buf,nbuf,out); } }
}
</c>
sfcdottest
| Generic dot-product test for complex linear operators with adjoints | |||
|---|---|---|---|
| sfcdottest mod=mod.rsf dat=dat.rsf > pip.rsf | |||
| file | dat= | auxiliary input file name | |
| file | mod= | auxiliary input file name | |
A simple demonstration of the program can be made taking advantage that the complex-to-complex FFT is a linear operator:
<bash> sfspike n1=100 | sfrtoc > spike.rsf < spike.rsf sffft axis=1 pad=1 > spike2.rsf sfcdottest sffft mod=spike.rsf dat=spike2.rsf axis=1 pad=1 </bash>
The output should show values identical down to the last decimal:
sfcdottest: L[m]*d=(3.73955,-1.86955) sfcdottest: L'[d]*m=(3.73955,-1.86955)
sfcmplx
| Create a complex dataset from its real and imaginary parts. | |||
|---|---|---|---|
| sfcmplx > cmplx.rsf real.rsf imag.rsf | |||
| There has to be only two input files specified and no additional parameters. |
sfcmplx simply creates a complex dataset from its real and
imaginary parts. The reverse operation can be accomplished with
sfreal and sfimag.
Example of sfcmplx:
bash$ sfspike n1=2 n2=3 > one.rsf
bash$ sfin one.rsf
one.rsf:
in="/tmp/one.rsf@"
esize=4 type=float form=native
n1=2 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
6 elements 24 bytes
bash$ sfcmplx one.rsf one.rsf > cmplx.rsf
bash$ sfin cmplx.rsf
cmplx.rsf:
in="/tmp/cmplx.rsf@"
esize=8 type=complex form=native
n1=2 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
6 elements 48 bytes
Implementation: system/main/cmplx.c
The program flow is simple. First, get the names of the input files. <c>
/* the first two non-parameters are real and imaginary files */
for (i=1; i< argc; i++) {
if (NULL == strchr(argv[i],'=')) { if (NULL == real) { real = sf_input (argv[i]); } else { imag = sf_input (argv[i]); break; } }
}
if (NULL == imag) {
if (NULL == real) sf_error ("not enough input"); /* if only one input, real is in stdin */ imag = real; real = sf_input("in");
}
</c>
The main part of the program reads the real and imaginary parts buffer by buffer and assembles and writes out the complex input. <c>
for (nleft= (size_t) (rsize*resize); nleft > 0; nleft -= nbuf) {
nbuf = (BUFSIZ < nleft)? BUFSIZ: nleft; sf_charread(rbuf,nbuf,real); sf_charread(ibuf,nbuf,imag); for (i=0; i < nbuf; i += resize) { memcpy(cbuf+2*i, rbuf+i,(size_t) resize); memcpy(cbuf+2*i+resize,ibuf+i,(size_t) resize); } sf_charwrite(cbuf,2*nbuf,cmplx);
}
</c>
sfconjgrad
| Generic conjugate-gradient solver for linear inversion | |||
|---|---|---|---|
| sfconjgrad < dat.rsf mod=mod.rsf > to.rsf < from.rsf > out.rsf niter=1 | |||
| int | niter=1 | number of iterations | |
sfconjgrad is a generic program for least-squares linear inversion with the conjugate-gradient method. Suppose you have an executable program <prog> that takes an RSF file from the standard input and produces an RSF file in the standard output. It may take any number of additional parameters but one of them must be adj= that sets the forward (adj=0) or adjoint (adj=1) operations. The program <prog> is typically an RSF program but it could be anything (a script, a multiprocessor MPI program, etc.) as long as it implements a linear operator and its adjoint. There are no restrictions on the data size or shape. You can easily test the adjointness with sfdottest. The sfconjgrad program searches for a vector that minimizes the least-square misfit for the given input data vector .
The pseudocode for sfconjgrad is given at the end of the "Model fitting with least squares" chapter of Imaging Estimation by Example by Jon Claerbout, with the earliest form published in "Conjugate Gradient Tutorial" (SEP-48, 1986, same author). A simple toy implementation with a small matrix shows that this is algorithm produces the same steps as the algorithm described in equations 45-49 of "An introduction to the Conjugate Gradient Method Without the Agonizing Pain" by J.R. Shewchuk, 1994, when the equation (in Shewchuk's notation) is solved. Multiplying with the transpose ensures a correct solution even when matrix A is square but not symmetric, or not square at all. The program sfcconjgrad implements this algorithm for the case when inputs are complex.
Here is an example. The sfhelicon program implements Claerbout's multidimensional helical filtering (Claerbout, 1998[1]). It requires a filter to be specified in addition to the input and output vectors. We create a helical 2-D filter using the Unix echo command.
bash$ echo 1 19 20 n1=3 n=20,20 data_format=ascii_int in=lag.rsf > lag.rsf bash$ echo 1 1 1 a0=-3 n1=3 data_format=ascii_float in=flt.rsf > flt.rsf
Next, we create an example 2-D model and data vector with sfspike.
bash$ sfspike n1=50 n2=50 > vec.rsf
The sfdottest program can perform the dot product test to check that the adjoint mode works correctly.
bash$ sfdottest sfhelicon filt=flt.rsf lag=lag.rsf mod=vec.rsf dat=vec.rsf sfdottest: L[m]*d=5.28394 sfdottest: L'[d]*m=5.28394
Your numbers may be different because sfdottest generates new random input on each run. Next, let us make some random data with sfnoise.
bash$ sfnoise seed=2005 rep=y < vec.rsf > dat.rsf
and try to invert the filtering operation using sfconjgrad:
bash$ sfconjgrad sfhelicon filt=flt.rsf lag=lag.rsf mod=vec.rsf < dat.rsf > mod.rsf niter=10 sfconjgrad: iter 1 of 10 sfconjgrad: grad=3253.65 sfconjgrad: iter 2 of 10 sfconjgrad: grad=289.421 sfconjgrad: iter 3 of 10 sfconjgrad: grad=92.3481 sfconjgrad: iter 4 of 10 sfconjgrad: grad=36.9417 sfconjgrad: iter 5 of 10 sfconjgrad: grad=18.7228 sfconjgrad: iter 6 of 10 sfconjgrad: grad=11.1794 sfconjgrad: iter 7 of 10 sfconjgrad: grad=7.26941 sfconjgrad: iter 8 of 10 sfconjgrad: grad=5.15945 sfconjgrad: iter 9 of 10 sfconjgrad: grad=4.23055 sfconjgrad: iter 10 of 10 sfconjgrad: grad=3.57495
The output shows that, in 10 iterations, the norm of the gradient vector decreases by almost 1000. We can check the residual misfit before
bash$ < dat.rsf sfattr want=norm norm value = 49.7801
and after
bash$ sfhelicon filt=flt.rsf lag=lag.rsf < mod.rsf | sfadd scale=1,-1 dat.rsf | sfattr want=norm norm value = 5.73563
In 10 iterations, the misfit decreased by an order of magnitude. The result can be improved by running the program for more iterations.
An equivalent implementation for complex-valued inputs is sfcconjgrad. A simple, lightweight Python implementation can be found in $PYTHONPATH/rsf/conjgrad.py.
sfcp
| Copy or move a dataset. | |||
|---|---|---|---|
| sfcp in.rsf out.rsf | |||
| sfcp - copy, sfmv - move. Mimics standard Unix commands. |
The sfcp and sfmv command imitate the Unix
cp and mv commands and serve for copying and moving
RSF files. Example:
bash$ sfspike n1=2 n2=3 > one.rsf
bash$ sfin one.rsf
one.rsf:
in="/tmp/one.rsf@"
esize=4 type=float form=native
n1=2 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
6 elements 24 bytes
bash$ sfcp one.rsf two.rsf
bash$ sfin two.rsf
two.rsf:
in="/tmp/two.rsf@"
esize=4 type=float form=native
n1=2 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
6 elements 24 bytes
Implementation: system/main/cp.c
First, we look for the two first command-line arguments that don't have the "=" character in them and consider them as the names of the input and the output files. <c>
/* the first two non-parameters are in and out files */
for (i=1; i< argc; i++) {
if (NULL == strchr(argv[i],'=')) { if (NULL == in) { infile = argv[i]; in = sf_input (infile); } else { out = sf_output (argv[i]); break; } }
} if (NULL == in || NULL == out)
sf_error ("not enough input"); </c>
Next, we use library functions sf_cp and sf_rm to do the actual work. <c>
sf_cp(in,out); if (NULL != strstr (sf_getprog(),"mv"))
sf_rm(infile,false,false,false); </c>
sfcut
| Zero a portion of the dataset. | |||
|---|---|---|---|
| sfcut < in.rsf > out.rsf verb=n [j1=1 j2=1 ... f1=0 f2=0 ... n1=n1 n2=n2 ... max1= max2= ... min1= min2= ...] | |||
| jN defines the jump in N-th dimension fN is the window start nN is the window size minN and maxN is the maximum and minimum in N-th dimension Reverse of window. | |||
| bool | verb=n | [y/n] | Verbosity flag |
The sfcut command is related to sfwindow and has the same
set of arguments only instead of extracting the selected window, it fills it
with zeroes. The size of the input data is preserved.
Examples:
bash$ sfspike n1=5 n2=5 > in.rsf bash$ < in.rsf sfdisfil 0: 1 1 1 1 1 5: 1 1 1 1 1 10: 1 1 1 1 1 15: 1 1 1 1 1 20: 1 1 1 1 1 bash$ < in.rsf sfcut n1=2 f1=1 n2=3 f2=2 | sfdisfil 0: 1 1 1 1 1 5: 1 1 1 1 1 10: 1 0 0 1 1 15: 1 0 0 1 1 20: 1 0 0 1 1 bash$ < in.rsf sfcut j1=2 | sfdisfil 0: 0 1 0 1 0 5: 0 1 0 1 0 10: 0 1 0 1 0 15: 0 1 0 1 0 20: 0 1 0 1 0
sfdd
| Convert between different formats. | |||
|---|---|---|---|
| sfdd < in.rsf > out.rsf line=8 form= type= format= | |||
| string | form= | ascii, native, xdr | |
| string | format= | Element format (for conversion to ASCII) | |
| int | line=8 | Number of numbers per line (for conversion to ASCII) | |
| string | type= | int, float, complex | |
The sfdd program is used to change either the form (ascii,
xdr, native) or the type (complex, float,
int, char) of the input dataset.
In the example below, we create a plain text (ASCII) file with numbers and
then use sfdd to generate an RSF file in xdr form with
complex numbers.
bash$ cat test.txt
1 2 3 4 5 6
bash$ echo n1=6 data_format=ascii_int in=test.txt > test.rsf
bash$ sfin test.rsf
test.rsf:
in="test.txt"
esize=0 type=int form=ascii
n1=6 d1=? o1=?
6 elements
bash$ sfdd < test.rsf form=xdr type=complex > test2.rsf
bash$ sfin test2.rsf
test2.rsf:
in="/tmp/test2.rsf@"
esize=8 type=complex form=xdr
n1=3 d1=? o1=?
3 elements 24 bytes
bash$ sfdisfil < test2.rsf
0: 1, 2i 3, 4i 5, 6i
To learn more about the RSF data format, consult the guide to RSF format.
sfdisfil
| Print out data values. | |||
|---|---|---|---|
| sfdisfil < in.rsf number=y col=0 format= header= trailer= | |||
Alternatively, use sfdd and convert to ASCII form. | |||
| int | col=0 | Number of columns.
| |
| string | format= | Format for numbers (printf-style).
| |
| string | header= | Optional header string to output before data | |
| bool | number=y | [y/n] | If number the elements |
| string | trailer= | Optional trailer string to output after data | |
The sfdisfil program simply dumps the data contents to the standard
output in a text form. It is used mostly for debugging purposes to quickly
examine RSF files. Here is an example:
bash$ sfmath o1=0 d1=2 n1=12 output=x1 > test.rsf bash$ < test.rsf sfdisfil 0: 0 2 4 6 8 5: 10 12 14 16 18 10: 20 22
The output format is easily configurable.
bash$ < test.rsf sfdisfil col=6 number=n format="%5.1f" 0.0 2.0 4.0 6.0 8.0 10.0 12.0 14.0 16.0 18.0 20.0 22.0
Along with sfdd, sfdisfil provides a simple way to convert RSF data to an ASCII form.
sfdottest
| Generic dot-product test for linear operators with adjoints | |||
|---|---|---|---|
| sfdottest mod=mod.rsf dat=dat.rsf > pip.rsf |
sfdottest is a generic dot-product test program for testing
linear operators. Suppose there is an executable program
<prog> that takes an RSF file from the standard input and
produces an RSF file in the standard output. It may take any number of
additional parameters but one of them must be adj= that sets
the forward (adj=0) or adjoint (adj=1) operations.
The program <prog> is typically an RSF program but it could
be anything (a script, a multiprocessor MPI program, etc.) as long as
it implements a linear operator and its adjoint
. The sfdottest program is testing the equality
by using random vectors and . You can invoke it with
bash$ sfdottest <prog> [optional aruments] mod=mod.rsf dat=dat.rsf
where mod.rsf and dat.rsf are RSF files that represent vectors from the model and data spaces. Pay attention to the dimension and size of these vectors! If the program does not respond for a very long time, it is quite possible that the dimension and size of the vectors are inconsistent with the requirement of the program to be tested. sfdottest does not create any temporary files and does not have any restrictive limitations on the size of the vectors. Here is an example. We first setup a vector with 100 elements using sfspike and then run sfdottest to test the sfcausint program. sfcausint implements a linear operator of causal integration and its adjoint, the anti-causal integration.
bash$ sfspike n1=100 > vec.rsf bash$ sfdottest sfcausint mod=vec.rsf dat=vec.rsf sfdottest: L[m]*d=1410.2 sfdottest: L'[d]*m=1410.2 bash$ sfdottest sfcausint mod=vec.rsf dat=vec.rsf sfdottest: L[m]*d=1165.87 sfdottest: L'[d]*m=1165.87
The numbers are different on subsequent runs because of changing seed in the random number generator. Here is a somewhat more complicated example. The sfhelicon program implements Claerbout's multidimensional helical filtering (Claerbout, 1998[2]). It requires a filter to be specified in addition to the input and output vectors. We create a helical 2-D filter using the Unix echo command.
bash$ echo 1 19 20 n1=3 n=20,20 data_format=ascii_int in=lag.rsf > lag.rsf bash$ echo 1 1 1 a0=-3 n1=3 data_format=ascii_float in=flt.rsf > flt.rsf
Next, we create an example 2-D model and data vector with sfspike.
bash$ sfspike n1=50 n2=50 > vec.rsf
Now the sfdottest program can perform the dot product test.
bash$ sfdottest sfhelicon filt=flt.rsf lag=lag.rsf \ > mod=vec.rsf dat=vec.rsf sfdottest: L[m]*d=8.97375 sfdottest: L'[d]*m=8.97375
Here is the same program tested in the inverse filtering mode:
bash$ sfdottest sfhelicon filt=flt.rsf lag=lag.rsf \ > mod=vec.rsf dat=vec.rsf div=y sfdottest: L[m]*d=15.0222 sfdottest: L'[d]*m=15.0222
sfget
| Output parameters from the header. | |||
|---|---|---|---|
| sfget < in.rsf parform=y par1 par2 ... | |||
| bool | parform=y | [y/n] | If y, print out parameter=value. If n, print out value. |
The sfget program extracts a parameter value from an RSF file. It is
useful mostly for scripting. Here is, for example, a quick calculation of the
maximum value on the first axis in an RSF dataset (the output of
sfspike) using the standard Unix bc calculator.
bash$ ( sfspike n1=100 | sfget n1 d1 o1; echo "o1+(n1-1)*d1" ) | bc .396
See also sfput.
Implementation: system/main/get.c
The implementation is trivial. Loop through all command-line parameters that contain the "=" character. <c>
for (i = 1; i < argc; i++) {
key = argv[i]; if (NULL != strchr(key,'=')) continue; </c>
Get the parameter value (as string) and output it as either key=value or value, depending on the parform parameter. <c> string = sf_histstring(in,key); if (NULL == string) { sf_warning("No key %s",key); } else { if (parform) printf ("%s=",key); printf("%s\n",string); } </c>
sfheadercut
| Zero a portion of a dataset based on a header mask. | |||
|---|---|---|---|
| sfheadercut mask=head.rsf < in.rsf > out.rsf | |||
The input data is a collection of traces n1xn2, mask is an integer array of size n2. |
sfheadercut is close to sfheaderwindow but instead
of windowing the dataset, it fills the traces specified by the header
mask with zeroes. The size of the input data is preserved.
Here is an example of using sfheaderwindow for
zeroing every other trace in the input file. First, let us create
an input file with ten traces:
bash$ sfmath n1=5 n2=10 output=x2+1 > input.rsf bash$ < input.rsf sfdisfil 0: 1 1 1 1 1 5: 2 2 2 2 2 10: 3 3 3 3 3 15: 4 4 4 4 4 20: 5 5 5 5 5 25: 6 6 6 6 6 30: 7 7 7 7 7 35: 8 8 8 8 8 40: 9 9 9 9 9 45: 10 10 10 10 10
Next, we can create a mask with alternating ones and zeros using sfinterleave.
bash$ sfspike n1=5 mag=1 | sfdd type=int > ones.rsf bash$ sfspike n1=5 mag=0 | sfdd type=int > zeros.rsf bash$ sfinterleave axis=1 ones.rsf zeros.rsf > mask.rsf bash$ sfdisfil < mask.rsf 0: 1 0 1 0 1 0 1 0 1 0
Finally, sfheadercut zeros the input traces.
bash$ sfheadercut < input.rsf mask=mask.rsf > output.rsf bash$ sfdisfil < output.rsf 0: 1 1 1 1 1 5: 0 0 0 0 0 10: 3 3 3 3 3 15: 0 0 0 0 0 20: 5 5 5 5 5 25: 0 0 0 0 0 30: 7 7 7 7 7 35: 0 0 0 0 0 40: 9 9 9 9 9 45: 0 0 0 0 0
sfheadersort
| Sort a dataset according to a header key. | |||
|---|---|---|---|
| sfheadersort < in.rsf > out.rsf head= | |||
| string | head= | header file | |
sfheadersort is used to sort traces in the input file
according to trace header information.
Here is an example of using
sfheadersort for randomly shuffling traces in the input
file. First, let us create an input file with seven traces:
bash$ sfmath n1=5 n2=7 output=x2+1 > input.rsf bash$ < input.rsf sfdisfil 0: 1 1 1 1 1 5: 2 2 2 2 2 10: 3 3 3 3 3 15: 4 4 4 4 4 20: 5 5 5 5 5 25: 6 6 6 6 6 30: 7 7 7 7 7
Next, we can create a random file with seven header values using sfnoise.
bash$ sfspike n1=7 | sfnoise rep=y type=n > random.rsf bash$ < random.rsf sfdisfil 0: 0.05256 -0.2879 0.1487 0.4097 0.1548 5: 0.4501 0.2836
If you reproduce this example, your numbers will most likely be different, because, in the absence of seed= parameter, sfnoise uses a random seed value to generate pseudo-random numbers. Finally, we apply sfheadersort to shuffle the input traces.
bash$ < input.rsf sfheadersort head=random.rsf > output.rsf bash$ < output.rsf sfdisfil 0: 2 2 2 2 2 5: 1 1 1 1 1 10: 3 3 3 3 3 15: 5 5 5 5 5 20: 7 7 7 7 7 25: 4 4 4 4 4 30: 6 6 6 6 6
As expected, the order of traces in the output file corresponds to the order of values in the header. Thanks to the separation between headers and data, the operation of sfheadersort is optimally efficient. It first sorts the headers and only then accesses the data, reading each data trace only once.
sfheaderwindow
| Window a dataset based on a header mask. | |||
|---|---|---|---|
| sfheaderwindow mask=head.rsf < in.rsf > out.rsf | |||
The input data is a collection of traces n1xn2, mask is an integer array os size n2, windowed is n1xm2, where m2 is the number of nonzero elements in mask. |
sfheaderwindow is used to window traces in the input file
according to trace header information.
Here is an example of using sfheaderwindow for randomly
selecting part of the traces in the input file. First, let us create
an input file with ten traces:
bash$ sfmath n1=5 n2=10 output=x2+1 > input.rsf bash$ < input.rsf sfdisfil 0: 1 1 1 1 1 5: 2 2 2 2 2 10: 3 3 3 3 3 15: 4 4 4 4 4 20: 5 5 5 5 5 25: 6 6 6 6 6 30: 7 7 7 7 7 35: 8 8 8 8 8 40: 9 9 9 9 9 45: 10 10 10 10 10
Next, we can create a random file with ten header values using sfnoise.
bash$ sfspike n1=10 | sfnoise rep=y type=n > random.rsf bash$ < random.rsf sfdisfil 0: -0.005768 0.02258 -0.04331 -0.4129 -0.3909 5: -0.03582 0.4595 -0.3326 0.498 -0.3517
If you reproduce this example, your numbers will most likely be different, because, in the absence of seed= parameter, sfnoise uses a random seed value to generate pseudo-random numbers. Finally, we apply sfheaderwindow to window the input traces selecting only those for which the header is greater than zero.
bash$ < random.rsf sfmask min=0 > mask.rsf bash$ < mask.rsf sfdisfil 0: 0 1 0 0 0 0 1 0 1 0 bash$ < input.rsf sfheaderwindow mask=mask.rsf > output.rsf bash$ < output.rsf sfdisfil 0: 2 2 2 2 2 5: 7 7 7 7 7 10: 9 9 9 9 9
In this case, only three traces are selected for the output. Thanks to the separation between headers and data, the operation of sfheaderwindow is optimally efficient.
sfin
| Display basic information about RSF files. | |||
|---|---|---|---|
| sfin info=y check=2. trail=y file1.rsf file2.rsf ... | |||
| n1,n2,... are data dimensions o1,o2,... are axis origins d1,d2,... are axis sampling intervals label1,label2,... are axis labels unit1,unit2,... are axis units | |||
| float | check=2. | Portion of the data (in Mb) to check for zero values. | |
| bool | info=y | [y/n] | If n, only display the name of the data file. |
| bool | trail=y | [y/n] | If n, skip trailing dimensions of one |
sfin is one of the most useful programs for operating with
RSF files. It produces quick information on the file hypercube
dimensions and checks the consistency of the associated data file.
Here is an example. Let us create an RSF file and examine it with sfin.
bash$ sfspike n1=100 n2=20 > spike.rsf
bash$ sfin spike.rsf
spike.rsf:
in="/tmp/spike.rsf@"
esize=4 type=float form=native
n1=100 d1=0.004 o1=0 label1="Time" unit1="s"
n2=20 d2=0.1 o2=0 label2="Distance" unit2="km"
2000 elements 8000 bytes
sfin reports the following information:
- location of the data file (/tmp/spike.rsf\@)
- element size (4 bytes)
- element type (floating point)
- element form (native)
- hypercube dimensions (100 by 20)
- axes scale (0.004 and 0.1)
- axes origin (0 and 0)
- axes labels
- axes units
- total number of elements
- total number of bytes in the data file
Suppose that the file got corrupted by a buggy program and reports incorrect dimensions. The sfin program should be able to catch the discrepancy.
bash$ echo n2=100 >> spike.rsf bash$ sfin spike.rsf > /dev/null sfin: Actually 8000 bytes, 20% of expected.
sfin also checks the first records in the file for zeros.
bash$ sfspike n1=100 n2=100 k2=99 > spike2.rsf bash$ sfin spike2.rsf >/dev/null sfin: The first 32768 bytes are all zeros
The number of bytes to check is adjustable
bash$ sfin spike2.rsf check=0.01 >/dev/null sfin: The first 16384 bytes are all zeros
You can also output only the location of the data file. This is sometimes handy in scripts.
bash$ sfin spike.rsf spike2.rsf info=n /tmp/spike.rsf@ /tmp/spike2.rsf@
An alternative is to use sfget, as follows:
bash$ sfget parform=n in < spike.rsf /tmp/spike.rsf@
To actually eliminate annoying trailing dimensions of length one (not just stop displaying them with trail=n), you may use sed. Example for eliminating axis 6: <bash> sed -i 's/n6=1//g' file.rsf </bash>
sfinterleave
| Combine several datasets by interleaving. | |||
|---|---|---|---|
| sfinterleave > out.rsf axis=3 [< file0.rsf] file1.rsf file2.rsf ... | |||
| int | axis=3 | Axis for interleaving | |
sfinterleave combines two or more datasets by interleaving them on one
of the axes. Here is a quick example:
bash$ sfspike n1=5 n2=5 > one.rsf bash$ sfdisfil < one.rsf 0: 1 1 1 1 1 5: 1 1 1 1 1 10: 1 1 1 1 1 15: 1 1 1 1 1 20: 1 1 1 1 1 bash$ sfscale < one.rsf dscale=2 > two.rsf bash$ sfdisfil < two.rsf 0: 2 2 2 2 2 5: 2 2 2 2 2 10: 2 2 2 2 2 15: 2 2 2 2 2 20: 2 2 2 2 2 bash$ sfinterleave one.rsf two.rsf axis=1 | sfdisfil 0: 1 2 1 2 1 5: 2 1 2 1 2 10: 1 2 1 2 1 15: 2 1 2 1 2 20: 1 2 1 2 1 25: 2 1 2 1 2 30: 1 2 1 2 1 35: 2 1 2 1 2 40: 1 2 1 2 1 45: 2 1 2 1 2 bash$ sfinterleave < one.rsf two.rsf axis=2 | sfdisfil 0: 1 1 1 1 1 5: 2 2 2 2 2 10: 1 1 1 1 1 15: 2 2 2 2 2 20: 1 1 1 1 1 25: 2 2 2 2 2 30: 1 1 1 1 1 35: 2 2 2 2 2 40: 1 1 1 1 1 45: 2 2 2 2 2
sfmask
| Create a mask. | |||
|---|---|---|---|
| sfmask < in.rsf > out.rsf min=-FLT_MAX max=+FLT_MAX | |||
Mask is an integer data with ones and zeros. Ones correspond to input values between min and max. The output can be used with sfheaderwindow. | |||
| float | max=+FLT_MAX | maximum header value | |
| float | min=-FLT_MAX | minimum header value | |
sfmask creates an integer output of ones and zeros comparing
the values of the input data to specified min= and
max= parameters. It is useful for sfheaderwindow and
in many other applications. Here is a quick example:
bash$ sfmath n1=10 output="sin(x1)" > sin.rsf bash$ < sin.rsf sfdisfil 0: 0 0.8415 0.9093 0.1411 -0.7568 5: -0.9589 -0.2794 0.657 0.9894 0.4121 bash$ < sin.rsf sfmask min=-0.5 max=0.5 | sfdisfil 0: 1 0 0 1 0 0 1 0 0 1
sfmath
| Mathematical operations on data files. | |||
|---|---|---|---|
| sfmath > out.rsf n#= d#=(1,1,...) o#=(0,0,...) label#= unit#= type= label= unit= output= | |||
Known functions: cos, sin, tan, acos, asin, atan, cosh, sinh, tanh, acosh, asinh, atanh, exp, log, sqrt, abs, erf, erfc (for float data), arg, conj, real, imag (for complex data). sfmath will work on float or complex data, but all the input and output files must be of the same data type. An alternative to sfmath is sfadd, which may be more efficient, but is less versatile. Examples: sfmath x=file1.rsf y=file2.rsf power=file3.rsf output='sin((x+2*y)^power)' > out.rsf sfmath < file1.rsf tau=file2.rsf output='exp(tau*input)' > out.rsf sfmath n1=100 type=complex output="exp(I*x1)" > out.rsf Arguments which are not treated as variables in mathematical expressions: datapath=, type=, out= See also: sfheadermath. | |||
| float | d#=(1,1,...) | sampling on #-th axis | |
| string | label= | data label | |
| string | label#= | label on #-th axis | |
| largeint | n#= | size of #-th axis | |
| float | o#=(0,0,...) | origin on #-th axis | |
| string | output= | Mathematical description of the output | |
| string | type= | output data type [float,complex] | |
| string | unit= | data unit | |
| string | unit#= | unit on #-th axis | |
sfmath is a versatile program for mathematical operations with RSF files. It can operate with several input files, all of the same dimensions and data type. The data type can be real (floating point) or complex. Here is an example that demonstrates several features of sfmath.
bash$ sfmath n1=629 d1=0.01 o1=0 n2=40 d2=1 o2=5 \ output="x2*(8+sin(6*x1+x2/10))" > rad.rsf bash$ < rad.rsf sfrtoc | sfmath output="input*exp(I*x1)" > rose.rsf bash$ < rose.rsf sfgraph title=Rose screenratio=1 wantaxis=n | sfpen
The first line creates a 2-D dataset that consists of 40 traces 629 samples each. The values of the data are computed with the formula "x2*(8+sin(6*x1+x2/10))", where x1 refers to the coordinate on the first axis, and x2 is the coordinate of the second axis. In the second line, we convert the data from real to complex using sfrtoc and produce a complex dataset using formula "input*exp(I*x1)", where input refers to the input file. Finally, we plot the complex data as a collection of parametric curves using sfgraph and display the result using sfpen. The plot appearing on your screen should look similar to the figure.

One possible alternative to the second line above is
bash$ < rad.rsf sfmath output=x1 > ang.rsf bash$ sfmath r=rad.rsf a=ang.rsf output="r*cos(a)" > cos.rsf bash$ sfmath r=rad.rsf a=ang.rsf output="r*sin(a)" > sin.rsf bash$ sfcmplx cos.rsf sin.rsf > rose.rsf
Here we refer to input files by names (r and a) and combine the names in a formula.
Functions can be nested and combined, and variable names, as well as the the input keyword may be combined with the axes keywords x1, x2, etc. Here is an example that shifts a wavelet -0.4s to t=0, computes the frequency-domain complex square root (equivalent to the convolutional square root in time), and shifts the result back to t=0.4s: <bash> pi=3.14159265 tshift=0.4
sfspike n1=256 k1=101 |\ sfbandpass flo=4 fhi=30 |\ sffft1 opt=n sym=y |\ sfmath output="sqrt(input*exp(2*$pi*$tshift*x1*I))*exp(-2*$pi*$tshift*x1*I)" |\ sffft1 opt=n sym=y inv=y |\ sfgraph |\ sfpen </bash>
sfpad
| Pad a dataset with zeros. | |||
|---|---|---|---|
| sfpad < in.rsf > out.rsf beg#=0 end#=0 n#= | |||
n#out is equivalent to n#, both of them overwrite end#. | |||
| int | beg#=0 | the number of zeros to add before the beginning of #-th axis | |
| int | end#=0 | the number of zeros to add after the end of #-th axis | |
| int | n#= | the output length of #-th axis - padding at the end | |
sfpad increases the dimensions of the input dataset by padding the data with zeroes. Here are some simple examples.
bash$ sfspike n1=5 n2=3 > one.rsf bash$ sfdisfil < one.rsf 0: 1 1 1 1 1 5: 1 1 1 1 1 10: 1 1 1 1 1 bash$ < one.rsf sfpad n2=5 | sfdisfil 0: 1 1 1 1 1 5: 1 1 1 1 1 10: 1 1 1 1 1 15: 0 0 0 0 0 20: 0 0 0 0 0 bash$ < one.rsf sfpad beg2=2 | sfdisfil 0: 0 0 0 0 0 5: 0 0 0 0 0 10: 1 1 1 1 1 15: 1 1 1 1 1 20: 1 1 1 1 1 bash$ < one.rsf sfpad beg2=1 end2=1 | sfdisfil 0: 0 0 0 0 0 5: 1 1 1 1 1 10: 1 1 1 1 1 15: 1 1 1 1 1 20: 0 0 0 0 0 bash$ < one.rsf sfwindow n1=3 | sfpad n1=5 n2=5 beg1=1 beg2=1 | sfdisfil 0: 0 0 0 0 0 5: 0 1 1 1 0 10: 0 1 1 1 0 15: 0 1 1 1 0 20: 0 0 0 0 0
You can use sfcat to pad data with values other than zeroes.
sfput
| Input parameters into a header. | |||
|---|---|---|---|
| sfput < in.rsf > out.rsf [parameter=value list] |
sfput is a very simple program. It simply appends parameters
from the command line to the output RSF file. One can achieve similar
results with editing the file by hand or with standard Unix utilities like
sed and echo. sfput is sometimes more
convenient because it handles input/output operations similarly to
other Madagascar programs.
bash$ sfspike n1=10 > spike.rsf
bash$ sfin spike.rsf
spike.rsf:
in="/tmp/spike.rsf@"
esize=4 type=float form=native
n1=10 d1=0.004 o1=0 label1="Time" unit1="s"
10 elements 40 bytes
bash$ sfput < spike.rsf d1=25 label1=Depth unit1=m > spike2.rsf
bash$ sfin spike2.rsf
spike2.rsf:
in="/tmp/spike2.rsf@"
esize=4 type=float form=native
n1=10 d1=25 o1=0 label1="Depth" unit1="m"
10 elements 40 bytes
sfreal
| Extract real (sfreal) or imaginary (sfimag) part of a complex dataset. | |||
|---|---|---|---|
| sfreal < cmplx.rsf > real.rsf |
sfreal extracts the real part of a complex type dataset. The
imaginary part can be extracted with sfimag, an the real
and imaginary part can be combined together with sfcmplx.
Here is a simple example. Let us first create a complex dataset
with sfmath
bash$ sfmath n1=10 type=complex output="(2+I)*x1" > cmplx.rsf bash$ fdisfil < cmplx.rsf 0: 0, 0i 2, 1i 4, 2i 3: 6, 3i 8, 4i 10, 5i 6: 12, 6i 14, 7i 16, 8i 9: 18, 9i
Extracting the real part with sfreal:
bash$ sfreal < cmplx.rsf | sfdisfil 0: 0 2 4 6 8 5: 10 12 14 16 18
Extracting the imaginary part with sfimag:
bash$ sfimag < cmplx.rsf | sfdisfil 0: 0 1 2 3 4 5: 5 6 7 8 9
sfreverse
| Reverse one or more axes in the data hypercube. | |||
|---|---|---|---|
| sfreverse < in.rsf > out.rsf which=-1 verb=false memsize=sf_memsize() opt= | |||
| int | memsize=sf_memsize() | Max amount of RAM (in Mb) to be used | |
| string | opt= | If y, change o and d parameters on the reversed axis;
| |
| bool | verb=n | [y/n] | Verbosity flag |
| int | which=-1 | Which axis to reverse.
| |
Here is an example of using sfreverse. First, let us create a 2-D dataset.
bash$ sfmath n1=5 d1=1 n2=3 d2=1 output=x1+x2 > test.rsf bash$ < test.rsf sfdisfil 0: 0 1 2 3 4 5: 1 2 3 4 5 10: 2 3 4 5 6
Reversing the first axis:
bash$ < test.rsf sfreverse which=1 | sfdisfil 0: 4 3 2 1 0 5: 5 4 3 2 1 10: 6 5 4 3 2
Reversing the second axis:
bash$ < test.rsf sfreverse which=2 | sfdisfil 0: 2 3 4 5 6 5: 1 2 3 4 5 10: 0 1 2 3 4
Reversing both the first and the second axis:
bash$ < test.rsf sfreverse which=3 | sfdisfil 0: 2 3 4 5 6 5: 1 2 3 4 5 10: 0 1 2 3 4
As you can see, the which= parameter controls the axes that are being reversed by encoding them into one number. When an axis is reversed, what happens with its axis origin and sampling parameters? This behavior is controlled by opt=. In our example,
bash$ < test.rsf sfget n1 o1 d1 n1=5 o1=0 d1=1 bash$ < test.rsf sfreverse which=1 | sfget o1 d1 o1=4 d1=-1
The default behavior (equivalent to opt=y) puts the origin o1 at the end of the axis and reverses the sampling parameter d1. Using opt=n preserves the sampling but reverses the origin.
bash$ < test.rsf sfreverse which=1 opt=n | sfget o1 d1 o1=-4 d1=1
Using opt=i preserves both the sampling and the origin while reversing the axis.
bash$ < test.rsf sfreverse which=1 opt=i | sfget o1 d1 o1=0 d1=1
One of the three possible behaviors may be desirable depending on the application.
sfrm
| Remove RSF files together with their data. | |||
|---|---|---|---|
| sfrm file1.rsf [file2.rsf ...] [-i] [-v] [-f] | |||
| Mimics the standard Unix rm command. See also: sfmv, sfcp. |
sfrm is a program for removing RSF files. Its arguments mimic the arguments of the standard Unix rm utility: -v for verbosity, -i for interactive inquiry, -f for force removal of suspicious files. Unlike the Unix rm, sfrm removes both the RSF header files and the binary files that the headers point to. Example:
bash$ sfspike n1=10 > spike.rsf datapath=./ bash$ sfget in < spike.rsf in=./spike.rsf@ bash$ ls spike* spike.rsf spike.rsf@ bash$ sfrm -v spike.rsf sfrm: sf_rm: Removing header spike.rsf sfrm: sf_rm: Removing data ./spike.rsf@ bash$ ls spike* ls: No match.
sfrotate
| Rotate a portion of one or more axes in the data hypercube. | |||
|---|---|---|---|
| sfrotate < in.rsf > out.rsf verb=n memsize=sf_memsize() rot#=(0,0,...) | |||
| int | memsize=sf_memsize() | Max amount of RAM (in Mb) to be used | |
| int | rot#=(0,0,...) | length of #-th axis that is moved to the end | |
| bool | verb=n | [y/n] | Verbosity flag |
sfrotate modifies the input dataset by splitting it into parts and putting the parts back in a different order. Here is a quick example.
bash$ sfmath n1=5 d1=1 n2=3 d2=1 output=x1+x2 > test.rsf bash$ < test.rsf sfdisfil 0: 0 1 2 3 4 5: 1 2 3 4 5 10: 2 3 4 5 6
Rotating the first axis by putting the last two columns in front:
bash$ < test.rsf sfrotate rot1=2 | sfdisfil 0: 3 4 0 1 2 5: 4 5 1 2 3 10: 5 6 2 3 4
Rotating the second axis by putting the last row in front:
bash$ < test.rsf sfrotate rot2=1 | sfdisfil 0: 2 3 4 5 6 5: 0 1 2 3 4 10: 1 2 3 4 5
Rotating both the first and the second axis:
bash$ < test.rsf sfrotate rot1=3 rot2=1 | sfdisfil 0: 4 5 6 2 3 5: 2 3 4 0 1 10: 3 4 5 1 2
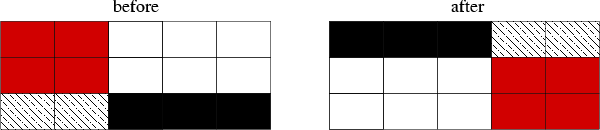
The transformation is shown schematically in Figure~(fig:rotate).
sfrtoc
| Convert real data to complex (by adding zero imaginary part). | |||
|---|---|---|---|
| sfrtoc < real.rsf > cmplx.rsf | |||
See also: sfcmplx |
The input to sfrtoc can be any type=float dataset:
bash$ sfspike n1=10 n2=20 n3=30 >real.rsf
bash$ sfin real.rsf
real.rsf:
in="/var/tmp/real.rsf@"
esize=4 type=float form=native
n1=10 d1=0.004 o1=0 label1="Time" unit1="s"
n2=20 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=30 d3=0.1 o3=0 label3="Distance" unit3="km"
6000 elements 24000 bytes
The output dataset will have type=complex, and its binary will be twice the size of the input:
bash$ <real.rsf sfrtoc >complex.rsf
bash$ sfin complex.rsf
complex.rsf:
in="/var/tmp/complex.rsf@"
esize=8 type=complex form=native
n1=10 d1=0.004 o1=0 label1="Time" unit1="s"
n2=20 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=30 d3=0.1 o3=0 label3="Distance" unit3="km"
6000 elements 48000 bytes
sfscale
| Scale data. | |||
|---|---|---|---|
| sfscale < in.rsf > out.rsf axis=0 rscale=0. dscale=1. | |||
To scale by a constant factor, you can also use sfmath or sfheadermath. | |||
| int | axis=0 | Scale by maximum in the dimensions up to this axis. | |
| float | dscale=1. | Scale by this factor (works if rscale=0) | |
| float | rscale=0. | Scale by this factor. | |
sfscale scales the input dataset by a factor. Here are some simple examples. First, let us create a test dataset.
bash$ sfmath n1=5 n2=3 o1=1 o2=1 output="x1*x2" > test.rsf bash$ < test.rsf sfdisfil 0: 1 2 3 4 5 5: 2 4 6 8 10 10: 3 6 9 12 15
Scale every data point by 2:
bash$ < test.rsf sfscale dscale=2 | sfdisfil 0: 2 4 6 8 10 5: 4 8 12 16 20 10: 6 12 18 24 30
Divide every trace by its maximum value:
bash$ < test.rsf sfscale axis=1 | sfdisfil 0: 0.2 0.4 0.6 0.8 1 5: 0.2 0.4 0.6 0.8 1 10: 0.2 0.4 0.6 0.8 1
Divide by the maximum value in the whole 2-D dataset:
bash$ < test.rsf sfscale axis=2 | sfdisfil 0: 0.06667 0.1333 0.2 0.2667 0.3333 5: 0.1333 0.2667 0.4 0.5333 0.6667 10: 0.2 0.4 0.6 0.8 1
The rscale= parameter is synonymous to dscale= except when it is equal to zero. With sfscale dscale=0, the dataset gets multiplied by zero. If using rscale=0, the other parameters are used to define scaling. Thus, sfscale rscale=0 axis=1 is equivalent to sfscale axis=1, and sfscale rscale=0 is equivalent to sfscale dscale=1.
sfspike
| Generate simple data: spikes, boxes, planes, constants. | |||
|---|---|---|---|
| sfspike > spike.rsf mag= nsp=1 k#=[0,...] l#=[k1,k2,...] p#=[0,...] n#= o#=[0,0,...] d#=[0.004,0.1,0.1,...] label#=[Time,Distance,Distance,...] unit#=[s,km,km,...] title= | |||
Spike positioning is given in samples and starts with 1. | |||
| float | d#=[0.004,0.1,0.1,...] | sampling on #-th axis | |
| ints | k#=[0,...] | spike starting position [nsp] | |
| ints | l#=[k1,k2,...] | spike ending position [nsp] | |
| string | label#=[Time,Distance,Distance,...] | label on #-th axis | |
| floats | mag= | spike magnitudes [nsp] | |
| int | n#= | size of #-th axis | |
| int | nsp=1 | Number of spikes | |
| float | o#=[0,0,...] | origin on #-th axis | |
| floats | p#=[0,...] | spike inclination (in samples) [nsp] | |
| string | title= | title for plots | |
| string | unit#=[s,km,km,...] | unit on #-th axis | |
sfspike takes no input and generates an output with "spikes". It is an easy way to create data. Here is an example:
bash$ sfspike n1=5 n2=3 k1=4 k2=1 | sfdisfil 0: 0 0 0 1 0 5: 0 0 0 0 0 10: 0 0 0 0 0
The spike location is specified by parameters k1=4 and k2=1. Note that the locations are numbered starting from 1. If one of the parameters is omitted or given the value of zero, the spike in the corresponding direction becomes a plane:
bash$ sfspike n1=5 n2=3 k1=4 | sfdisfil 0: 0 0 0 1 0 5: 0 0 0 1 0 10: 0 0 0 1 0
If no spike parameters are given, the whole dataset is filled with ones:
bash$ sfspike n1=5 n2=3 | sfdisfil 0: 1 1 1 1 1 5: 1 1 1 1 1 10: 1 1 1 1 1
To create several spikes, use the nsp= parameter and give a comma-separated list of values to k#= arguments:
bash$ sfspike n1=5 n2=3 nsp=3 k1=1,3,4 k2=1,2,3 | sfdisfil 0: 1 0 0 0 0 5: 0 0 1 0 0 10: 0 0 0 1 0
If the number of values in the list is smaller than nsp, the last value gets repeated, and the spikes add on top of each other, creating larger amplitudes:
bash$ sfspike n1=5 n2=3 nsp=3 k1=1,3 k2=1,2 | sfdisfil 0: 1 0 0 0 0 5: 0 0 2 0 0 10: 0 0 0 0 0
The magnitude of the spikes can be controlled explicitly with the mag= parameter:
bash$ sfspike n1=5 n2=3 nsp=3 k1=1,3,4 k2=1,2,3 mag=1,4,2 | sfdisfil 0: 1 0 0 0 0 5: 0 0 4 0 0 10: 0 0 0 2 0
You can create boxes instead of spikes by using l#= parameters:
bash$ sfspike n1=5 n2=3 k1=2 l1=4 k2=2 mag=8 | sfdisfil 0: 0 0 0 0 0 5: 0 8 8 8 0 10: 0 0 0 0 0
In this case, k1=2 specifies the box start, and l1=4 specifies the box end. Finally, multi-dimensional planes can be given an inclination by using p#= parameters:
bash$ sfspike n1=5 n2=3 k1=2 p2=1 | sfdisfil 0: 0 1 0 0 0 5: 0 0 1 0 0 10: 0 0 0 1 0
Note that sfspike interprets the p#= parameters in stepout from sample to sample, not in terms of axes units (i.e. s/m).
More than one p parameter can be specified. In this case, a (hyper) plane will be created.
When the inclination value is not integer, simple linear interpolation is used:
bash$ sfspike n1=5 n2=3 k1=2 p2=0.7 | sfdisfil 0: 0 1 0 0 0 5: 0 0.3 0.7 0 0 10: 0 0 0.6 0.4 0
sfspike supplies default dimensions and labels to all axis:
bash$ sfspike n1=5 n2=3 n3=4 > spike.rsf
bash$ sfin spike.rsf
spike.rsf:
in="/var/tmp/spike.rsf@"
esize=4 type=float form=native
n1=5 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=4 d3=0.1 o3=0 label3="Distance" unit3="km"
60 elements 240 bytes
As you can see, the first axis is assumed to be time, with sampling of seconds. All other axes are assumed to be distance, with sampling of kilometers. All these parameters can be changed on the command line.
bash$ sfspike n1=5 n2=3 n3=4 label3=Offset unit3=ft d3=20 > spike.rsf
bash$ sfin spike.rsf
spike.rsf:
in="/var/tmp/spike.rsf@"
esize=4 type=float form=native
n1=5 d1=0.004 o1=0 label1="Time" unit1="s"
n2=3 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=4 d3=20 o3=0 label3="Offset" unit3="ft"
60 elements 240 bytes
sfspray
| Extend a dataset by duplicating in the specified axis dimension. | |||
|---|---|---|---|
| sfspray < in.rsf > out.rsf axis=2 n= d= o= label= unit= | |||
| This operation is adjoint to sfstack. | |||
| int | axis=2 | which axis to spray | |
| float | d= | Sampling of the newly created dimension | |
| string | label= | Label of the newly created dimension | |
| int | n= | Size of the newly created dimension | |
| float | o= | Origin of the newly created dimension | |
| string | unit= | Units of the newly created dimension | |
sfspray extends the input hypercube by replicating the data in one of the dimensions. The output dataset acquires one additional dimension. Here is an example: Start with a 2-D dataset
bash$ sfmath n1=5 n2=2 output=x1+x2 > test.rsf
bash$ sfin test.rsf
test.rsf:
in="/var/tmp/test.rsf@"
esize=4 type=float form=native
n1=5 d1=1 o1=0
n2=2 d2=1 o2=0
10 elements 40 bytes
bash$ < test.rsf sfdisfil
0: 0 1 2 3 4
5: 1 2 3 4 5
Extend the data in the second dimension
bash$ < test.rsf sfspray axis=2 n=3 > test2.rsf
bash$ sfin test2.rsf
test2.rsf:
in="/var/tmp/test2.rsf@"
esize=4 type=float form=native
n1=5 d1=1 o1=0
n2=3 d2=1 o2=0
n3=2 d3=1 o3=0
30 elements 120 bytes
bash$ < test2.rsf sfdisfil
0: 0 1 2 3 4
5: 0 1 2 3 4
10: 0 1 2 3 4
15: 1 2 3 4 5
20: 1 2 3 4 5
25: 1 2 3 4 5
The output is three-dimensional, with traces from the original data duplicated along the second axis. Extend the data in the third dimension
bash$ < test.rsf sfspray axis=3 n=2 > test3.rsf
bash$ sfin test3.rsf
test3.rsf:
in="/var/tmp/test3.rsf@"
esize=4 type=float form=native
n1=5 d1=1 o1=0
n2=2 d2=1 o2=0
n3=2 d3=? o3=?
20 elements 80 bytes
bash$ < test3.rsf sfdisfil
0: 0 1 2 3 4
5: 1 2 3 4 5
10: 0 1 2 3 4
15: 1 2 3 4 5
The output is also three-dimensional, with the original data replicated along the third axis.
sfstack
| Stack a dataset over one of the dimensions. | |||
|---|---|---|---|
| sfstack < in.rsf > out.rsf axis=2 rms=n norm=y min=n max=n | |||
This operation is adjoint to sfspray. | |||
| int | axis=2 | which axis to stack | |
| bool | max=n | [y/n] | If y, find maximum instead of stack. Ignores rms and norm. |
| bool | min=n | [y/n] | If y, find minimum instead of stack. Ignores rms and norm. |
| bool | norm=y | [y/n] | If y, normalize by fold. |
| bool | rms=n | [y/n] | If y, compute the root-mean-square instead of stack. |
While sfspray adds a dimension to a hypercube, sfstack effectively removes one of the dimensions by stacking over it. Here are some examples:
bash$ sfmath n1=5 n2=3 output=x1+x2 > test.rsf bash$ < test.rsf sfdisfil 0: 0 1 2 3 4 5: 1 2 3 4 5 10: 2 3 4 5 6 bash$ < test.rsf sfstack axis=2 | sfdisfil 0: 1.5 2 3 4 5 bash$ < test.rsf sfstack axis=1 | sfdisfil 0: 2.5 3 4
Why is the first value not 1 (in the first case) or 2 (in the second case)? By default, sfstack normalizes the stack by the fold (the number of non-zero entries). To avoid normalization, use norm=n, as follows:
bash$ < test.rsf sfstack norm=n | sfdisfil 0: 3 6 9 12 15
sfstack can also compute root-mean-square values as well as minimum and maximum values.
bash$ < test.rsf sfstack rms=y | sfdisfil 0: 1.581 2.16 3.109 4.082 5.066 bash$ < test.rsf sfstack min=y | sfdisfil 0: 0 1 2 3 4 bash$ < test.rsf sfstack axis=1 max=y | sfdisfil 0: 4 5 6
sftransp
| Transpose two axes in a dataset. | |||
|---|---|---|---|
| sftransp < in.rsf > out.rsf memsize=sf_memsize() plane= | |||
If you get a "Cannot allocate memory" error, give the program a memsize=1 command-line parameter to force out-of-core operation. | |||
| int | memsize=sf_memsize() | Max amount of RAM (in Mb) to be used | |
| int | plane= | Two-digit number with axes to transpose. The default is 12 | |
The sftransp program transposes the input hypercube exchanging the two axes specified by the plane= parameter.
bash$ sfspike n1=10 n2=20 n3=30 > orig123.rsf
bash$ sfin orig123.rsf
orig123.rsf:
in="/var/tmp/orig123.rsf@"
esize=4 type=float form=native
n1=10 d1=0.004 o1=0 label1="Time" unit1="s"
n2=20 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=30 d3=0.1 o3=0 label3="Distance" unit3="km"
6000 elements 24000 bytes
bash$ <orig123.rsf sftransp plane=23 >out132.rsf
bash$ sfin out132.rsf
out132.rsf:
in="/var/tmp/out132.rsf@"
esize=4 type=float form=native
n1=10 d1=0.004 o1=0 label1="Time" unit1="s"
n2=30 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=20 d3=0.1 o3=0 label3="Distance" unit3="km"
6000 elements 24000 bytes
bash$ <orig123.rsf sftransp plane=13 >out321.rsf
bash$ sfin out321.rsf
out321.rsf:
in="/var/tmp/out132.rsf@"
esize=4 type=float form=native
n1=30 d1=0.1 o1=0 label1="Distance" unit1="km"
n2=20 d2=0.1 o2=0 label2="Distance" unit2="km"
n3=10 d3=0.004 o3=0 label3="Time" unit3="s"
6000 elements 24000 bytes
sftransp tries to fit the dataset in memory to transpose it there but, if not enough memory is available, it performs a slower transpose out of core using disk operations. You can control the amount of available memory using the memsize= parameter or the RSFMEMSIZE environmental variable.
sfwindow
| Window a portion of the dataset. | |||
|---|---|---|---|
| sfwindow < in.rsf > out.rsf verb=n squeeze=y j#=(1,...) d#=(d1,d2,...) f#=(0,...) min#=(o1,o2,,...) n#=(0,...) max#=(o1+(n1-1)*d1,o2+(n1-1)*d2,,...) | |||
| float | d#=(d1,d2,...) | sampling in #-th dimension | |
| int | f#=(0,...) | window start in #-th dimension | |
| int | j#=(1,...) | jump in #-th dimension | |
| float | max#=(o1+(n1-1)*d1,o2+(n1-1)*d2,,...) | maximum in #-th dimension | |
| float | min#=(o1,o2,,...) | minimum in #-th dimension | |
| int | n#=(0,...) | window size in #-th dimension | |
| bool | squeeze=y | [y/n] | if y, squeeze dimensions equal to 1 to the end |
| bool | verb=n | [y/n] | Verbosity flag |
sfwindow is used to window a portion of the dataset. Here is
a quick example: Start by creating some data.
bash$ sfmath n1=5 n2=3 o1=1 o2=1 output="x1*x2" > test.rsf bash$ < test.rsf sfdisfil 0: 1 2 3 4 5 5: 2 4 6 8 10 10: 3 6 9 12 15
Now window the first two rows:
bash$ < test.rsf sfwindow n2=2 | sfdisfil 0: 1 2 3 4 5 5: 2 4 6 8 10
Window the first three columns:
bash$ < test.rsf sfwindow n1=3 | sfdisfil 0: 1 2 3 2 4 5: 6 3 6 9
Window the middle row:
bash$ < test.rsf sfwindow f2=1 n2=1 | sfdisfil 0: 2 4 6 8 10
You can interpret the f# and n# parameters as meaning "skip that many rows/columns" and "select that many rows/columns" correspondingly. Window the middle point in the dataset:
bash$ < test.rsf sfwindow f1=2 n1=1 f2=1 n2=1 | sfdisfil 0: 6
Window every other column:
bash$ < test.rsf sfwindow j1=2 | sfdisfil 0: 1 3 5 2 6 5: 10 3 9 15
Window every third column:
bash$ < test.rsf sfwindow j1=3 | sfdisfil 0: 1 4 2 8 3 5: 12
Alternatively, sfwindow can use the minimum and maximum parameters to select a window. In the following example, we are creating a dataset with sfspike and then windowing a portion of it between 1 and 2 seconds in time and sampled at 8 miliseconds.
bash$ sfspike n1=1000 n2=10 > spike.rsf
bash$ sfin spike.rsf
spike.rsf:
in="/var/tmp/spike.rsf@"
esize=4 type=float form=native
n1=1000 d1=0.004 o1=0 label1="Time" unit1="s"
n2=10 d2=0.1 o2=0 label2="Distance" unit2="km"
10000 elements 40000 bytes
bash$ < spike.rsf sfwindow min1=1 max1=2 d1=0.008 > window.rsf
bash$ sfin window.rsf
window.rsf:
in="/var/tmp/window.rsf@"
esize=4 type=float form=native
n1=126 d1=0.008 o1=1 label1="Time" unit1="s"
n2=10 d2=0.1 o2=0 label2="Distance" unit2="km"
1260 elements 5040 bytes
By default, sfwindow "squeezes" the hypercube dimensions that are equal to one toward the end of the dataset. Here is an example of taking a time slice:
bash$ < spike.rsf sfwindow n1=1 min1=1 > slice.rsf
bash$ sfin slice.rsf
slice.rsf:
in="/var/tmp/slice.rsf@"
esize=4 type=float form=native
n1=10 d1=0.1 o1=0 label1="Distance" unit1="km"
n2=1 d2=0.004 o2=1 label2="Time" unit2="s"
10 elements 40 bytes
You can change this behavior by specifying squeeze=n.
bash$ < spike.rsf sfwindow n1=1 min1=1 squeeze=n > slice.rsf
bash$ sfin slice.rsf
slice.rsf:
in="/var/tmp/slice.rsf@"
esize=4 type=float form=native
n1=1 d1=0.004 o1=1 label1="Time" unit1="s"
n2=10 d2=0.1 o2=0 label2="Distance" unit2="km"
10 elements 40 bytes
Seismic programs
Programs in this category are specific for operations on seismic data. The source files for these programs can be found under system/seismic in the Madagascar distribution.
sffkamo
| Computes Azimuth Move-Out (AMO) operator in the f-k log-stretch domain | |||
|---|---|---|---|
| sffkamo < in.rsf > out.rsf h1= h2= f1= f2= maxe=10. | |||
| float | f1= | input azimuth in degrees | |
| float | f2= | output azimuth in degrees | |
| float | h1= | input offset | |
| float | h2= | output offset | |
| float | maxe=10. | stability constraint | |
Sample workflow from SEP-110, 63-70 (2001), with the addition of a bandpass for the input:
Create input -- a (t,x,y) common-offset cube: <bash> sfspike \ n1=128 o1=0.4 d1=0.0032 k1=65 label1=t \ n2=256 o2=-1.536 d2=0.012 k2=129 label2=x \ n3=128 o3=-1.024 d3=0.016 k3=65 label3=y | \ sfbandpass flo=5 fhi=60 > spikebps.rsf </bash>
Apply log-stretch FFT: <bash> <spikebps.rsf sfstretch rule=L dens=4 |\ sffft1 |\ sffft3 axis=2 |\ sffft3 axis=3 > spikefft3.rsf </bash>
Compute AMO operator for a file of the dimensions of spikefft3.rsf. The only information taken from stdin are the n, o, d parameters: <bash> <spikefft3.rsf sffkamo h2=2 f2=10 h1=1.8 f1=30 >oper.rsf </bash>
Apply the operator by multiplication and fft back to (t, mx, my): <bash> < spikefft3.rsf sfadd mode=prod oper.rsf |\ sffft3 axis=3 inv=y |\ sffft3 axis=2 inv=y |\ sffft1 inv=y |\ sfstretch rule=L dens=4 inv=y > spikeamo.rsf </bash>
Prepare for 8-bit greyscale visualization: <bash> < spikeamo.rsf sfbyte pclip=100 gainpanel=a > spikebyte.rsf </bash>
Picture from the middle of the impulse response: <bash> <spikebyte.rsf sfgrey3 frame1=65 frame2=129 frame3=65 \ point1=0.333 title='AMO saddle, no f-k filter' | sfpen & </bash>
Picture illustrating the artifacts (i.e. need for f-k filter): <bash> < spikebyte.rsf sfgrey3 frame1=65 frame2=97 frame3=97 \ point1=0.333 title='No f-k filter' | sfpen & </bash>
Apply the f-k filter and (in this case) visualize: <bash> < spikeamo.rsf sffft1 |\ sffft3 axis=2 |\ sffft3 axis=3 |\ sfdipfilter v1=-2.5 v2=-1.5 v3=1.5 v4=2.5 taper=2 pass=0 dim=3 |\ sffft3 axis=3 inv=y |\ sffft3 axis=2 inv=y |\ sffft1 inv=y |\ sfbyte pclip=100 gainpanel=a |\ sfgrey3 frame1=65 frame2=97 frame3=97 point1=0.333 title='With f-k filter' |\ sfpen & </bash>
sfheaderattr
| Integer header attributes. | |||
|---|---|---|---|
| sfheaderattr < head.rsf | |||
Only nonzero values are reported. |
The sfheaderattr examines the contents of a trace header file, typically generated by sfsegyread. In the example below, we examine trace headers in the output of suplane, a program from Seismic Unix.
bash$ suplane > plane.su bash$ sfsegyread tape=plane.su su=y tfile=tfile.rsf > plane.rsf bash$ sfheaderattr < tfile.rsf ******************************************* 71 headers, 32 traces key[0]="tracl" min[0]=1 max[31]=32 mean=16.5 key[1]="tracr" min[0]=1 max[31]=32 mean=16.5 key[11]="offset" min[0]=400 max[31]=400 mean=400 key[38]="ns" min[0]=64 max[31]=64 mean=64 key[39]="dt" min[0]=4000 max[31]=4000 mean=4000 *******************************************
For different standard keywords, a minimum, maximum, and mean values are reported unless they are identically zero. This quick inspection can help in identifying meaningful keywords set in the data. The input data type must be int.
sfheadermath
| Mathematical operations, possibly on header keys. | |||
|---|---|---|---|
| sfheadermath < in.rsf > out.rsf memsize=sf_memsize() output= | |||
Known functions: cos, sin, tan, acos, asin, atan, cosh, sinh, tanh, acosh, asinh, atanh, exp, log, sqrt, abs See also sfmath. An addition operation can be performed by sfstack. | |||
| int | memsize=sf_memsize() | Max amount of RAM (in Mb) to be used | |
| string | output= | Describes the output in a mathematical notation. | |
sfheadermath is a versatile program for mathematical operations on rows of the input file. If the input file is an n1 by n2 matrix, the output will be a 1 by n2 matrix that contains one row made out of mathematical operations on the other rows. sfheadermath can identify a row by number or by a standard SEGY keyword. The latter is useful for processing headers extracted from SEGY or SU files. Here is an example. First, we create an SU file with suplane and convert it to RSF using sfsegyread.
bash$ suplane > plane.su bash$ sfsegyread tape=plane.su su=y tfile=tfile.rsf > plane.rsf
The trace header information is saved in tfile.rsf. It contains 71 headers for 32 traces in integer format.
bash$ sfin tfile.rsf
tfile.rsf:
in="/tmp/tfile.rsf@"
esize=4 type=int form=native
n1=71 d1=? o1=?
n2=32 d2=? o2=?
2272 elements 9088 bytes
Next, we will convert tfile.rsf to a floating-point format and run sfheadermath to create a new header.
bash$ < tfile.rsf sfdd type=float | \
sfheadermath myheader=1 output="sqrt(myheader+(2+10*offset^2))" > new.rsf
bash$ sfin new.rsf
new.rsf:
in="/tmp/new.rsf@"
esize=4 type=float form=native
n1=1 d1=? o1=?
n2=32 d2=? o2=?
32 elements 128 bytes
We defined "myheader" as being the row number 1 in the input (note that numbering starts with 0) and combined it with "offset", which is a standard SEGY keyword that denotes row number 11 (see the output of sfheaderattr above.) A variety of mathematical expressions can be defined in the output= string. The expression processing engine is shared with sfmath.
sfsegyheader
| Make a trace header file for segywrite. | |||
|---|---|---|---|
| sfsegyheader < in.rsf > out.rsf n1= d1= | |||
Use the output for tfile= argument in segywrite. | |||
| float | d1= | trace sampling | |
| int | n1= | number of samples in a trace | |
sfsegyread
| Convert a SEG-Y or SU dataset to RSF. | |||
|---|---|---|---|
| sfsegyread mask=msk.rsf > out.rsf tfile=hdr.rsf verb=n su= suxdr=n endian=y format=segyformat (bhead) ns=segyns (bhead) tape= read= hfile= bfile= | |||
Data headers and trace headers are separated from the data. "suread" is equivalent to "segyread su=y" SEGY key names: tracl: trace sequence number within line 0 tracr: trace sequence number within reel 4 fldr: field record number 8 tracf: trace number within field record 12 ep: energy source point number 16 cdp: CDP ensemble number 20 cdpt: trace number within CDP ensemble 24 trid: trace identification code: 1 = seismic data 2 = dead 3 = dummy 4 = time break 5 = uphole 6 = sweep 7 = timing 8 = water break 9---, N = optional use (N = 32,767) 28 nvs: number of vertically summed traces 30 nhs: number of horizontally summed traces 32 duse: data use: 1 = production 2 = test 34 offset: distance from source point to receiver group (negative if opposite to direction in which the line was shot) 36 gelev: receiver group elevation from sea level (above sea level is positive) 40 selev: source elevation from sea level (above sea level is positive) 44 sdepth: source depth (positive) 48 gdel: datum elevation at receiver group 52 sdel: datum elevation at source 56 swdep: water depth at source 60 gwdep: water depth at receiver group 64 scalel: scale factor for previous 7 entries with value plus or minus 10 to the power 0, 1, 2, 3, or 4 (if positive, multiply, if negative divide) 68 scalco: scale factor for next 4 entries with value plus or minus 10 to the power 0, 1, 2, 3, or 4 (if positive, multiply, if negative divide) 70 sx: X source coordinate 72 sy: Y source coordinate 76 gx: X group coordinate 80 gy: Y group coordinate 84 counit: coordinate units code: for previous four entries 1 = length (meters or feet) 2 = seconds of arc (in this case, the X values are unsigned longitude and the Y values are latitude, a positive value designates the number of seconds east of Greenwich or north of the equator 88 wevel: weathering velocity 90 swevel: subweathering velocity 92 sut: uphole time at source 94 gut: uphole time at receiver group 96 sstat: source static correction 98 gstat: group static correction 100 tstat: total static applied 102 laga: lag time A, time in ms between end of 240- byte trace identification header and time break, positive if time break occurs after end of header, time break is defined as the initiation pulse which maybe recorded on an auxiliary trace or as otherwise specified by the recording system 104 lagb: lag time B, time in ms between the time break and the initiation time of the energy source, may be positive or negative 106 delrt: delay recording time, time in ms between initiation time of energy source and time when recording of data samples begins (for deep water work if recording does not start at zero time) 108 muts: mute time--start 110 mute: mute time--end 112 ns: number of samples in this trace 114 dt: sample interval, in micro-seconds 116 gain: gain type of field instruments code: 1 = fixed 2 = binary 3 = floating point 4 ---- N = optional use 118 igc: instrument gain constant 120 igi: instrument early or initial gain 122 corr: correlated: 1 = no 2 = yes 124 sfs: sweep frequency at start 126 sfe: sweep frequency at end 128 slen: sweep length in ms 130 styp: sweep type code: 1 = linear 2 = cos-squared 3 = other 132 stas: sweep trace length at start in ms 134 stae: sweep trace length at end in ms 136 tatyp: taper type: 1=linear, 2=cos^2, 3=other 138 afilf: alias filter frequency if used 140 afils: alias filter slope 142 nofilf: notch filter frequency if used 144 nofils: notch filter slope 146 lcf: low cut frequency if used 148 hcf: high cut frequncy if used 150 lcs: low cut slope 152 hcs: high cut slope 154 year: year data recorded 156 day: day of year 158 hour: hour of day (24 hour clock) 160 minute: minute of hour 162 sec: second of minute 164 timbas: time basis code: 1 = local 2 = GMT 3 = other 166 trwf: trace weighting factor, defined as 1/2^N volts for the least sigificant bit 168 grnors: geophone group number of roll switch position one 170 grnofr: geophone group number of trace one within original field record 172 grnlof: geophone group number of last trace within original field record 174 gaps: gap size (total number of groups dropped) 176 otrav: overtravel taper code: 1 = down (or behind) 2 = up (or ahead) 178 cdpx: X coordinate of CDP 180 cdpy: Y coordinate of CDP 184 iline: in-line number 188 xline: cross-line number 192 shnum: shotpoint number 196 shsca: shotpoint scalar 200 tval: trace value meas. 202 tconst4: transduction const 204 tconst2: transduction const 208 tunits: transduction units 210 device: device identifier 212 tscalar: time scalar 214 stype: source type 216 sendir: source energy dir. 218 unknown: unknown 222 smeas4: source measurement 224 smeas2: source measurement 228 smeasu: source measurement unit 230 unass1: unassigned 232 unass2: unassigned 236 | |||
| string | bfile= | output binary data header file | |
| bool | endian=y | [y/n] | Whether to automatically estimate endianness or not |
| int | format=segyformat (bhead) | [1,2,3,5] | Data format. The default is taken from binary header.
|
| string | hfile= | output text data header file | |
| string | mask= | optional header mask for reading only selected traces (auxiliary input file name) | |
| int | ns=segyns (bhead) | Number of samples. The default is taken from binary header | |
| string | read= | what to read: h - header, d - data, b - both (default) | |
| bool | su= | [y/n] | y if input is SU, n if input is SEGY |
| bool | suxdr=n | [y/n] | y, SU has XDR support |
| string | tape= | input data | |
| string | tfile= | output trace header file (auxiliary output file name) | |
| bool | verb=n | [y/n] | Verbosity flag |
The SEG Y format is an open standard for the exchange of geophysical data. It is controlled by the non-profit SEG Technical Standards Committee. There are two versions of this standard: rev0 (1975)[3] and rev1 (2002)[4]. The implementation in sfsegyread is a mixture of rev0 (i.e. no checks for Extended Textual Headers) and rev1 (IEEE floating point format allowed for trace data samples).
A SEG-Y file as understood by sfsegyread contains a "Reel Identification Header" (3200 bytes in EBCDIC followed by 400 bytes in a binary encoding), followed by a number of "Trace Blocks". Each "Trace Block" contains a 240-byte "Trace Header" (binary) followed by "Trace Data" -- a sequence of ns samples. Binary values in both reel headers and trace headers are two's complement integers, either two bytes or four bytes long. There are no floating-point values defined in the headers. Trace Data samples can have various encodings, either floating point or integer, described further down, but they are all big-endian. To convert from SEG-Y to RSF, sfsegyread will strip the tape reel EBCDIC header and convert it to ASCII, will extract the reel binary header without changing it, and will put the trace headers into one RSF file, and the traces themselves on another.
SEG-Y Trace Headers
In the SEG-Y standard, only the first 180 bytes of the 240-byte trace header are defined; bytes 181-240 are reserved for non-standard header information, and these locations are increasingly used in modern SEG-Y files and its variants. The standard provides for a total of 71 4-byte and 2-byte predefined header words. These 71 standard words have defined lengths and byte offsets, and only these words and byte locations are read using segyread and output to the RSF header file with the tfile= option. The user may remap these predefined keywords to a different byte offsets.
SU File Format
An SU file is nothing more than a SEG-Y file without the reel headers, and with the Trace Data samples in the native encoding of the CPU the file was created on (Attention -- limited portability!). So, to convert from SU to RSF, sfsegyread will just separate headers and traces into two RSF files.
SEG-Y specific parameters
- hfile= specifies the name of the file in which the EBCDIC reel header will be put after conversion to ASCII. If you are certain there is no useful information in it, hfile=/dev/null works just fine. If you do not specify anything for this parameter you will get an ASCII file named header in the current directory. If you want to quickly preview this header before running sfsegyread, use
dd if=input.segy count=40 bs=80 cbs=80 conv=unblock,ascii
- bfile= specifies name of the file in which the binary reel header (the 400-bytes thing following the 3600-bytes EBCDIC) will be put without any conversion. The default name is "binary". Unless you have software that knows how to read exactly this special type of file, it will be completely useless, so do bfile=/dev/null
- format= specifies the format in which the trace data samples are in the SEG-Y input file. This is read from the binary reel header of the SEG-Y file. Valid values are 1(IBM floating point), 2 (4-byte integer), 3 (2-byte integer) and 5 (IEEE floating point). If the input file is SU, the format will be assumed to be the native float format.
- keyname= specifies the byte offset to remap a header using the trace header key names shown above. For example, if the CDP locations have been placed in bytes 181-184 instead of the standard 21-24, cdp=180 will remap the trace header to that location.
SU-specific parameters
- suxdr= specifies whether the input file was created with a SU package with XDR support enabled. If you have access to the source code of your SU install (try $CWPROOT/src), type: grep 'XDRFLAG =' $CWPROOT/src/Makefile.config and look at the last uncommented entry. If no value is given for XDRFLAG, the package was not compiled with XDR support.
Common parameters
- su= specifies if the input file is SU or SEG-Y. Default is su=n (SEG-Y file).
- tape= specifies the input data. Stdin could not be used because sfsegyread has to work with tapes, and needs to fseek back and forth through the input file. Thankfully, output is on stdout.
- read= specifies what parts of the "Trace Blocks" will be read. It can be read=d (only trace data is read), read=h (only trace headers are read) or read=b (both are read).
- tfile= gives the name of the RSF file to which trace headers are written. Obviously, it should be only specified with read=h or read=b.
- mask= is an optional parameter specifying the name of a mask that says which traces will be read. The mask is a 1-D RSF file with integers. The number of samples in the mask is the same as the number of traces in the unmasked SEG-Y. In places corresponding to unwanted traces there should be zeros in the mask.
- ns= specifies the number of samples in a trace. For SEG-Y files, the default is taken from the binary reel header, and for SU files, from the header of the first trace. This parameter is however critical enough that a command line override was given for it.
- verbose= is the verbosity flag. Can be y or n.
- endian= is a y/n flag (default y), specifying whether to automatically estimate or not if samples in the Trace Data blocks are big-endian or little-endian. Try it if you are in trouble and do not know what else to do, otherwise let the automatic estimation do its job.
sfsegywrite
| Convert an RSF dataset to SEGY or SU. | |||
|---|---|---|---|
| sfsegywrite < in.rsf tfile=hdr.rsf verb=false su=false endian=sf_endian() tape= hfile= bfile= | |||
Merges trace headers with data. | |||
| string | bfile= | input binary data header file | |
| bool | endian=sf_endian() | [y/n] | big/little endian flag. The default is estimated automatically |
| string | hfile= | input text data header file | |
| bool | su=n | [y/n] | y if output is SU, n if output is SEGY |
| string | tape= | ||
| bool | verb=n | [y/n] | Verbosity flag |
Please see sfsegyread for a complete description of parameter meanings and background issues. Parameters bfile and hfile should only be given values when the desired file is SEG-Y (default). The output file is specified by the tape= tag.
Generic programs
Programs in this category are general signal and image processing programs. The source files for these programs can be found under system/generic in the Madagascar distribution.
sfnoise
| Add random noise to the data. | |||
|---|---|---|---|
| sfnoise < in.rsf > out.rsf seed=time(NULL) type=y var= range= mean=0 rep=n | |||
| float | mean=0 | noise mean | |
| float | range= | noise range (default=1) | |
| bool | rep=n | [y/n] | if y, replace data with noise |
| int | seed=time(NULL) | random seed | |
| bool | type=y | [y/n] | noise distribution, y: normal, n: uniform |
| float | var= | noise variance | |
See the Program of the Month blog entry.
Plotting programs (stable)
The source files for these programs can be found under plot/main in the Madagascar distribution.
sfbox
| Draw a balloon-style label. | |||
|---|---|---|---|
| sfbox lab_color=VP_WHITE lab_fat=0 pscale=1. pointer=y reverse=n lat=0. long=90. angle=0. x0=0. y0=0. scale0=1. xt=2. yt=0. x_oval=0. y_oval=0. boxit=y length= scalet= size=.25 label= > out.vpl | |||
| float | angle=0. | longitude of floating label in 3-D | |
| bool | boxit=y | [y/n] | if y, create a box around text |
| int | lab_color=VP_WHITE | label color | |
| int | lab_fat=0 | label fatness | |
| string | label= | text for label | |
| float | lat=0. | ||
| float | length= | normalization for xt and yt | |
| float | long=90. | latitude and longitude of viewpoint in 3-D | |
| bool | pointer=y | [y/n] | if y, create arrow pointer |
| float | pscale=1. | scale factor for width of pointer | |
| bool | reverse=n | [y/n] | |
| float | scale0=1. | scale factor for x0 and y0 | |
| float | scalet= | ||
| float | size=.25 | text height in inches | |
| float | x0=0. | ||
| float | x_oval=0. | ||
| float | xt=2. | ||
| float | y0=0. | position of the pointer tip | |
| float | y_oval=0. | size of the oval around pointer | |
| float | yt=0. | relative position of text | |
sfcontour
| Contour plot. | |||
|---|---|---|---|
| sfcontour < in.rsf c= min1=o1 min2=o2 max1=o1+(n1-1)*d1 max2=o2+(n2-1)*d2 nc=50 dc= c0= transp=y minval= maxval= allpos=y barlabel= > plot.vpl | |||
| Run "sfdoc stdplot" for more parameters. | |||
| bool | allpos=y | [y/n] | contour positive values only |
| string | barlabel= | ||
| floats | c= | [nc] | |
| float | c0= | first contour | |
| float | dc= | contour increment | |
| float | max1=o1+(n1-1)*d1 | ||
| float | max2=o2+(n2-1)*d2 | data window to plot | |
| float | maxval= | maximum value for scalebar (default is the data maximum) | |
| float | min1=o1 | ||
| float | min2=o2 | ||
| float | minval= | minimum value for scalebar (default is the data minimum) | |
| int | nc=50 | number of contours | |
| bool | transp=y | [y/n] | if y, transpose the axes |
sfdots
| Plot signal with lollipops. | |||
|---|---|---|---|
| sfdots < in.rsf labels= dots=(n1 <= 130)? 1: 0 seemean=(bool) (n2 <= 30) strings=(bool) (n1 <= 400) connect=1 corners= silk=n gaineach=y labelsz=8 yreverse=n constsep=n seedead=n transp=n xxscale=1. yyscale=1. clip=-1. overlap=0.9 screenratio=VP_SCREEN_RATIO screenht=VP_STANDARD_HEIGHT screenwd=screenhigh / screenratio radius=dd1/3 label1= unit1= title= > plot.vpl | |||
| float | clip=-1. | data clip | |
| int | connect=1 | connection type: 1 - diagonal, 2 - bar, 4 - only for non-zero data | |
| bool | constsep=n | [y/n] | if y, use constant trace separation |
| int | corners= | number of polygon corners (default is 6) | |
| int | dots=(n1 <= 130)? 1: 0 | type of dots: 1 - baloon, 0 - no dots, 2 - only for non-zero data | |
| bool | gaineach=y | [y/n] | if y, gain each trace independently |
| string | label1= | ||
| strings | labels= | trace labels [n2] | |
| int | labelsz=8 | label size | |
| float | overlap=0.9 | trace overlap | |
| float | radius=dd1/3 | dot radius | |
| float | screenht=VP_STANDARD_HEIGHT | screen height | |
| float | screenratio=VP_SCREEN_RATIO | screen aspect ratio | |
| float | screenwd=screenhigh / screenratio | screen width | |
| bool | seedead=n | [y/n] | if y, show zero traces |
| bool | seemean=(bool) (n2 <= 30) | [y/n] | if y, draw axis lines |
| bool | silk=n | [y/n] | if y, silky plot |
| bool | strings=(bool) (n1 <= 400) | [y/n] | if y, draw strings |
| string | title= | ||
| bool | transp=n | [y/n] | if y, transpose the axis |
| string | unit1= | ||
| float | xxscale=1. | x scaling | |
| bool | yreverse=n | [y/n] | if y, reverse y axis |
| float | yyscale=1. | y scaling | |
sfgraph3
| Generate 3-D cube plot for surfaces. | |||
|---|---|---|---|
| sfgraph3 < in.rsf orient=1 min= max= point1=0.5 point2=0.5 frame1=0.5*(min+max) frame2=n1-1 frame3=0 movie=0 dframe=1 n1pix=n1/point1+n3/(1.-point1) n2pix=n2/point2+n3/(1.-point2) flat=y > plot.vpl | |||
| float | dframe=1 | frame increment in a movie | |
| bool | flat=y | [y/n] | if n, display perspective view |
| float | frame1=0.5*(min+max) | ||
| int | frame2=n1-1 | ||
| int | frame3=0 | frame numbers for cube faces | |
| float | max= | maximum function value | |
| float | min= | minimum function value | |
| int | movie=0 | 0: no movie, 1: movie over axis 1, 2: axis 2, 3: axis 3 | |
| int | n1pix=n1/point1+n3/(1.-point1) | number of vertical pixels | |
| int | n2pix=n2/point2+n3/(1.-point2) | number of horizontal pixels | |
| int | orient=1 | function orientation | |
| float | point1=0.5 | fraction of the vertical axis for front face | |
| float | point2=0.5 | fraction of the horizontal axis for front face | |
sfgraph
| Graph plot. | |||
|---|---|---|---|
| sfgraph < in.rsf symbolsz= pclip=100. transp=n symbol= > plot.vpl | |||
| Run "sfdoc stdplot" for more parameters. | |||
| float | pclip=100. | clip percentile | |
| string | symbol= | if set, plot with symbols instead of lines | |
| floats | symbolsz= | symbol size (default is 2) [n2] | |
| bool | transp=n | [y/n] | if y, transpose the axes |
sfgrey3
| Generate 3-D cube plot. | |||
|---|---|---|---|
| sfgrey3 < in.rsf point1=0.5 point2=0.5 frame1=0 frame2=n2-1 frame3=0 movie=0 dframe=1 n1pix=n1/point1+n3/(1.-point1) n2pix=n2/point2+n3/(1.-point2) flat=y scalebar=n minval= maxval= barreverse=n nreserve=8 bar= color= > plot.vpl | |||
| Requires an "unsigned char" input (the output of sfbyte). | |||
| string | bar= | file for scalebar data | |
| bool | barreverse=n | [y/n] | if y, go from small to large on the bar scale |
| string | color= | color scheme (default is i) | |
| int | dframe=1 | frame increment in a movie | |
| bool | flat=y | [y/n] | if n, display perspective view |
| int | frame1=0 | ||
| int | frame2=n2-1 | ||
| int | frame3=0 | frame numbers for cube faces | |
| float | maxval= | maximum value for scalebar (default is the data maximum) | |
| float | minval= | minimum value for scalebar (default is the data minimum) | |
| int | movie=0 | 0: no movie, 1: movie over axis 1, 2: axis 2, 3: axis 3 | |
| int | n1pix=n1/point1+n3/(1.-point1) | number of vertical pixels | |
| int | n2pix=n2/point2+n3/(1.-point2) | number of horizontal pixels | |
| int | nreserve=8 | reserved colors | |
| float | point1=0.5 | fraction of the vertical axis for front face | |
| float | point2=0.5 | fraction of the horizontal axis for front face | |
| bool | scalebar=n | [y/n] | if y, draw scalebar |
Different color schemes are available for sfgrey and sfgrey3. Examples are in the book at rsf/rsf/sfgrey.
sfgrey
| Generate raster plot. | |||
|---|---|---|---|
| sfgrey < in.rsf > out.rsf bar=bar.rsf transp=y yreverse=y xreverse=n gpow= phalf= clip= pclip= gainstep=0.5+n1/256. allpos=n bias=0. polarity=n verb=n scalebar=n minval= maxval= barreverse=n wantframenum=(bool) (n3 > 1) nreserve=8 gainpanel= bar= color= > (plot.vpl | char.rsf) | |||
| Can input char values. If called "byte", outputs char values. Run "sfdoc stdplot" for more parameters. | |||
| bool | allpos=n | [y/n] | if y, assume positive data |
| string | bar= | file for scalebar data | |
| bool | barreverse=n | [y/n] | if y, go from small to large on the bar scale |
| float | bias=0. | subtract bias from data | |
| float | clip= | ||
| string | color= | color scheme (default is i) | |
| string | gainpanel= | gain reference: 'a' for all, 'e' for each, or number | |
| int | gainstep=0.5+n1/256. | subsampling for gpow and clip estimation | |
| float | gpow= | ||
| float | maxval= | maximum value for scalebar (default is the data maximum) | |
| float | minval= | minimum value for scalebar (default is the data minimum) | |
| int | nreserve=8 | reserved colors | |
| float | pclip= | data clip percentile (default is 99) | |
| float | phalf= | percentage for estimating gpow | |
| bool | polarity=n | [y/n] | if y, reverse polarity (white is high by default) |
| bool | scalebar=n | [y/n] | |
| bool | transp=y | [y/n] | if y, transpose the display axes |
| bool | verb=n | [y/n] | verbosity flag |
| bool | wantframenum=(bool) (n3 > 1) | [y/n] | if y, display third axis position in the corner |
| bool | xreverse=n | [y/n] | if y, reverse the horizontal axis |
| bool | yreverse=y | [y/n] | if y, reverse the vertical axis |
Different color schemes are available and examples are in the book at rsf/rsf/sfgrey.
sfplas
| Plot Assembler - convert ascii to vplot. | |||
|---|---|---|---|
| sfplas |
sfpldb
| Plot Debugger - convert vplot to ascii. | |||
|---|---|---|---|
| sfpldb |
sfplotrays
| Plot rays. | |||
|---|---|---|---|
| sfplotrays frame=frame.rsf nt=n1*n2 jr=1 frame= < rays.rsf > plot.vpl | |||
| Run "sfdoc stdplot" for more parameters. | |||
| string | frame= | ||
| int | jr=1 | skip rays | |
| int | nt=n1*n2 | maximum ray length | |
sfthplot
| Hidden-line surface plot. | |||
|---|---|---|---|
| sfthplot < in.rsf uflag=y dflag=y alpha=45. titlsz=9 axissz=6 plotfat=0 titlefat=2 axisfat=2 plotcolup=VP_YELLOW plotcoldn=VP_RED axis=y axis1=y axis2=y axis3=y clip=0. pclip=100. gainstep=0.5+nx/256. bias=0. dclip=1. norm=y xc=1.5 zc=3 ratio=5. zmax= zmin= sz=6. label#= unit#= tpow=0 epow=0 gpow=1 title= > plot.vpl | |||
| float | alpha=45. | alpha| < 89 | |
| bool | axis=y | [y/n] | |
| bool | axis1=y | [y/n] | |
| bool | axis2=y | [y/n] | |
| bool | axis3=y | [y/n] | plot axis |
| int | axisfat=2 | axes fatness | |
| int | axissz=6 | axes size | |
| float | bias=0. | subtract bias from data | |
| float | clip=0. | data clip | |
| float | dclip=1. | change the clip: clip *= dclip | |
| bool | dflag=y | [y/n] | if y, plot down side of the surface |
| float | epow=0 | exponential gain | |
| int | gainstep=0.5+nx/256. | subsampling for gpow and clip estimation | |
| float | gpow=1 | power gain | |
| string | label#= | label on #-th axis | |
| bool | norm=y | [y/n] | normalize by the clip |
| float | pclip=100. | data clip percentile | |
| int | plotcoldn=VP_RED | color of the lower side | |
| int | plotcolup=VP_YELLOW | color of the upper side | |
| int | plotfat=0 | line fatness | |
| float | ratio=5. | plot adjustment | |
| float | sz=6. | vertical scale | |
| string | title= | ||
| int | titlefat=2 | title fatness | |
| int | titlsz=9 | title size | |
| string | tpow=0 | time power gain | |
| bool | uflag=y | [y/n] | if y, plot upper side of the surface |
| string | unit#= | unit on #-th axis | |
| float | xc=1.5 | ||
| float | zc=3 | lower left corner of the plot | |
| float | zmax= | ||
| float | zmin= | ||
sfwiggle
| Plot data with wiggly traces. | |||
|---|---|---|---|
| sfwiggle < in.rsf xpos=xpos.rsf xmax= xmin= poly=n fatp=1 xmask=1 ymask=1 pclip=98. zplot=0.75 clip=0. seemean=n verb=n transp=n yreverse=n xreverse=n xpos= > plot.vpl | |||
| Run "sfdoc stdplot" for more parameters. | |||
| float | clip=0. | data clip (estimated from pclip by default | |
| int | fatp=1 | ||
| float | pclip=98. | clip percentile | |
| bool | poly=n | [y/n] | |
| bool | seemean=n | [y/n] | if y, plot mean lines of traces |
| bool | transp=n | [y/n] | if y, transpose the axes |
| bool | verb=n | [y/n] | verbosity flag |
| int | xmask=1 | ||
| float | xmax= | maximum trace position (if using xpos) | |
| float | xmin= | minimum trace position (if using xpos) | |
| string | xpos= | optional header file with trace positions | |
| bool | xreverse=n | [y/n] | if y, reverse the horizontal axis |
| int | ymask=1 | ||
| bool | yreverse=n | [y/n] | if y, reverse the vertical axis |
| float | zplot=0.75 | ||
Plotting programs (development)
sfplsurf
sfplsurf utilizes PLplot's surface rendering capabilities. Output is dumped to stdout in VPLOT format, so it can easily be used in the same way as sfgrey or other plotting programs. It also supports animation, if n3 > 1 in the input file. A SConstruct usage example can be found below. A movie of the output is available as well.
from rsf.proj import *
# x & y dimensions
o1=-2
o2=-2
n1=41
n2=41
d1=0.1
d2=0.1
# z dimension
o3=-1
n3=21
d3=0.1
Flow('membrane',None,
'''
math o1=%g o2=%g n1=%d n2=%d d1=%g d2=%g
o3=%g n3=%d d3=%g
output="x3*cos(x1*x1+x2*x2)*exp(-0.1*(x1*x1+x2*x2))"
''' % (o1,o2,n1,n2,d1,d2,o3,n3,d3))
Result('membrane',
'''
plsurf title="Membrane" mesh=n color=j
minval=%g maxval=%g
''' % (o3,o3 + d3*(n3-1)))
End()system/generic programs
sfremap1
| 1-D ENO interpolation. | |||
|---|---|---|---|
| sfremap1 < in.rsf > out.rsf pattern=pattern.rsf n1=n1 d1=d1 o1=o1 order=3 | |||
| float | d1=d1 | Output sampling | |
| int | n1=n1 | Number of output samples | |
| float | o1=o1 | Output origin | |
| int | order=3 | Interpolation order | |
| string | pattern= | auxiliary input file name | |
To give an example of usage, we will create an input for sfremap1 with:
sfmath n1=11 n2=11 d1=1 d2=1 o1=-5 o2=-5 output="x1*x1+x2*x2" > inp2remap1.rsf
Let us interpolate the data across both dimensions, then display it:
< inp2remap1.rsf sfremap1 n1=1001 d1=0.01 | sftransp | \ sfremap1 n1=1001 d1=0.01 | sftransp | sfgrey allpos=y | sfpen
The comparison with the uninterpolated data ( < inp2remap1.rsf sfgrey allpos=y | sfpen ) is quite telling.
system/seismic programs
sfstretch
| Stretch of the time axis. | |||
|---|---|---|---|
| sfstretch < in.rsf > out.rsf datum=dat.rsf inv=n dens=1 v0= half=y delay= tdelay= hdelay= nout=dens*n1 extend=4 mute=0 maxstr=0 rule= | |||
| file | datum= | auxiliary input file name | |
| float | delay= | time delay for rule=lmo | |
| int | dens=1 | axis stretching factor | |
| int | extend=4 | trace extension | |
| bool | half=y | [y/n] | if y, the second axis is half-offset instead of full offset |
| float | hdelay= | offset delay for rule=rad | |
| bool | inv=n | [y/n] | if y, do inverse stretching |
| float | maxstr=0 | maximum stretch | |
| int | mute=0 | tapering size | |
| int | nout=dens*n1 | output axis length (if inv=n) | |
| string | rule= | Stretch rule:
| |
| float | tdelay= | time delay for rule=rad | |
| float | v0= | moveout velocity | |
sfstretch rule=d (aka sfdatstretch) can be used to apply statics. Here is a synthetic example, courtesy of Alessandro Frigeri:
# generate a dataset with 'flat' signals sfmath n1=200 n2=100 output="sin(0.5*x1)" type=float > scan.rsf # generate a sinusoidal elevation correction sfmath n1=100 output="3*sin(x1)" type=float > statics.rsf # apply statics, producing a 'wavy' output. sfstretch < scan.rsf > out.rsf datum=statics.rsf rule=d
user/fomels programs
sfpick
| Automatic picking from semblance-like panels. | |||
|---|---|---|---|
| sfpick < scn.rsf > pik.rsf vel0=o2 niter=100 an=1. gate=3 smooth=y rect#=(1,1,...) rect1=1 rect2=1 ... | |||
| rectN defines the size of the smoothing stencil in N-th dimension. Theory in Appendix B of: S. Fomel, 2009, Velocity analysis using AB semblance: Geophysical Prospecting, v. 57, 311-321. Reproducible version in RSFSRC/book/jsg/avo | |||
| float | an=1. | axes anisotropy | |
| int | gate=3 | picking gate | |
| int | niter=100 | number of iterations | |
| int | rect#=(1,1,...) | smoothing radius on #-th axis | |
| bool | smooth=y | [y/n] | if apply smoothing |
| float | vel0=o2 | surface velocity | |
Short description of the algorithm:
- Start from the top (first time slice), pick an initial (source) point, evaluate all other points with the direct traveltime.
- At each grid point at the next level, find the traveltime to points at the previous level, add the traveltimes from the previous level, and select minimum. The search radius is limited by the aperture (gate= parameter in sfpick).
- Repeat step 2 until reaching the bottom.
- Pick the minimum traveltime at the bottom and track the ray back to the source by following the traveltime gradient direction.
- Postprocessing (smooth= parameter in sfpick): smooth the picked ray path using shaping regularization.
The algorithm was discovered and rediscovered by many people. The best reference is probably V. Meshbey, E. Ragoza, D. Kosloff, U. Egozi, and D. Wexler, 2002, Three-dimensional Travel-time Calculation Based on Fermat's Principle: Pure and Applied Geophysics, v. 159, 1563-1582.
user/ivlad programs
sfprep4plot
| Resamples a 2-D dataset to the desired picture resolution, with antialias | |||
|---|---|---|---|
| sfprep4plot inp= out= verb=n h=none w=none unit= ppi= prar=y | |||
| Only one of the h and w parameters needs to be specified. If prar=n, no action will be taken on axis for which h/w was not specified If prar=y and only one par (h or w) is specified, the picture will scale along both axes until it is of the specified dimension. | |||
| int | h=none | output height | |
| string | inp= | input file | |
| string | out= | output file | |
| int | ppi= | output resolution (px/in). Necessary when unit!=px | |
| bool | prar=y | [y/n] | if y, PReserve Aspect Ratio of input |
| string | unit= | unit of h and w. Can be: px(default), mm, cm, in | |
| bool | verb=n | [y/n] | if y, print system commands, outputs |
| int | w=none | output width | |
For a figure that does not need the aspect ratio preserved, and needs to fill a 1280x1024 projector display:
sfprep4plot inp=file1.rsf out=file2.rsf w=1280 h=1024 prar=n
For a print figure that has to fit in a 6x8in box at a resolution of 250 dpi, preserving the aspect ratio:
sfprep4plot inp=file1.rsf out=file2.rsf w=6 h=8 unit=in ppi=250
A comparison of images before and after the application of sfprep4plot, courtesy of Joachim Mispel, is shown below:
sfcsv2rsf
| Convert a delimited-text ASCII file to RSF binary floating point or int. | |||
|---|---|---|---|
| sfcsv2rsf help=n delimiter=, dtype=float verb=n debug=n trunc=n o1=0. o2=0. d1=1. d2=1. unit1=unknown unit2=unknown label1=unknown label2=unknown | |||
| Zeros will be added if number of elements is not the same in each row. n1 and n2 are computed automatically. For consistency with sfdisfil and sfmatmult, output is C-style order (row-first), i.e. rows in input file become dimension-1 columns in output. Output encoding is native. | |||
| float | d1=1. | ||
| float | d2=1. | ||
| bool | debug=n | [y/n] | Extra verbosity for debugging |
| string | delimiter=, | Separator between values in input file | |
| string | dtype=float | Input type | |
| bool | help=n | [y/n] | |
| string | label1=unknown | ||
| string | label2=unknown | ||
| float | o1=0. | ||
| float | o2=0. | ||
| bool | trunc=n | [y/n] | Truncate or add zeros if nr elems in rows differs |
| string | unit1=unknown | ||
| string | unit2=unknown | ||
| bool | verb=n | [y/n] | Whether to echo n1, n2, infill/truncation |
A small usage example follow below. First, create an input file:
<bash> $ echo -e '5,6,8,9.2\n11,124,5,0,1' | tee file.csv 5,6,8,9.2 11,124,5,0,1 </bash>
You may notice that the number of values in each row is different.
Run sfcsv2rsf. Notice that no options are needed. By default, zeros will be appended to make the rows equal length:
<bash> $ <file.csv sfcsv2rsf > junk.rsf ; sfdisfil < junk.rsf
0: 5 6 8 9.2 0 5: 11 124 5 0 1
</bash>
Notice that sfdisfil displays in column order (i.e. matrix is transposed if the number of rows is right). The dimensions of the file are actually transposed on disk:
$ sfin junk.rsf junk.rsf:
in="/data/path/junk.rsf@" esize=4 type=float form=native n1=5 d1=1 o1=0 unit1="unknown" n2=2 d2=1 o2=0 unit2="unknown"
10 elements 40 bytes </bash>
You may want to run the output through sftransp, depending on your needs. However, if creating an input for sfmatmult, this will not be necessary, because sfmatmult is made to work with matrices that are displayed with sfdisfil, and takes as input a transpose matrix.
Pipes can be used, of course, to skip the creation of intermediary files:
<bash> $ <file.csv sfcsv2rsf | sfdisfil
0: 5 6 8 9.2 0 5: 11 124 5 0 1
</bash>
Note that since this program does not need any arguments (just stdin and stdout), when called with no arguments it will not display the man page. In order to consult the automatically generated documentation, you need to pass the option help=y .
user/jennings programs
sfsizes
| Display the size of RSF files. | |||
|---|---|---|---|
| sfsizes files=y human=n file1.rsf file2.rsf ... | |||
| Prints the element size, number of elements, and number of bytes for a list of RSF files. Non-RSF files are ignored. | |||
| bool | files=y | [y/n] | If y, print size of each file. If n, print only total. |
| bool | human=n | [y/n] | If y, print human-readable file size. If n, print byte count. |
This program computes the "theoretical" size in bytes of the data fork of RSF files. The actual space occupied on disk may be different and machine dependent due to disk blocking factors, etc. This theoretical array size should be reproducible. It is also fast because the program only reads the RSF headers files, not the actual data.
For example, to get the total size of all RSF files in a directory, in human readable format, without listing each file:
sfsizes files=n human=y *.rsf
This will also work because sfsizes simply skips any non-RSF file:
sfsizes files=n human=y *
sffiglist
| Compare Vplot files in Fig and Lock directories | |||
|---|---|---|---|
| sffiglist figdir= lockdir= list= show= | |||
|
Parameter figdir is path to Fig directory, default is ./Fig.
| |||
| string | figdir= | fig directory, default = ./Fig | |
| string | list= | how much to list [none,diff,miss,all], default = all | |
| string | lockdir= | lock directory, default = lock counterpart of figdir | |
| string | show= | how much to show [none,diff,miss,all], default = none | |
This tool lists Vplot files in "Fig" and "Lock" directories and compares them using sfvplotdiff.
The Fig directory defaults to ./Fig and the Lock directory defaults to the corresponding directory where "scons lock" puts things, but either default can be overridden with the user parameters figdir and lockdir so that, for example, files in two different Fig directories can be compared.
The default for the Lock directory has some logic to look in $RSFFIGS when Fig is in $RSFSRC/book, or to look in $RSFALTFIGS when Fig is not in $RSFSRC/book because I like to keep two different Lock directories: one for stuff in book and another for my own stuff that is not in book. However, I tried to make the code default to reasonable things if any of these environment variables are not defined.
The tool gives a summary count of files that are the same, files that are different, files in Fig that are missing from Lock, and files in Lock that are missing from Fig.
The parameters list (default=all) and show (default=none) control which files are listed or "flipped" with sfpen. The file listing indicates which files are the same, which are different, and which are missing from Fig or Lock.
For example, to list all the Vplot files in Fig and Lock:
sffiglist list=all
To list all Vplot files and flip only files that are different:
sffiglist list=all show=diff
user/psava programs
sfawefd2d
| acoustic time-domain FD modeling | |||
|---|---|---|---|
| sfawefd < Fwav.rsf vel=Fvel.rsf sou=Fsou.rsf rec=Frec.rsf wfl=Fwfl.rsf > Fdat.rsf den=Fden.rsf ompchunk=1 ompnth=0 verb=n snap=n free=n expl=n jdata=1 jsnap=nt nq1=sf_n(a1) nq2=sf_n(a2) oq1=sf_o(a1) oq2=sf_o(a2) | |||
| file | den= | auxiliary input file name | |
| bool | expl=n | [y/n] | "exploding reflector" |
| bool | free=n | [y/n] | free surface flag |
| int | jdata=1 | ||
| int | jsnap=nt | save wavefield every *jsnap* time steps | |
| int | nq1=sf_n(a1) | ||
| int | nq2=sf_n(a2) | ||
| int | ompchunk=1 | OpenMP data chunk size | |
| int | ompnth=0 | OpenMP available threads | |
| float | oq1=sf_o(a1) | ||
| float | oq2=sf_o(a2) | ||
| file | rec= | auxiliary input file name | |
| bool | snap=n | [y/n] | wavefield snapshots flag |
| file | sou= | auxiliary input file name | |
| file | vel= | auxiliary input file name | |
| bool | verb=n | [y/n] | verbosity flag |
| file | wfl= | auxiliary output file name | |
An example will be demonstrated below on a model with nx=nz=200, dx=dz=4m (size: 800x800m). There are two layers: the first one is 100x200 samples in (z,x) and the velocity is 1500m/s; the second layer has the same dimension and the velocity is 3000m/s. Density is set to 1 for the whole grid. A source and a receiver are co-located at x=400 and z=100. The full wavefield for the entire model aperture will be saved every 10th time step.
<bash>
- Velocity model:
sfspike >Fvel.rsf mag=1500,3000 nsp=2 k1=1,101 l1=100,200 d1=4 d2=4 \ label1=z label2=x n1=200 n2=200 o1=2 o2=2 unit1=m unit2=m
- Density model:
sfspike >Fden.rsf mag=1 nsp=1 k1=1 l1=200 d1=4 d2=4 label1=z \ label2=x n1=200 n2=200 o1=2 o2=2 unit1=m unit2=m
- Source position (x,z):
sfspike n1=2 nsp=2 k1=1,2 mag=400,100 o1=0 o2=0 >Fsou.rsf
- Receiver position (x,z):
sfspike n1=2 nsp=2 k1=1,2 mag=400,100 o1=0 o2=0 >Frec.rsf
- Source wavelet:
sfspike nsp=1 n1=2000 d1=0.0005 k1=200 | sfricker1 frequency=20 |\ sftransp >Fwav.rsf
- Creating data at specified receiver + saving full wavefield every 10th step:
sfawefd2d <Fwav.rsf vel=Fvel.rsf sou=Fsou.rsf rec=Frec.rsf wfl=Fwfl.rsf \ den=Fden.rsf >Fdat.rsf verb=y free=y expl=y snap=y dabc=y jdata=1 jsnap=10 echo 'label1=z unit1=m label2=x unit2=m' >> Fwfl.rsf
- View the wavefield movie:
< Fwfl.rsf sfgrey gainpanel=a pclip=99 color=j scalebar=y | sfpen
- View a wavefield snapshot:
< Fwfl.rsf sfwindow f3=80 n3=1 |\ sfgrey pclip=99 color=j title='snapshot at t=0.4s' |\ sfpen
- View the data recorded at receiver:
<Fdat.rsf sfwindow |\ sfgraph title='Data recorded at receiver' unit2= label2=amplitude |\ sfpen </bash>
Attention: time steps that are too large can result in numerical instability.
sfsrmig3
| 3-D S/R migration with extended SSF | |||
|---|---|---|---|
| sfsrmig3 slo=Fs_s.rsf sls=Fs_r.rsf < Fw_s.rsf rwf=Fw_r.rsf > Fi.rsf cig=Fc.rsf ompchunk=1 ompnth=0 verb=y eps=0.01 twoway=n nrmax=1 dtmax=0.004 pmx=0 pmy=0 tmx=0 tmy=0 vpvs=1. hsym=n nht=1 oht=0 dht=0.1 nht=1 oht=0 dht=0.1 hsym=n nhh=1 ohh=0 dhh=0.1 nha=180 oha=0 dha=2.0 nhb=180 ohb=0 dhb=2.0 itype= | |||
| file | cig= | auxiliary output file name | |
| float | dha=2.0 | ||
| float | dhb=2.0 | ||
| float | dhh=0.1 | ||
| float | dht=0.1 | ||
| float | dtmax=0.004 | max time error | |
| float | eps=0.01 | stability parameter | |
| bool | hsym=n | [y/n] | |
| string | itype= | imaging condition type
| |
| int | nha=180 | ||
| int | nhb=180 | ||
| int | nhh=1 | ||
| int | nht=1 | ||
| int | nrmax=1 | max number of refs | |
| float | oha=0 | ||
| float | ohb=0 | ||
| float | ohh=0 | ||
| float | oht=0 | ||
| int | ompchunk=1 | OpenMP data chunk size | |
| int | ompnth=0 | OpenMP available threads | |
| int | pmx=0 | padding on x | |
| int | pmy=0 | padding on y | |
| file | rwf= | auxiliary input file name | |
| file | slo= | auxiliary input file name | |
| string | sls= | auxiliary input file name | |
| int | tmx=0 | taper on x | |
| int | tmy=0 | taper on y | |
| bool | twoway=n | [y/n] | two-way traveltime |
| bool | verb=y | [y/n] | verbosity flag |
| float | vpvs=1. | Vp/Vs ratio | |
This program performs 3-D and 2-D shot-record (a.k.a. shot-profile) migration with an extended Split-Step Fourier (SSF) extrapolator with multiple reference velocities (hence "extended"). It takes as input a shot wavefield (stdin), receiver wavefield (rwf=) and slowness model (slo=). Outputs are an image (stdout) and a cube of Common Image Gathers (cig=). An important parameter is nrmax, the number of reference velocities. Its default value is 1, but for reasonable results it should be 5 or so. It is also good to specify nonzero taper values (tmx and, for 3-D, tmy as well). The values of padding parameters pmx and pmy are split in two by the program, i.e. if your data x axis is 501-points long, specify pmx=11 to get a value of 512 that will result in fast Fourier Transforms.
The program will also migrate converted-wave data if a file with the S-wave slowness model (sls=) is provided.
The vpvs parameter is only used when itype=h. Do not specify a vpvs value unless you know really well what you are doing.
Usage example
The commands below, slightly modified from RSFSRC/book/data/sigsbee/ptest, show how to prepare the Sigsbee 2A data and velocity for migration.
Convert input data (shots) from SEG-Y to RSF: <bash> sfsegyread tape=sigsbee2a_nfs.segy tfile=tdata.rsf hfile=/dev/null bfile=/dev/null > ddata.rsf </bash> Convert trace headers to float (required by sfheadermath): <bash> < tdata.rsf sfdd type=float > trchdr.rsf </bash> Shot positions: <bash> < trchdr.rsf sfheadermath output="fldr + 10925/150" | sfwindow squeeze=y > tsi.rsf </bash> Extract offset positions from the trace header files, eliminate length-1 axis, scale, create a header for binning (required by sfintbin): <bash> < trchdr.rsf sfheadermath output="offset" |\ sfwindow squeeze=y |\ sfmath output="input/75" |\ sfcat axis=2 space=n tsi.rsf |\ sftransp |\ sfdd type=int > tos.rsf </bash> Binning and muting: <bash> < ddata.rsf sfintbin head=tos.rsf xkey=0 ykey=1 |\ sfput label1=Time unit1=s d2=0.075 o2=0.0 label2=hx d3=0.150 o3=10.925 label3=sx |\ sfmutter half=false t0=1.0 v0=6.0 |\ sfput d2=0.02286 o2=0 unit2=km d3=0.04572 o3=3.32994 unit3=km > shots.rsf </bash> Keeping only 20 shots so that this 1-node job will not take forever, FFT-ing, decimating frequency slices (same as shortening the time axis), and creating y and hy axes of length 1: <bash> < shots.rsf sfwindow n3=20 f3=10 j3=20 |\ sffft1 |\ sfwindow n1=200 min1=1 j1=3 |\ sfspray axis=3 n=1 o=0 d=1 label=hy |\ sfspray axis=5 n=1 o=0 d=1 label=sy > rfft.rsf </bash> The dimensions of the cube thus created are:
$ sfin rfft.rsf trail=n
rfft.rsf:
in="/var/tmp/rfft.rsf@"
esize=8 type=complex form=native
n1=200 d1=0.25 o1=1 label1="Frequency" unit1="Hz"
n2=348 d2=0.02286 o2=0 label2="hx" unit2="km"
n3=1 d3=1 o3=0 label3="hy" unit3="km"
n4=20 d4=0.9144 o4=3.78714 label4="sx" unit4="km"
1392000 elements 11136000 bytes
Create the source wavelet (limited to the same frequency band as the data) and Fourier transform it: <bash> sfspike k1=1 n1=1500 d1=0.008 |\ sfbandpass flo=15 fhi=25 |\ sffft1 |\ sfwindow n1=200 min1=1 j1=3 |\ sfput label1=freq > sfft.rsf </bash> This creates a frequency-domain wavelet:
$ sfin sfft.rsf
sfft.rsf:
in="/var/tmp/sfft.rsf@"
esize=8 type=complex form=native
n1=200 d1=0.25 o1=1 label1="freq" unit1="Hz"
200 elements 1600 bytes
Create "synched" source and receiver wavefields with srsyn from wavelet and data frequency slices. Basically both the receiver and shot frequency slices are "placed" at the right location and padded with zeros up to the dimension of the x axis specified below. <bash> < rfft.rsf sfsrsyn nx=1067 dx=0.02286 ox=3.05562 wav=sfft.rsf swf=swav.rsf > rwav.rsf </bash> This creates frequency slices ready for migration for both source and receiver, only axis 1 (frequency) must become axis 3, for both datasets: <bash> < swav.rsf sftransp plane=12 | sftransp plane=23 > stra.rsf </bash> <bash> < rwav.rsf sftransp plane=12 | sftransp plane=23 > rtra.rsf </bash> This creates a surface receiver wavefield ready for input to migration. Axis 4 is shot number. The values of axis 4 are arbitrary because each shot has been padded with zeros so that it covers the entire velocity model. Therefore the aperture of the downward continuation for each shot will be as large as the survey.
sfin trail=n rtra.rsf
rtra.rsf:
in="/var/tmp/rtra.rsf@"
esize=8 type=complex form=native
n1=1067 d1=0.02286 o1=3.05562 label1="x" unit1="km"
n2=1 d2=1 o2=0 label2="y" unit2="km"
n3=200 d3=0.25 o3=1 label3="w" unit3="Hz"
n4=20 d4=1 o4=0 label4="e" unit4="km"
4268000 elements 34144000 bytes
Convert the velocity model from SEG-Y to RSF, decimate, convert from feet to km, transpose, convert to slowness and insert an additional axis: <bash> sfsegyread tape=sigsbee2a_migvel.sgy tfile=/dev/null hfile=/dev/null bfile=/dev/null |\ sfput o1=0 d1=0.00762 label1=z unit1=km o2=3.05562 d2=0.01143 label2=x unit2=km |\ sfwindow j1=4 j2=2 |\ sfscale rscale=0.0003048 |\ sftransp |\ sfmath output="1/input" |\ sfspray axis=2 n=1 d=1 o=0 |\ sfput label2=y > slow.rsf </bash> This creates a slowness file ready for input to migration, with an x axis identical to the x axis of the wavefield files:
$ sfin slow.rsf
slow.rsf:
in="/var/tmp/slow.rsf@"
esize=4 type=float form=native
n1=1067 d1=0.02286 o1=3.05562 label1="x" unit1="km"
n2=1 d2=1 o2=0 label2="y" unit2="km"
n3=301 d3=0.03048 o3=0 label3="z" unit3="km"
321167 elements 1284668 bytes
Finally, the migration command (for a 4-processor machine, hence the ompnth value). We choose not to compute any image gathers (itype=o), but due to the construction of the program we still have to explicitly assign the cig tag, or else a RSF file with the name of the tag and no rsf extension will be created: <bash> < stra.rsf sfsrmig3 nrmax=20 dtmax=5e-05 eps=0.01 verb=y ompnth=4 \ tmx=16 rwf=rtra.rsf slo=slow.rsf itype=o cig=/dev/null > img.rsf </bash> The migration of 20 shots takes approximately 3 hours on a 4-processor machine (1 shot=9 minutes). Without the frequency slice decimation by a factor of 3 and the depth axis decimation by a factor of 4, it would have taken twelve times as much. The resulting image has a y axis of length 1:
$ sfin img.rsf trail=n
img.rsf:
in="/var/tmp/img.rsf@"
esize=4 type=float form=native
n1=1067 d1=0.02286 o1=3.05562 label1="x" unit1="km"
n2=1 d2=1 o2=0 label2="y" unit2="km"
n3=301 d3=0.03048 o3=0 label3="z" unit3="km"
321167 elements 1284668 bytes
To properly visualize the image, we need to eliminate the axis of length 1, then transpose the x and z axes to their natural position: <bash> <img.rsf sfwindow squeeze=y | sftransp | sfgrey > img.vpl </bash>
References
- ↑ Claerbout, J., 1998, Multidimensional recursive filters via a helix: Geophysics, 63, 1532--1541.
- ↑ Claerbout, J., 1998, Multidimensional recursive filters via a helix: Geophysics, 63, 1532--1541.
- ↑ Barry, K.M., Cavers, D.A., and Kneale, C.W. 1975. Recommended standards for digital tape formats. Geophysics, 40, no. 02, 344–352.
- ↑ Norris, M.W., Faichney, A.K., Eds. 2001. SEG Y rev1 Data Exchange format. Society of Exploration Geophysicists, Tulsa, OK, 45 pp.






![{\displaystyle {\frac {1}{n-1}}\,\left[\sum \limits _{i=0}^{n}d_{i}^{2}-{\frac {1}{n}}\left(\sum \limits _{i=0}^{n}d_{i}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c6e744187777d584f3b3aa9e264f8274c8dd450)