A new paper is added to the collection of reproducible documents: Velocity analysis of simultaneous-source data using high-resolution semblance – coping with the strong noise


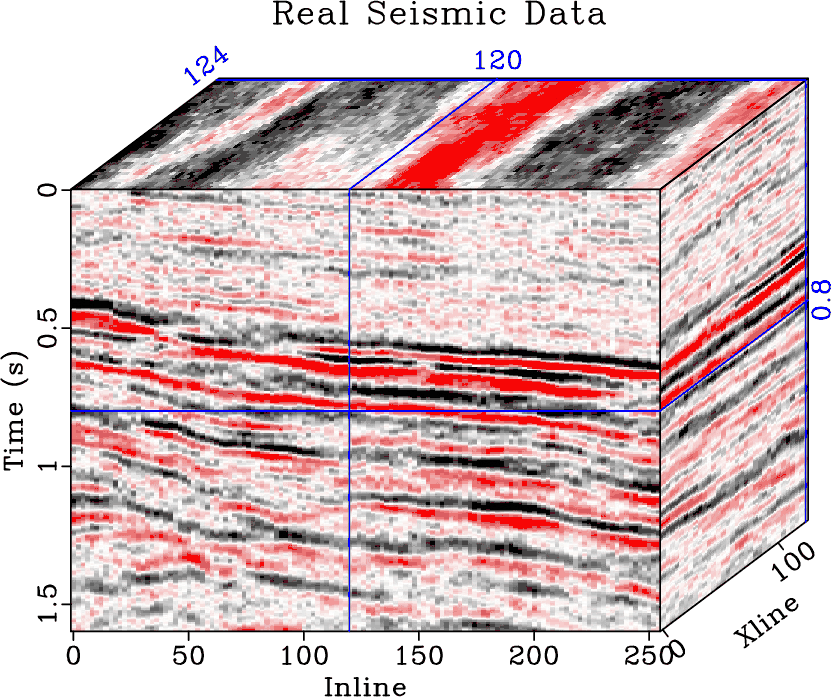
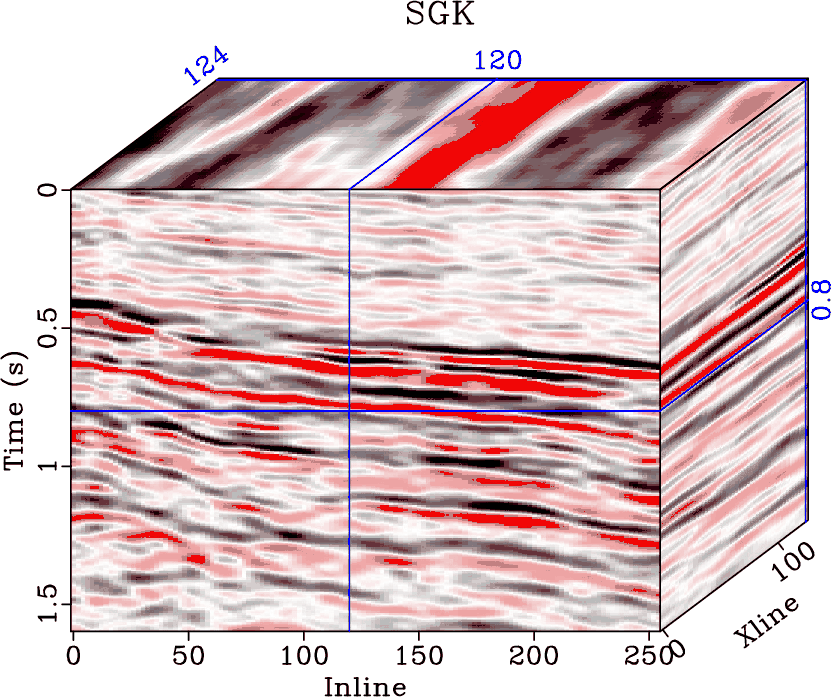
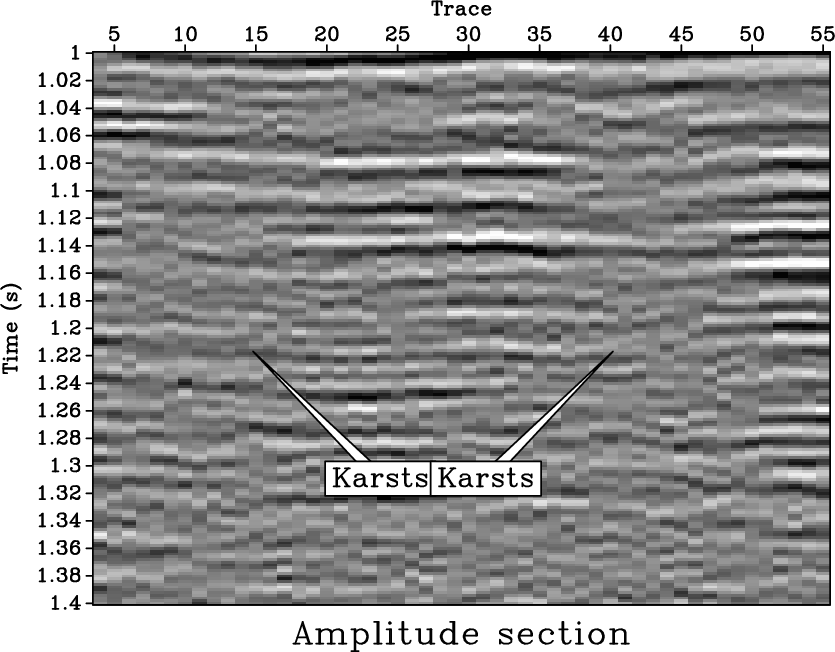
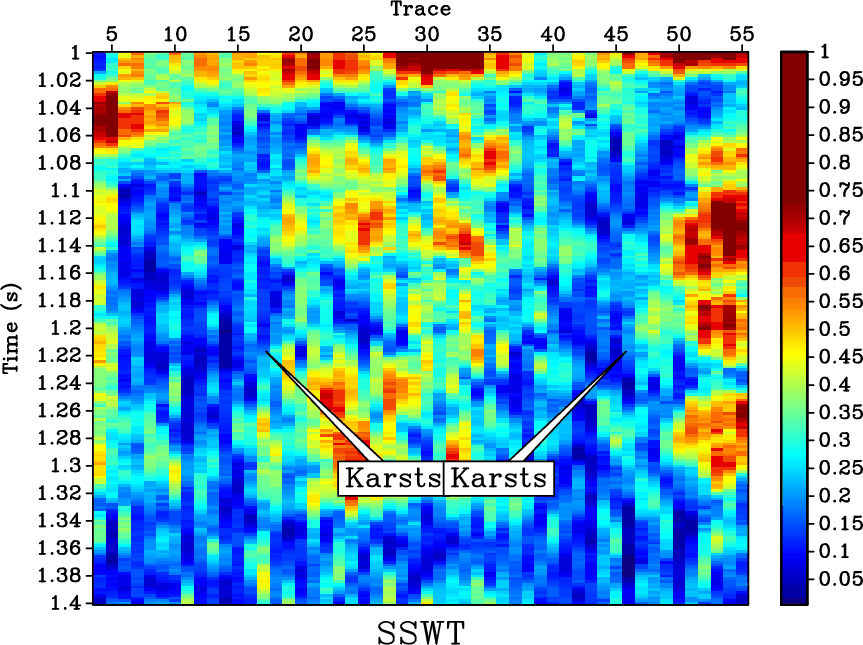
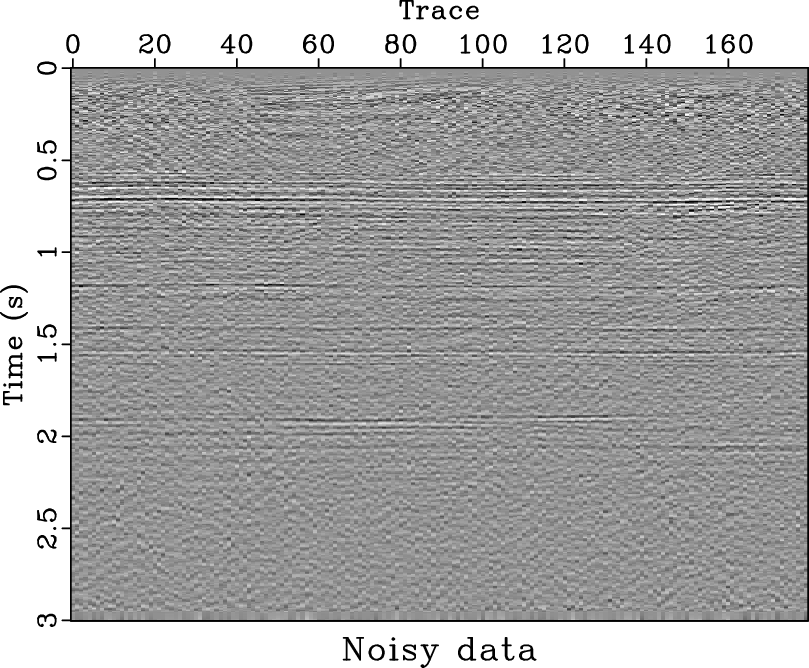
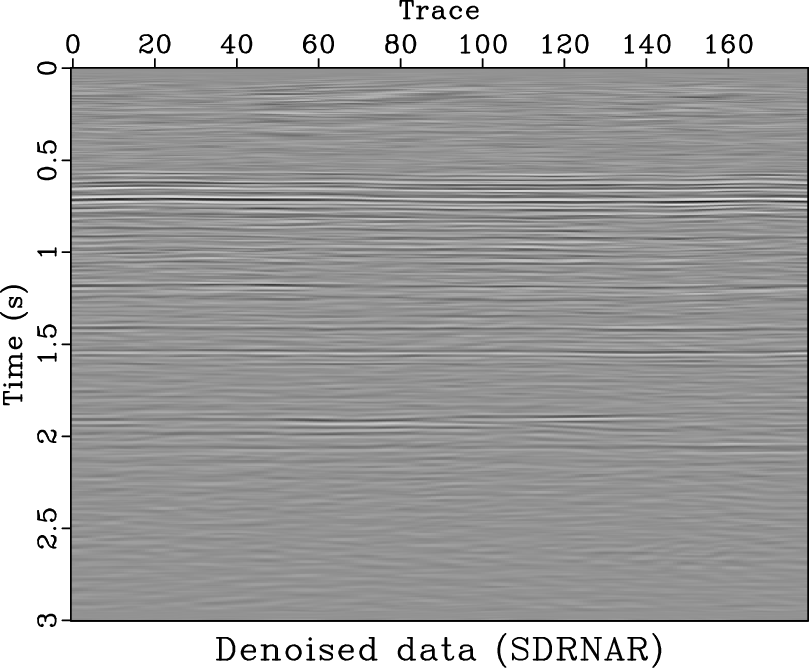
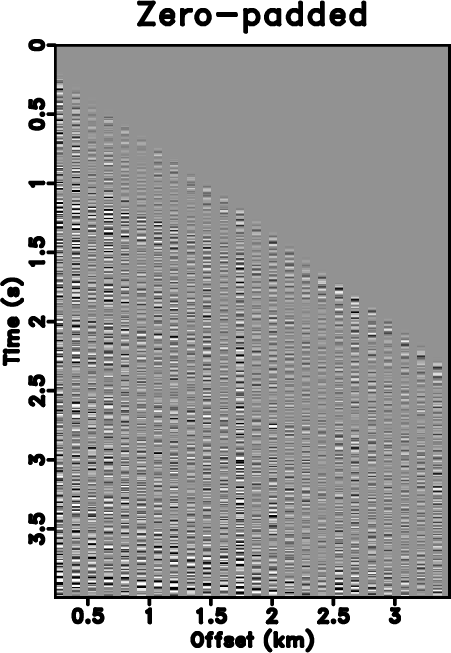
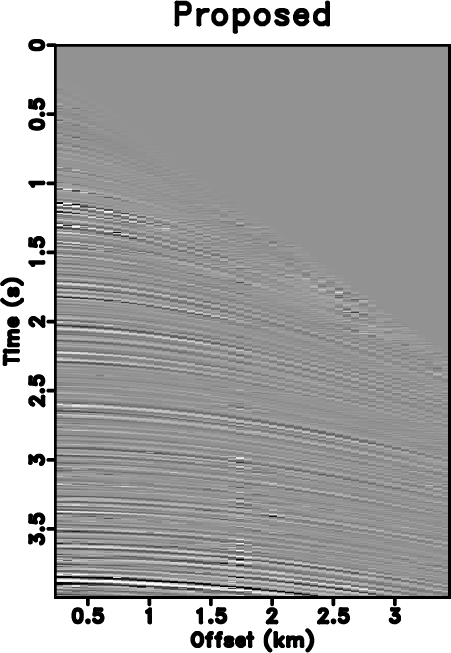
Direct imaging of simultaneous-source (or blended) data, without the need of deblending, requires a precise subsurface velocity model. In this paper, we focus on the velocity analysis of simultaneous-source data using the NMO-based velocity picking approach. We demonstrate that it is possible to obtain a precise velocity model directly from the blended data in the common-midpoint (CMP) domain. The similarity-weighted semblance can help us obtain much better velocity spectrum with higher resolution and higher reliability compared with the traditional semblance. The similarity-weighted semblance enforces an inherent noise attenuation solely in the semblance calculation stage, thus is not sensitive to the intense interference. We use both simulated synthetic and field data examples to demonstrate the performance of the similarity-weighted semblance in obtaining reliable subsurface velocity model for direct migration of simultaneous-source data. The migrated image of blended field data using prestack kirchhoff time migration (PSKTM) approach based on the picked velocity from the similarity-weighted semblance is very close to the migrated image of unblended data.