A new paper is added to the collection of reproducible documents: A variational approach for picking optimal surfaces from semblance-like panels

We propose and demonstrate a variational method for determining optimal velocity fields from semblance-like volumes using continuation. The proposed approach finds a minimal-cost surface through a volume, which often corresponds to a velocity field within a semblance scan. This allows picked velocity fields to incorporate information from gathers that are spatially near the midpoint in question. The minimization process amounts to solving a nonlinear elliptic partial differential equation, which is accomplished by changing the elliptic problem to a parabolic one and solving it iteratively until it converges to a critical point which minimizes the cost functional. The continuation approach operates by using a variational framework to iteratively minimize the cost of a velocity surface through successively less-smoothed semblance scans. The method works because a global minimum for the velocity cost functional can only exist when the semblance scan varies smoothly in space and convexly in the parameter being scanned. Using a discretization of the functional with a limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm we illustrate how the continuation approach is able to avoid local minima that would typically capture the iterative solution of an optimal velocity field determined without continuation. Incorporating continuation enables us to find a lower cost final model which is used for seismic processing of a field data set from the Viking Graben. We then utilize a field data set from the Gulf of Mexico to show how the final velocity model determined by the method employing continuation is largely independent of the starting velocity model, producing something resembling a global minimum. Finally, we illustrate the versatility of the variational picking approach by demonstrating how it may be used for automatic interpretation of a seismic horizon from the Heidrun Field.

A new paper is added to the collection of reproducible documents: Wave-equation time migration

Time migration, as opposed to depth migration, suffers from two well-known shortcomings: (1) approximate equations are used for computing Green’s functions inside the imaging operator; (2) in case of lateral velocity variations, the transformation between the image ray coordinates and the Cartesian coordinates is undefined in places where the image rays cross. We show that the first limitation can be removed entirely by formulating time migration through wave propagation in image-ray coordinates. The proposed approach constructs a time-migrated image without relying on any kind of traveltime approximation by formulating an appropriate geometrically accurate acoustic wave equation in the time-migration domain. The advantage of this approach is that the propagation velocity in image-ray coordinates does not require expensive model building and can be approximated by quantities that are estimated in conventional time-domain processing. Synthetic and field data examples demonstrate the effectiveness of the proposed approach and show that the proposed imaging workflow leads to a significant uplift in terms of image quality and can bridge the gap between time and depth migrations. The image obtained by the proposed algorithm is correctly focused and mapped to depth coordinates it is comparable to the image obtained by depth migration.

A new paper is added to the collection of reproducible documents: A probabilistic approach to seismic diffraction imaging

We propose and demonstrate a probabilistic method for imaging seismic diffractions based on path-integral imaging. Our approach utilizes oriented velocity continuation to produce a set of slope-decomposed diffraction images over a range of plausible migration velocities. Utilizing the assumption that each partial image in slope is independent enables us to construct an object resembling a probability field from the slope-decomposed images. That field may be used to create weights for each partial image in velocity corresponding to the likelihood of a correctly migrated diffraction occurring at a location within the seismic image for that migration velocity. Stacking these weighted partial images over velocity provides us with a path-integral seismic diffraction image created using probability weights. We illustrate the principles of the method on a simple toy model, show its robustness to noise on a synthetic, and apply it to a 2D field dataset from the Nankai Trough. We find that using the proposed approach creates diffraction images that enhance diffraction signal while suppressing noise, migration artifacts, remnant reflections, and other portions of the wavefield not corresponding to seismic diffraction relative to previously developed diffraction imaging methods, while simultaneously outputting the most likely migration velocity. The method is intended to be used on data which has already had much of the reflection energy removed using a method like plane-wave destruction. Although it suppresses residual reflection energy successfully, this suppression is less effective in the presence of strong reflections typically encountered in complete field data. The approach outlined in this paper is complimentary to existing data domain methods for diffraction extraction, and the probabilistic diffraction images it generates can supplement existing reflection and diffraction imaging methods by highlighting features that have a high likelihood of being diffractions and accentuating the geologically interesting objects in the subsurface that cause those features.

A new paper is added to the collection of reproducible documents: Noniterative f-x-y streaming prediction filtering for random noise attenuation on seismic data

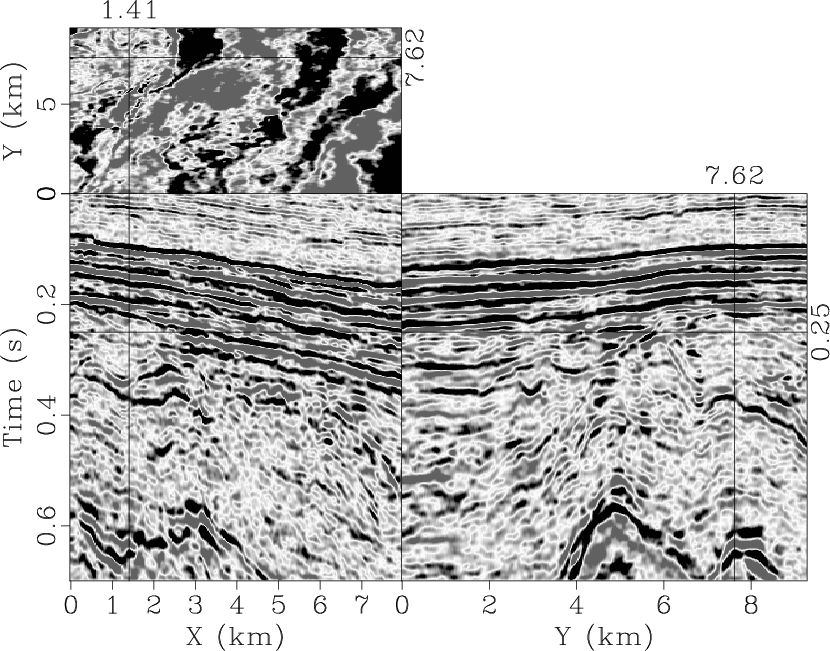
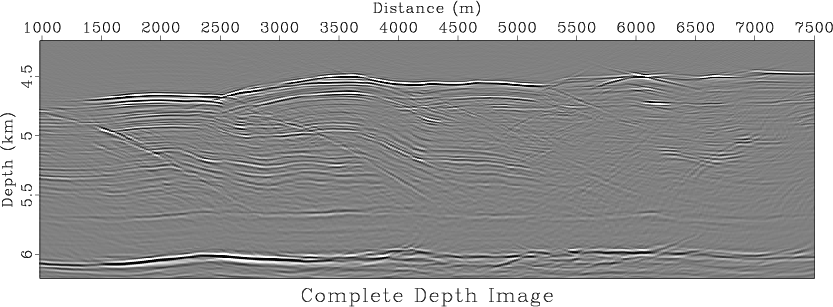
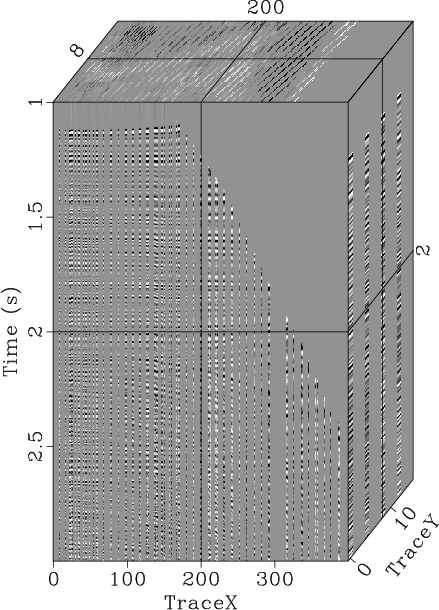
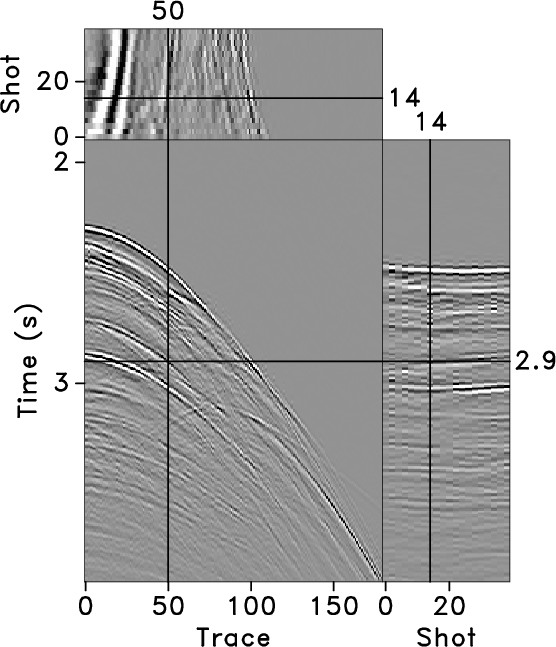
Random noise is unavoidable in seismic exploration, especially under complex-surface conditions and in deep-exploration environments. The current problems in random noise attenuation include preserving the nonstationary characteristics of the signal and reducing computational cost of broadband, wide-azimuth, and high-density data acquisition. To obtain high-quality images, traditional prediction filters (PFs) have proved effective for random noise attenuation, but these methods typically assume that the signal is stationary. Most nonstationary PFs use an iterative strategy to calculate the coefficients, which leads to high computational costs. In this study, we extended the streaming prediction theory to the frequency domain and proposed the f-x-y streaming prediction filter (SPF) to attenuate random noise. Instead of using the iterative optimization algorithm, we formulated a constraint least-squares problem to calculate the SPF and derived an analytical solution to this problem. The multi-dimensional streaming constraints are used to increase the accuracy of the SPF. We also modified the recursive algorithm to update the SPF with the snaky processing path, which takes full advantage of the streaming structure to improve the effectiveness of the SPF in high dimensions. In comparison with 2D f-x SPF and 3D f-x-y regularized nonstationary autoregression (RNA), we tested the practicality of the proposed method in attenuating random noise. Numerical experiments show that the 3D f-x-y SPF is suitable for large-scale seismic data with the advantages of low computational cost, reasonable nonstationary signal protection, and effective random noise attenuation.

A new paper is added to the collection of reproducible documents: Seismic data interpolation using streaming prediction filter in the frequency domain

Surface conditions and economic factors restrict field geometries, so seismic data acquisition typically obtains field data with irregular spatial distribution, which can adversely affect the subsequent data processing and interpretation. Therefore, data interpolation techniques are used to convert field data into regularly distributed data and reconstruct the missing traces. Recently, the mainstream methods have implemented iterative algorithms to solve data interpolation problems, which require substantial computational resources and restrict their application in high dimensions. In this study, we proposed the f-x and f-x-y streaming prediction filters (SPFs) to reconstruct missing seismic traces without iterations. According to the streaming computation framework, we directly derived an analytic solution to the overdetermined least-squares problem with local smoothness constraints for estimating SPFs in the frequency domain. We introduced different processing paths and filter forms to reduce the interference of missing traces, which can improve the accuracy of filter coefficients. Meanwhile, we utilized a two-step interpolation strategy to guarantee the effective interpolation of the irregularly missing traces. Numerical examples show that the proposed methods effectively recover the missing traces in seismic data when compared with the traditional Fourier Projection Onto Convex Sets (POCS) method. In particular, the frequency domain SPFs are suitable for high-dimensional seismic data interpolation with the advantages of low computational cost and reasonable nonstationary signal reconstruction.

A new paper is added to the collection of reproducible documents: Seismic data interpolation without iteration using t-x-y streaming prediction filter with varying smoothness

Although there is an increase in the amount of seismic data acquired with wide-azimuth geometry, it is difficult to achieve regular data distributions in spatial directions owing to limitations imposed by the surface environment and economic factor. To address this issue, interpolation is an economical solution. The current state of the art methods for seismic data interpolation are iterative methods. However, iterative methods tend to incur high computational cost which restricts their application in cases of large, high-dimensional datasets. Hence, we developed a two-step non-iterative method to interpolate nonstationary seismic data based on streaming prediction filters (SPFs) with varying smoothness in the time-space domain; and we extended these filters to two spatial dimensions. Streaming computation, which is the kernel of the method, directly calculates the coefficients of nonstationary SPF in the overdetermined equation with local smoothness constraints. In addition to the traditional streaming prediction-error filter (PEF), we proposed a similarity matrix to improve the constraint condition where the smoothness characteristics of the adjacent filter coefficient change with the varying data. We also designed non-causal in space filters for interpolation by using several neighboring traces around the target traces to predict the signal; this was performed to obtain more accurate interpolated results than those from the causal in space version. Compared with Fourier Projection onto a Convex Sets (POCS) interpolation method, the proposed method has the advantages such as fast computational speed and nonstationary event reconstruction. The application of the proposed method on synthetic and nonstationary field data showed that it can successfully interpolate high-dimensional data with low computational cost and reasonable accuracy even in the presence of aliased and conflicting events.

A new paper is added to the collection of reproducible documents: Nonstationary pattern-based signal-noise separation using adaptive prediction-error filter

Complex field conditions always create different interferences during seismic data acquisition, and there exist several types of noise in the recorded data, which affect the subsequent data processing and interpretation. To separate an effective signal from the noisy data, we adopted a pattern-based method with a two-step strategy, which involves two adaptive prediction-error filters (APEFs) corresponding to a nonstationary data pattern and noise pattern. By introducing shaping regularization, we first constructed a least-squares problem to estimate the filter coefficients of the APEF. Then, we solved another constrained least-square problem corresponding to the pattern-based signal-noise separation, and different pattern operators are adopted to characterize random noise and ground-roll noise. In comparison with traditional denoising methods, such as FXDECON, curvelet transform and local time-frequency (LTF) decomposition, we examined the ability of the proposed method by removing seismic random noise and ground-roll noise in several examples. Synthetic models and field data demonstrate the validity of the strategy for separating nonstationary signal and noise with different patterns.

A new paper is added to the collection of reproducible documents: Automatic channel detection using deep learning

We propose a method based on an encoder-decoder convolutional neural network for automatic channel detection in 3D seismic volumes. We use two architectures borrowed from computer vision which are SegNet for image segmentation together with Bayesian SegNet for uncertainty measurement. We train the network on 3D synthetic volumes and then apply it to field data. We test the proposed approach on a 3D field dataset from the Browse Basin, offshore Australia and a 3D Parihaka seismic data in New Zealand. Applying the weights estimated from training on 3D synthetic volumes to a 3D field dataset accurately identifies channel geobodies without the need for any human interpretation on seismic attributes. Our proposed method also produces uncertainty volumes to quantify the trustiness of detection model.