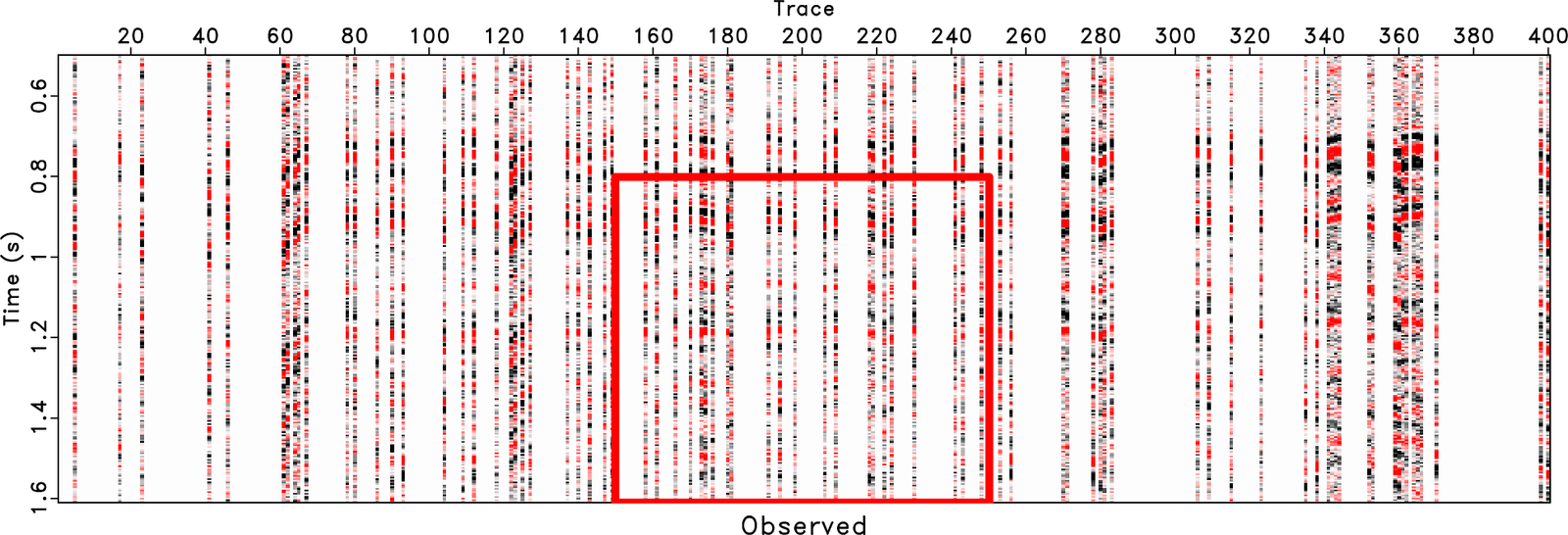
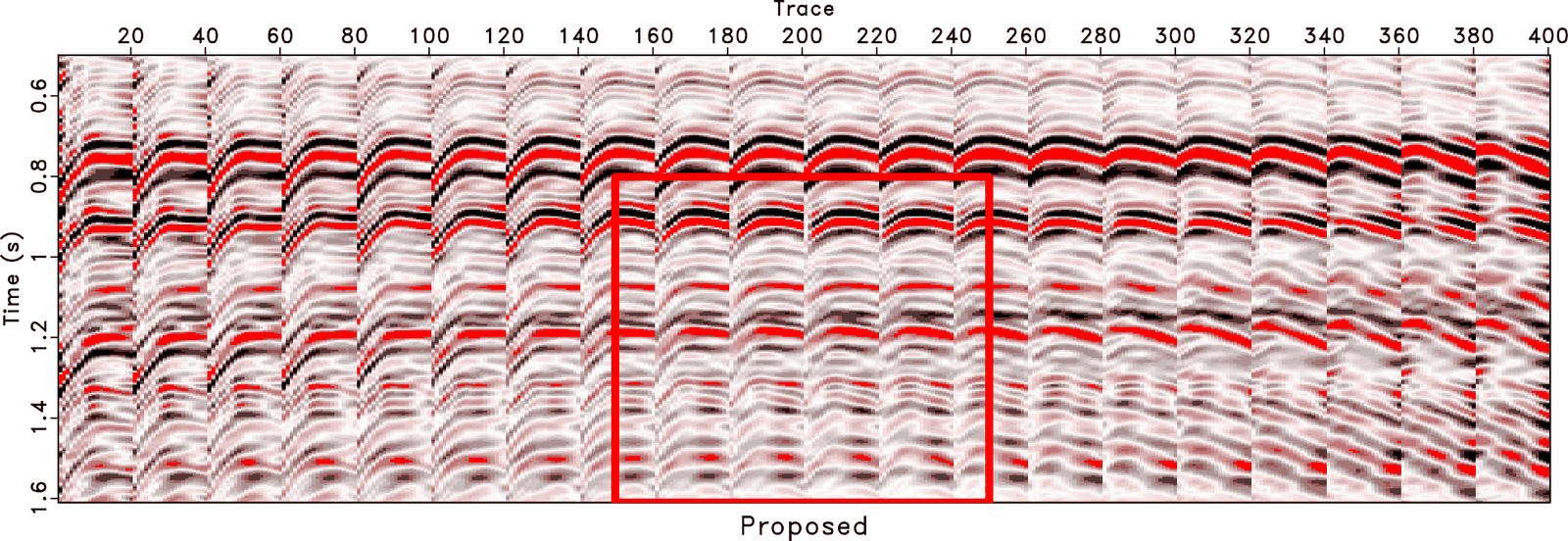
A new paper is added to the collection of reproducible documents: Seismic signal enhancement based on the lowrank methods

Based on the fact that the Hankel matrix constructed by noise-free seismic data is lowrank (LR), LR approximation (or rank-reduction) methods have been widely used for removing noise from seismic data. Due to the linear-event assumption of the traditional LR approximation method, it is difficult to define a rank that optimally separates the data subspace into signal and noise subspaces. For preserving the most useful signal energy, a relatively large rank threshold is often chosen, which inevitably leaves residual noise. To reduce the energy of residual noise, we propose an optimally damped rank-reduction method. The optimal damping is applied via two steps. In the first step, a set of optimal damping weights is derived. In the second step, we derive an optimal singular-value damping operator. We review several traditional lowrank methods and compare their performance with the new one. We also compare these lowrank methods with two sparsity-promoting transform methods. Examples demonstrate that the proposed optimally damped rank-reduction method could get significantly cleaner denoised images compared with the state-of-the-art methods.

A new paper is added to the collection of reproducible documents: Simultaneous denoising and reconstruction of 5D seismic data via damped rank-reduction method

The Cadzow rank-reduction method can be effectively utilized in simultaneously denoising and reconstructing 5D seismic data that depends on four spatial dimensions. The classic version of Cadzow rank-reduction method arranges the 4D spatial data into a level-four block Hankel/Toeplitz matrix and then applies truncated singular value decomposition (TSVD) for rank-reduction. When the observed data is extremely noisy, which is often the feature of real seismic data, traditional TSVD cannot be adequate for attenuating the noise and reconstructing the signals. The reconstructed data tends to contain a significant amount of residual noise using the traditional TSVD method, which can be explained by the fact that the reconstructed data space is a mixture of both signal subspace and noise subspace. In order to better decompose the block Hankel matrix into signal and noise components, we introduced a damping operator into the traditional TSVD formula, which we call the damped rank-reduction method. The damped rank-reduction method can obtain a perfect reconstruction performance even when the observed data has extremely low signal-to-noise ratio (SNR). The feasibility of the improved 5D seismic data reconstruction method was validated via both 5D synthetic and field data examples. We presented comprehensive analysis of the data examples and obtained valuable experience and guidelines in better utilizing the proposed method in practice. Since the proposed method is convenient to implement and can achieve immediate improvement, we suggest its wide application in the industry.