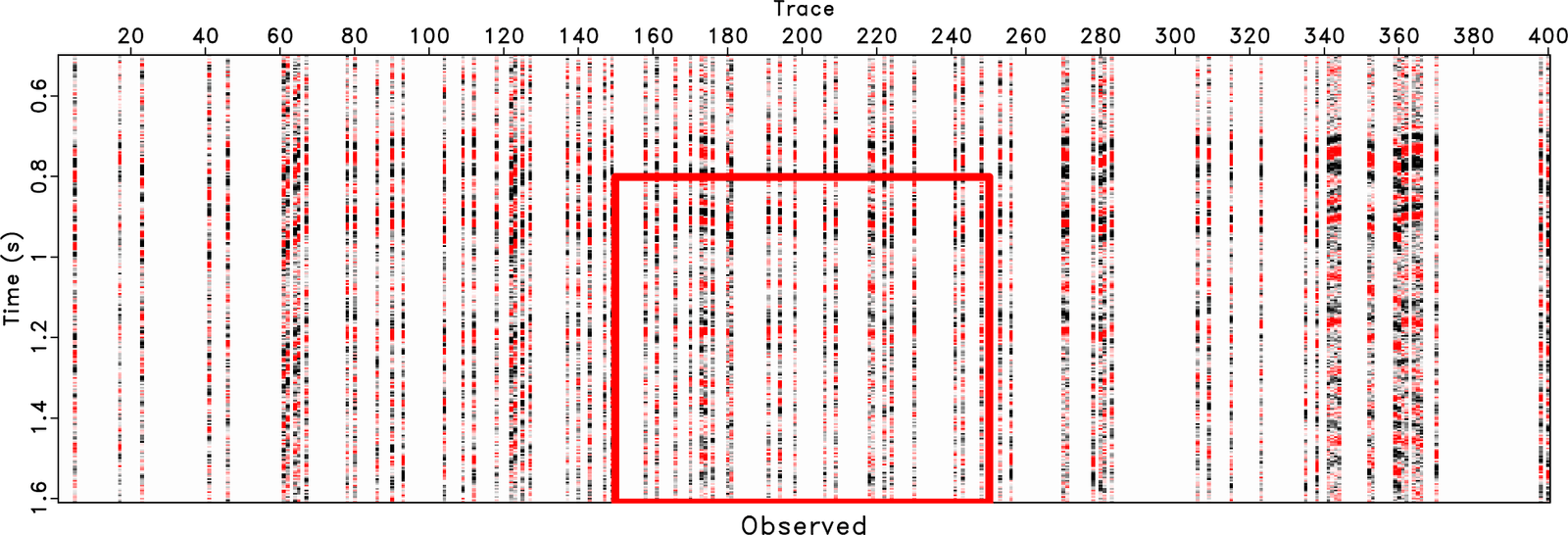
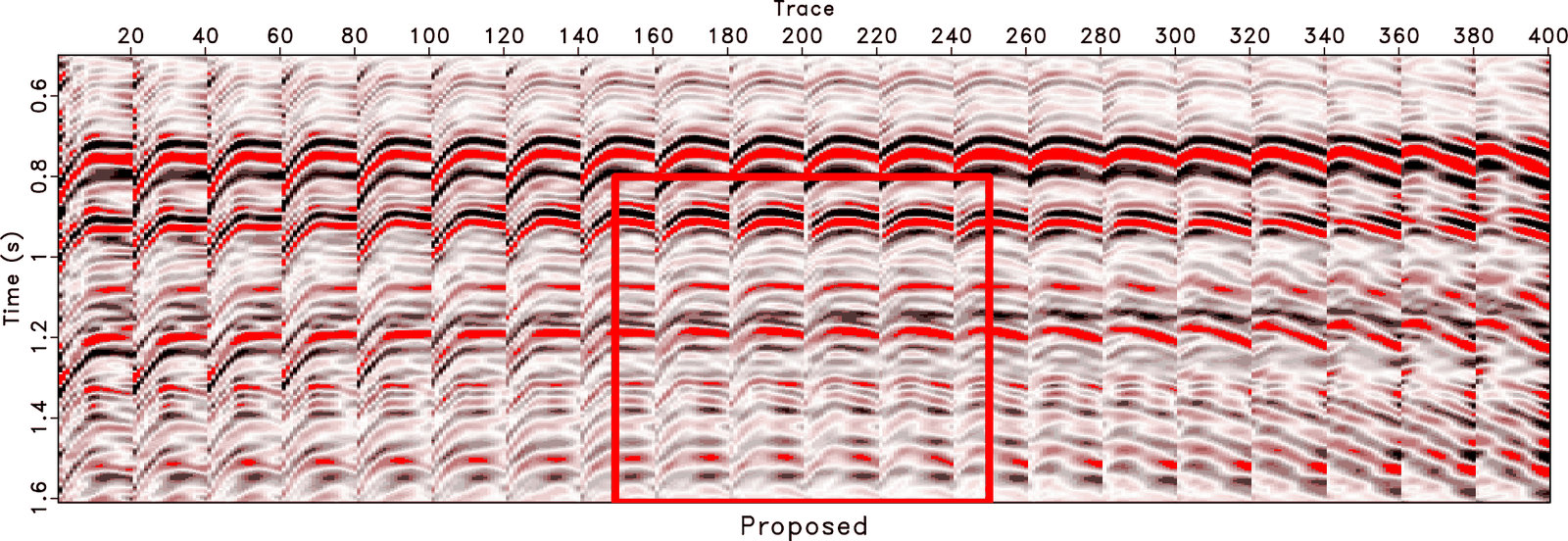
A new paper is added to the collection of reproducible documents: Full waveform inversion and joint migration inversion with an automatic directional total variation constraint

As full waveform inversion (FWI) is a non-unique and typically ill-posed inversion problem, it needs proper regularization to avoid cycle-skipping. To reduce the non-linearity of FWI, Joint Migration Inversion (JMI) is proposed as an alternative, explaining the reflection data with decoupled velocity and reflectivity parameters. However, the velocity update may also suffer from being trapped in local minima. To optimally include geologic information, we propose FWI/JMI with directional total variation as an L1-norm regularization on the velocity. We design the directional total variation operator based on the local dip field, instead of ignoring the local structural direction of the subsurface and only using horizontal- and vertical- gradients in the traditional TV. The local dip field is estimated using plane-wave destruction based on a raw reflectivity model, which is usually calculated from the initial velocity model. With two complex synthetic examples, based on the Marmousi model, we demonstrate that the proposed method is much more effective compared to both FWI/JMI without regularization and FWI/JMI with the conventional TV regularization. In the JMI-based example, we also show that L1 directional TV works better than L2 directional Laplacian smoothing. In addition, by comparing these two examples, it can be seen that the impact of regularization is larger for FWI than for JMI, because in JMI the velocity model only explains the propagation effects and, thereby, makes it less sensitive to the details in the velocity model.

A new paper is added to the collection of reproducible documents: Five-dimensional seismic data reconstruction using the optimally damped rank-reduction method

It is difficult to separate additive random noise from spatially coherent signal using a rank-reduction method that is based on the truncated singular value decomposition (TSVD) operation. This problem is due to the mixture of the signal and the noise subspaces after the TSVD operation. This drawback can be partially conquered using a damped rank reduction method, where the singular values corresponding to effective signals are adjusted via a carefully designed damping operator. The damping operator works most powerfully in the case of a small rank and a small damping factor. However, for complicated seismic data, e.g., multi-channel reflection seismic data containing highly curved events, the rank should be large enough to preserve the details in the data, which makes the damped rank reduction method less effective. In this paper, we develop an optimal damping strategy for adjusting the singular values when a large rank parameter is selected so that the estimated signal can best approximate the exact signal. We first weight the singular values using optimally calculated weights. The weights are theoretically derived by solving an optimization problem that minimizes the Frobenius-norm difference between the approximated signal components and the exact signal components. The damping operator is then derived based on the initial weighting operator to further reduce the residual noise after the optimal weighting. The resulted optimally damped rank reduction method is nearly an adaptive method, i.e., insensitive to the rank parameter. We demonstrate the performance of the proposed method on a group of synthetic and real five-dimensional seismic data.

A new paper is added to the collection of reproducible documents: Seismic signal enhancement based on the lowrank methods

Based on the fact that the Hankel matrix constructed by noise-free seismic data is lowrank (LR), LR approximation (or rank-reduction) methods have been widely used for removing noise from seismic data. Due to the linear-event assumption of the traditional LR approximation method, it is difficult to define a rank that optimally separates the data subspace into signal and noise subspaces. For preserving the most useful signal energy, a relatively large rank threshold is often chosen, which inevitably leaves residual noise. To reduce the energy of residual noise, we propose an optimally damped rank-reduction method. The optimal damping is applied via two steps. In the first step, a set of optimal damping weights is derived. In the second step, we derive an optimal singular-value damping operator. We review several traditional lowrank methods and compare their performance with the new one. We also compare these lowrank methods with two sparsity-promoting transform methods. Examples demonstrate that the proposed optimally damped rank-reduction method could get significantly cleaner denoised images compared with the state-of-the-art methods.

A new paper is added to the collection of reproducible documents: Simultaneous denoising and reconstruction of 5D seismic data via damped rank-reduction method

The Cadzow rank-reduction method can be effectively utilized in simultaneously denoising and reconstructing 5D seismic data that depends on four spatial dimensions. The classic version of Cadzow rank-reduction method arranges the 4D spatial data into a level-four block Hankel/Toeplitz matrix and then applies truncated singular value decomposition (TSVD) for rank-reduction. When the observed data is extremely noisy, which is often the feature of real seismic data, traditional TSVD cannot be adequate for attenuating the noise and reconstructing the signals. The reconstructed data tends to contain a significant amount of residual noise using the traditional TSVD method, which can be explained by the fact that the reconstructed data space is a mixture of both signal subspace and noise subspace. In order to better decompose the block Hankel matrix into signal and noise components, we introduced a damping operator into the traditional TSVD formula, which we call the damped rank-reduction method. The damped rank-reduction method can obtain a perfect reconstruction performance even when the observed data has extremely low signal-to-noise ratio (SNR). The feasibility of the improved 5D seismic data reconstruction method was validated via both 5D synthetic and field data examples. We presented comprehensive analysis of the data examples and obtained valuable experience and guidelines in better utilizing the proposed method in practice. Since the proposed method is convenient to implement and can achieve immediate improvement, we suggest its wide application in the industry.

A new paper is added to the collection of reproducible documents: Separation and imaging of seismic diffractions using a localized rank-reduction method with adaptively selected ranks

Seismic diffractions are some weak seismic events hidden within the more dominant reflection events in a seismic profile. Separating diffraction energy from the post-stack seismic profiles can help infer the subsurface discontinuities that generate the diffraction events. The separated seismic diffractions can be migrated with a traditional seismic imaging method or a specifically designed migration method to highlight the diffractors, i.e., the diffraction image. Traditional diffraction separation methods based on the the underlying plane-wave assumption are limited by either the inaccurate slope estimation or the plane-wave assumption of the PWD filter, and thus will cause reflection leakage into the separated diffraction profile. The leaked reflection energy will deteriorate the resolution of the subsequent diffraction imaging result. Here, we propose a new diffraction separation method based on a localized rank-reduction method. The localized rank-reduction method assumes the reflection events to be locally low-rank and the diffraction energy can be separated by a rank-reduction operation. Compared with the global rank-reduction method, the localized rank-reduction method is more constrained in selecting the rank and is free of separation artifacts. We use a carefully designed synthetic example to demonstrate that the localized rank-reduction method can help separate the diffraction energy from a post-stack seismic profile with both kinematically and dynamically accurate performance.