sfslpf estimates a non-stationary filter using shaping regularization.
The method is described in the reproducible paper Adaptive multiple subtraction using regularized nonstationary regressio
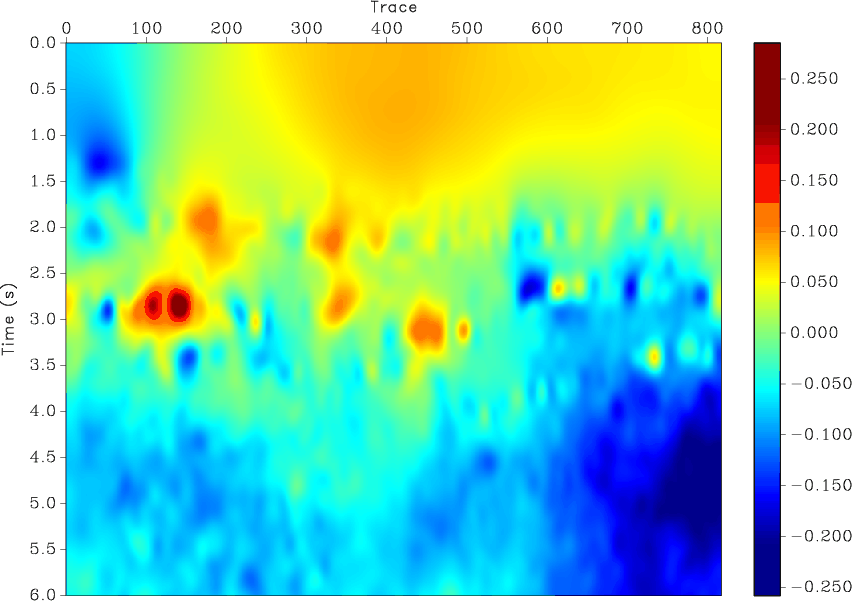
The following example from tccs/lpf/plut shows a common-offset section from the Pluto synthetic dataset before and after adaptive multiple subtraction with the help of sflpf.


Given target data $m(\mathbf{x})$ (specified with match= parameter) and a collection of fitting functions $s_k(\mathbf{x})$ (specified in the standard input), sflpf finds the fitting coefficients $b_k(\mathbf{x})$ by minimizing the error
$m(\mathbf{x}) – \displaystyle \sum_{k=1}^{N} b_k(\mathbf{x})\,s_k(\mathbf{x})$
while constraining the coefficients to be smooth. The smoothness is controlled by rect#= parameters, as in sfsmooth.
Shaping regularization is carried out iteratively, niter= controls the number of iterations.
The mean coefficient from the example above is shown in the figure below.
Optionally, a prediction-error filter can be applied to whiten the residual. The filter is specified with the help of pef= and lag= parameters, with a multidimensional helical filter specified as in sfhelicon.
The complex version of the same program is sfclpf.