A new paper is added to the collection of reproducible documents: Viscoacoustic modeling and imaging using low-rank approximation
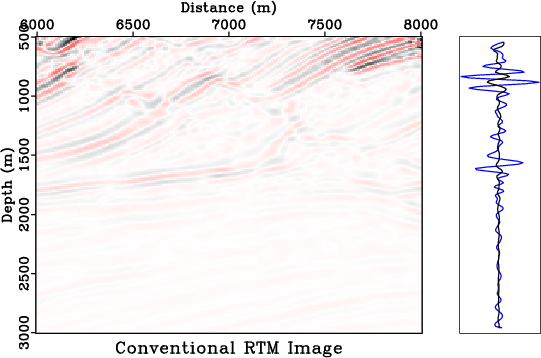
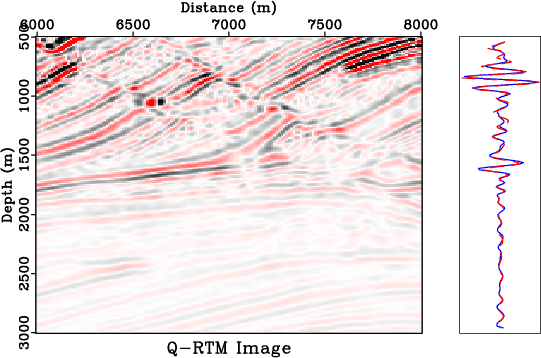
A constant-$Q$ wave equation involving fractional Laplacians was recently introduced for viscoacoustic modeling and imaging. This fractional wave equation has a convenient mixed-domain space-wavenumber formulation, which involves the fractional-Laplacian operators with a spatially varying power. We propose to apply low-rank approximation to the mixed-domain symbol, which enables a space-variable attenuation specified by the variable fractional power of the Laplacians. Using the proposed approximation scheme, we formulate the framework of the $Q$-compensated reverse-time migration ($Q$-RTM) for attenuation compensation. Numerical examples using synthetic data demonstrate the improved accuracy of using low-rank wave extrapolation with a constant-$Q$ fractional-Laplacian wave equation for seismic modeling and migration in attenuating media. Low-rank $Q$-RTM applied to viscoacoustic data is capable of producing images comparable in quality with those produced by conventional RTM from acoustic data.