In a seismic profile, the amplitude of time 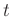 and space
and space 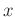 can be expressed as:
can be expressed as:
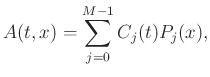 |
(1) |
where
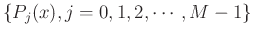 is a set of orthogonal polynomials and
is a set of orthogonal polynomials and  is the number of basis functions and
is the number of basis functions and
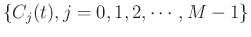 is a set of coefficients. The
is a set of coefficients. The  is a unit basis function that satisfies the condition:
is a unit basis function that satisfies the condition:
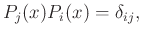 |
(2) |
where
 denotes the Kronecker delta. The spectrum defined by
denotes the Kronecker delta. The spectrum defined by 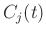 denotes the energy distribution of the
denotes the energy distribution of the  domain data in the orthogonal polynomials transform domain. Besides, the low-order coefficients represent the effective energy and the high-order coefficients represent the random noise energy. We provide a detailed introduction about how we construct the orthogonal polynomial basis function in Appendix A.
domain data in the orthogonal polynomials transform domain. Besides, the low-order coefficients represent the effective energy and the high-order coefficients represent the random noise energy. We provide a detailed introduction about how we construct the orthogonal polynomial basis function in Appendix A.
In a matrix-multiplication form, equation 1 can be expressed as the following equation
 |
(3) |
where
 is constructed from
is constructed from  ,
,
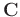 is constructed from
is constructed from 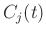 ,
,
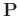 is constructed from
is constructed from  .
.
 is known and
is known and
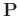 can be constructed using the way introduced in Appendix A. The unknown is
can be constructed using the way introduced in Appendix A. The unknown is
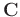 .
.
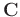 can be obtained by inverting the equation 3
can be obtained by inverting the equation 3
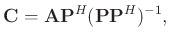 |
(4) |
where ![$[\cdot]^H$](img27.png) denotes matrix tranpose.
In this paper, we choose
denotes matrix tranpose.
In this paper, we choose 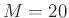 , which indicates that we select 20 orthogonal polynomial basis function to represent the seismic data. Hence, inverting equation
, which indicates that we select 20 orthogonal polynomial basis function to represent the seismic data. Hence, inverting equation
 is simply inverting a
is simply inverting a
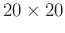 matrix and is computationally efficient.
matrix and is computationally efficient.
In the OPT method, we need to define the order of coefficients we want to preserve, the process of which corresponds to applying a mask operator to the orthogonal polynomial coefficients. Mask operator can be chosen to preserve low-order coefficients and reject high-order coefficients. It takes the following form:
 |
(5) |
where
 denotes the mask operator,
denotes the mask operator, 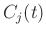 denotes the orthogonal polynomial coefficients at time
denotes the orthogonal polynomial coefficients at time 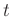 and order
and order 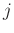 .
.
The coefficients after applying the mask operator 5 become
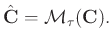 |
(6) |
The useful signals can be reconstructed by
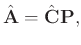 |
(7) |
where
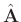 denotes the denoised data.
denotes the denoised data.
2020-03-27