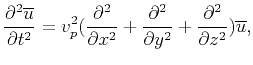|
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: Pseudo-pure-mode qP-wave equation in
Up: Pseudo-pure-mode qP-wave equation
Previous: Pseudo-pure-mode qP-wave equation
For a VTI medium, there are only five independent parameters: 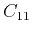 ,
,  ,
, 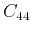 ,
, 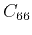 and
and 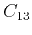 ,
with
,
with
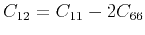 ,
,
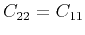 ,
,
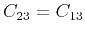 and
and
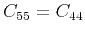 .
So we rewrite equation 18 as,
.
So we rewrite equation 18 as,
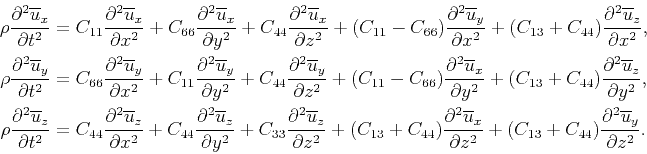 |
(19) |
Since a TI material has cylindrical symmetry in its elastic properties, it is safe to sum the first two equations
in equation 19 to yield a simplified form for wavefield modeling and RTM, namely
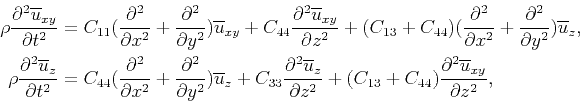 |
(20) |
where
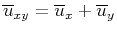 represents the sum of the two horizontal components.
Pure SH-waves horizontally polarize in the isotropic planes of VTI media
with the polarization given by
represents the sum of the two horizontal components.
Pure SH-waves horizontally polarize in the isotropic planes of VTI media
with the polarization given by
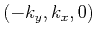 , which implies
, which implies
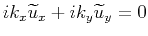 ,
i.e.,
,
i.e.,
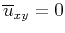 , for the SH-wave.
Therefore, the above partial summation (after the first-step projection) completes divergence operation and removes the SH-waves from
the three-component pseudo-pure-mode qP-wave fields.
As a result, there are no terms related to
, for the SH-wave.
Therefore, the above partial summation (after the first-step projection) completes divergence operation and removes the SH-waves from
the three-component pseudo-pure-mode qP-wave fields.
As a result, there are no terms related to 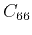 any more in equation 20.
Compared with original elastic wave equation, equation 20 further reduces the compuational
costs for 3D wavefield modeling and RTM for VTI media.
any more in equation 20.
Compared with original elastic wave equation, equation 20 further reduces the compuational
costs for 3D wavefield modeling and RTM for VTI media.
Applying the Thomsen notation (Thomsen, 1986),
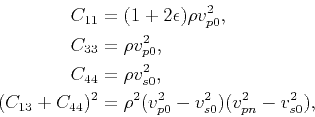 |
(21) |
the pseudo-pure-mode qP-wave equation can be expressed as,
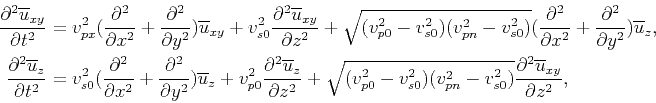 |
(22) |
where  and
and  represent the vertical velocities of qP- and qSV-waves,
represent the vertical velocities of qP- and qSV-waves,
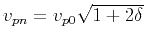 represents the interval
NMO velocity,
represents the interval
NMO velocity,
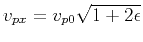 represents the horizontal velocity of qP-waves,
represents the horizontal velocity of qP-waves,
 and
and  are the other two Thomsen coefficients.
Unlike other coupled second-order systems derived from the dispersion relation
of VTI media (Zhou et al., 2006b), the wavefield components in
equations 20 and 22
have clear physical meaning and their summation automatically produces scalar wavefields dominant of qP-wave energy.
Equation 22 is also similar to a minimal coupled system (equation 30 in their paper)
demonstrated by Fowler
et al. (2010), except that it is now derived from a significant similarity transformation that helps to
enhance qP-waves and suppress qS-waves (after summing the transformed wavefield components).
This is undoubtedly useful for migration of conventional seismic data representing mainly qP-wave data.
are the other two Thomsen coefficients.
Unlike other coupled second-order systems derived from the dispersion relation
of VTI media (Zhou et al., 2006b), the wavefield components in
equations 20 and 22
have clear physical meaning and their summation automatically produces scalar wavefields dominant of qP-wave energy.
Equation 22 is also similar to a minimal coupled system (equation 30 in their paper)
demonstrated by Fowler
et al. (2010), except that it is now derived from a significant similarity transformation that helps to
enhance qP-waves and suppress qS-waves (after summing the transformed wavefield components).
This is undoubtedly useful for migration of conventional seismic data representing mainly qP-wave data.
We can also obtain a pseudo-acoustic coupled system by setting 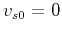 in equation 22, namely:
in equation 22, namely:
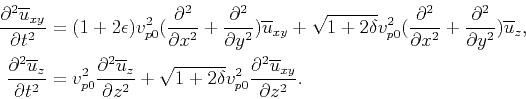 |
(23) |
The pseudo-acoustic approximation does not significantly
affect the kinematic signatures but may distort the reflection,
transmission and conversion coefficients (thus the amplitudes) of waves in elastic media.
If we further apply the isotropic assumption (seting 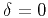 and
and
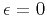 ) and sum the two equations in
equation 23, we get the familar constant-density acoustic wave equation:
) and sum the two equations in
equation 23, we get the familar constant-density acoustic wave equation:
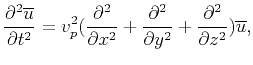 |
(24) |
where
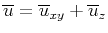 represents the acoustic pressure wavefield, and
represents the acoustic pressure wavefield, and 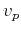 is
the propagation velocity of isotropic P-wave.
is
the propagation velocity of isotropic P-wave.
 |
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: Pseudo-pure-mode qP-wave equation in
Up: Pseudo-pure-mode qP-wave equation
Previous: Pseudo-pure-mode qP-wave equation
2014-06-24
![]() in equation 22, namely:
in equation 22, namely:
![]() and
and
![]() ) and sum the two equations in
equation 23, we get the familar constant-density acoustic wave equation:
) and sum the two equations in
equation 23, we get the familar constant-density acoustic wave equation: