|
|
|
|
Probabilistic moveout analysis by time warping |
Next: Monte Carlo inversion Up: Theory Previous: Time-warping workflow
 and
and  in a given acquisition coordinate frame as
in a given acquisition coordinate frame as 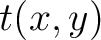 . The 3D generalized nonhyperboloidal moveout approximation (3D GMA) can be expressed as (Sripanich et al., 2017):
where
. The 3D generalized nonhyperboloidal moveout approximation (3D GMA) can be expressed as (Sripanich et al., 2017):
where
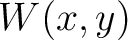 |
 |
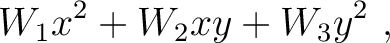 |
|
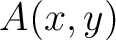 |
 |
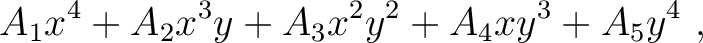 |
|
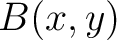 |
 |
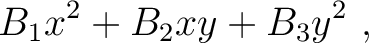 |
|
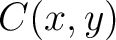 |
 |
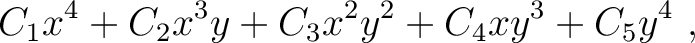 |
(5) |
 again denotes the reflection traveltime at zero offset. The total number of independent parameters in equation 4 is seventeen including
again denotes the reflection traveltime at zero offset. The total number of independent parameters in equation 4 is seventeen including  ,
,  ,
,  ,
,  , and
, and  . In the case of
. In the case of 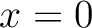 or
or 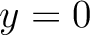 , equation 4 reduces to the generalized nonhyperbolic moveout approximation of Fomel and Stovas (2010). Sripanich et al. (2017) shows that the 3D GMA (equation 4) can predict reflection traveltimes in 3D homogeneous or complex horizontally layered anisotropic models with a nearly exact level of accuracy for all practical purposes.
, equation 4 reduces to the generalized nonhyperbolic moveout approximation of Fomel and Stovas (2010). Sripanich et al. (2017) shows that the 3D GMA (equation 4) can predict reflection traveltimes in 3D homogeneous or complex horizontally layered anisotropic models with a nearly exact level of accuracy for all practical purposes.
In equation 4, the parameters  ,
,  , and
, and  are defined with respect to the zero-offset ray, whereas
are defined with respect to the zero-offset ray, whereas  and
and  are obtained from finite-offset rays (Sripanich et al., 2017). With these definitions, the parameters
are obtained from finite-offset rays (Sripanich et al., 2017). With these definitions, the parameters  ,
,  , and
, and  are related to previously known time-processing parameters:
are related to previously known time-processing parameters:  simply denote the reciprocals of NMO velocities and govern the so-called NMO ellipse (Grechka and Tsvankin, 1998a).
simply denote the reciprocals of NMO velocities and govern the so-called NMO ellipse (Grechka and Tsvankin, 1998a).  represent the quartic coefficients that govern the nonhyperbolicity of reflection traveltimes. A common approach to simplify and relate the quartic coefficients (
represent the quartic coefficients that govern the nonhyperbolicity of reflection traveltimes. A common approach to simplify and relate the quartic coefficients ( ) to anisotropic parameters of the subsurface medium is done using the pseudoacoustic approximation, where
) to anisotropic parameters of the subsurface medium is done using the pseudoacoustic approximation, where  can then be expressed in terms of
can then be expressed in terms of 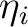 (Alkhalifah, 2003; Sripanich and Fomel, 2016; Alkhalifah and Tsvankin, 1995; Sripanich et al., 2017; Stovas, 2015). With regard to this study, we keep the
(Alkhalifah, 2003; Sripanich and Fomel, 2016; Alkhalifah and Tsvankin, 1995; Sripanich et al., 2017; Stovas, 2015). With regard to this study, we keep the  notation to maintain the generality of the proposed moveout inversion approach.
notation to maintain the generality of the proposed moveout inversion approach.
On the other hand, the  and
and  are designed to be dynamic and can vary with respect to different choices of finite-offset rays, which lead to better flexibility and accuracy of traveltime fitting. As a result, they cannot be directly related to medium parameters and one may expect that there are many possibilities of
are designed to be dynamic and can vary with respect to different choices of finite-offset rays, which lead to better flexibility and accuracy of traveltime fitting. As a result, they cannot be directly related to medium parameters and one may expect that there are many possibilities of  and
and  that can lead to equally good approximation accuracy. Therefore, we expect that the non-uniqueness of
that can lead to equally good approximation accuracy. Therefore, we expect that the non-uniqueness of  and
and  can lead also to the non-uniqueness in the final inverted models.
can lead also to the non-uniqueness in the final inverted models.