 |
 |
 |
 | Time-lapse image registration using the local similarity attribute |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Fomel & Jin: Time-lapse
Previous: Introduction
The correlation coefficient between two data sequences 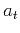 and
and 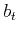 is defined as
is defined as
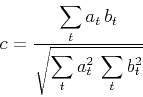 |
(1) |
and ranges between 1 (perfect correlation) and -1 (perfect correlation
of signals with different polarity). The definition of the local
similarity attribute (Fomel, 2007a) starts with the observation that
the squared correlation coefficient can be represented as the product
of two quantities 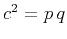 , where
, where
is the solution of the least-squares minimization problem
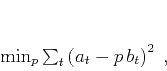 |
(2) |
and
is the solution of the least-squares minimization
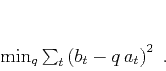 |
(3) |
Analogously, the local similarity 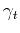 is a variable signal
defined as the product of two variable signals
is a variable signal
defined as the product of two variable signals 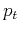 and
and 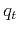 that
are the solutions of the regularized least-squares problems
that
are the solutions of the regularized least-squares problems
![$\displaystyle \min_{p_t}
\left(\sum\nolimits_t \left(a_t - p_t\,b_t\right)^2 + R\left[p_t\right]\right)\;,$](img12.png) |
|
|
(4) |
![$\displaystyle \min_{q_t}
\left(\sum\nolimits_t \left(b_t - q_t\,a_t\right)^2 + R\left[q_t\right]\right)\;,$](img13.png) |
|
|
(5) |
where 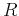 is a regularization operator designed to enforce a desired
behavior such as smoothness. Shaping regularization (Fomel, 2007b)
provides a particularly convenient method of enforcing smoothness in
iterative optimization schemes. If shaping regularization is applied
iteratively with Gaussian smoothing as a shaping operator, its first
iteration is equivalent to the fast local cross-correlation method of
Hale (2006). Further iterations introduce relative amplitude
normalization and compensate for amplitude effects on the local image
similarity. Choosing the amount of regularization (smoothness of the
shaping operator) affects the results. In practice, we start with
strong smoothing and decrease it when the results stop changing and
before they become unstable.
is a regularization operator designed to enforce a desired
behavior such as smoothness. Shaping regularization (Fomel, 2007b)
provides a particularly convenient method of enforcing smoothness in
iterative optimization schemes. If shaping regularization is applied
iteratively with Gaussian smoothing as a shaping operator, its first
iteration is equivalent to the fast local cross-correlation method of
Hale (2006). Further iterations introduce relative amplitude
normalization and compensate for amplitude effects on the local image
similarity. Choosing the amount of regularization (smoothness of the
shaping operator) affects the results. In practice, we start with
strong smoothing and decrease it when the results stop changing and
before they become unstable.
The application of local similarity to the time-lapse image
registration problem consists of squeezing and stretching the monitor
image with respect to the base image while computing the local
similarity attribute. Next, we pick the strongest similarity trend
from the attribute panel and apply the corresponding shift to the image.
In addition to its use for image registration, the estimated local
time shift is a useful attribute by itself. Time shift analysis has
been widely applied to infer reservoir compaction
(Hatchell and Bourne, 2005; Janssen et al., 2006; Tura et al., 2005; Rickett et al., 2007). Since the time shift has a
cumulative effect, it is helpful to compute the derivative of time
shift, which can relate the time shift change to the corresponding
reservoir layer. Rickett et al. (2007) define the derivative of time shift
as time strain and find it to be an
intuitive attribute for studying reservoir
compaction.
What is the exact physical meaning of the warping function 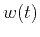 that
matches the monitor image
that
matches the monitor image 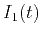 with the
base image
with the
base image 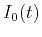 by applying the
transformation
by applying the
transformation ![$I_1[w(t)]$](img18.png) ? One can define the
base traveltime as an integral in depth, as follows:
? One can define the
base traveltime as an integral in depth, as follows:
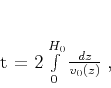 |
(6) |
where 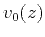 is the base velocity, and
is the base velocity, and 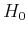 is the base depth. A similar event in the
monitor image appears at time
is the base depth. A similar event in the
monitor image appears at time
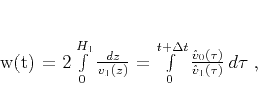 |
(7) |
where 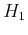 is the monitor depth,
is the monitor depth, 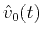 and
and 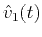 are seismic velocities as functions of time rather than depth, and
are seismic velocities as functions of time rather than depth, and
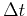 is the part of the time shift caused by the reflector
movement:
is the part of the time shift caused by the reflector
movement:
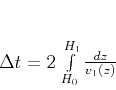 |
(8) |
In a situation where the change of 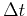 with
with 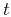 can be neglected,
a simple differentiation of the function
can be neglected,
a simple differentiation of the function
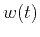 detected by the local similarity analysis provides an estimate
of the local ratio of the velocities:
detected by the local similarity analysis provides an estimate
of the local ratio of the velocities:
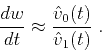 |
(9) |
If the registration is correct, the estimated velocity ratio outside
of the reservoir should be close to one. One can connect
the local velocity ratio to other physical attributes that are
related to changes in saturation, pore pressure, or compaction.
We demonstrate the proposed procedure in the next section using several
examples.
 |
 |
 |
 | Time-lapse image registration using the local similarity attribute |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Fomel & Jin: Time-lapse
Previous: Introduction
2013-07-26
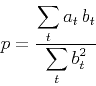
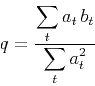
![]() that
matches the monitor image
that
matches the monitor image ![]() with the
base image
with the
base image ![]() by applying the
transformation
by applying the
transformation ![]() ? One can define the
base traveltime as an integral in depth, as follows:
? One can define the
base traveltime as an integral in depth, as follows:
![]() with
with ![]() can be neglected,
a simple differentiation of the function
can be neglected,
a simple differentiation of the function
![]() detected by the local similarity analysis provides an estimate
of the local ratio of the velocities:
detected by the local similarity analysis provides an estimate
of the local ratio of the velocities: