 |
 |
 |
 | Time-to-depth conversion and seismic velocity estimation using time-migration velocity |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Inversion Methods
Previous: Finite difference method
Alternatively, we solve our PDE
in the form given by equation 15
by a spectral Chebyshev method Boyd (2001).
Using cubic splines, we define the input data at 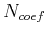 Chebyshev points.
We compute the Chebyshev coefficients and the coefficients of the
derivatives in the right-hand side of equation 15.
Then we use a smaller number
Chebyshev points.
We compute the Chebyshev coefficients and the coefficients of the
derivatives in the right-hand side of equation 15.
Then we use a smaller number  of the
coefficients for function evaluation.
We need to do such Chebyshev differentiation twice.
Finally we perform the time step using
the stable third-order Adams-Bashforth method
Boyd (2001),
which is
of the
coefficients for function evaluation.
We need to do such Chebyshev differentiation twice.
Finally we perform the time step using
the stable third-order Adams-Bashforth method
Boyd (2001),
which is
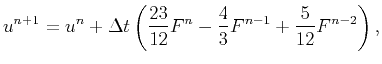 |
(23) |
where
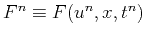 is the right-hand side.
In numerical examples, we tried
is the right-hand side.
In numerical examples, we tried
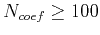 and
and
 .
This method allows larger time steps than the finite difference, and
has the adjustable parameter
.
This method allows larger time steps than the finite difference, and
has the adjustable parameter  .
.
For step 2, we use a Dijkstra-like solver introduced in Cameron et al. (2007).
It is an efficient time-to-depth conversion algorithm motivated by
the Fast Marching Method (Sethian, 1996).
The input for this algorithm
is
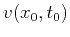 and the outputs are
the seismic velocity
and the outputs are
the seismic velocity 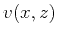 and the transition matrices from time-domain
to depth-domain coordinates
and the transition matrices from time-domain
to depth-domain coordinates 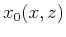 and
and 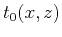 . We solve the
eikonal equation with an unknown right-hand side coupled
with the orthogonality relation
. We solve the
eikonal equation with an unknown right-hand side coupled
with the orthogonality relation
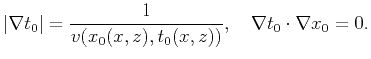 |
(24) |
The orthogonality relation means that the image rays are orthogonal to
the wavefronts. Such time-to-depth conversion is very fast and
produces the outputs directly on the depth-domain grid.
 |
 |
 |
 | Time-to-depth conversion and seismic velocity estimation using time-migration velocity |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Inversion Methods
Previous: Finite difference method
2013-07-26
![]() and the outputs are
the seismic velocity
and the outputs are
the seismic velocity ![]() and the transition matrices from time-domain
to depth-domain coordinates
and the transition matrices from time-domain
to depth-domain coordinates ![]() and
and ![]() . We solve the
eikonal equation with an unknown right-hand side coupled
with the orthogonality relation
. We solve the
eikonal equation with an unknown right-hand side coupled
with the orthogonality relation