Next: About this document ... Up: Chen: Deblending using SVMF Previous: Bibliography

Appendix: Review of local similarity

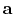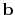Fomel (2007) defined local similarity between vectors $\mathbf{a}$ and $\mathbf{b}$ as:

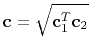$\displaystyle \mathbf{c}=\sqrt{\mathbf{c}_1^T\mathbf{c}_2}$

(7)

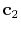where $\mathbf{c}_1$ and $\mathbf{c}_2$ come from two least-squares minimization problem:

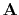$\displaystyle \mathbf{c}_1$	$\displaystyle =\arg\min_{\mathbf{c}_1}\Arrowvert \mathbf{A}-\mathbf{C}_1 \mathbf{B} \Arrowvert_2^2$	(8)
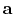$\displaystyle \mathbf{c}_2$	$\displaystyle =\arg\min_{\mathbf{c}_2}\Arrowvert \mathbf{B}-\mathbf{C}_2 \mathbf{A} \Arrowvert_2^2$	(9)

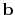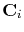where $\mathbf{A}$ is a diagonal operator composed from the elements of $\mathbf{a}$ , $\mathbf{B}$ is a diagonal operator composed from the elements of $\mathbf{b}$ , and $\mathbf{C}_i$ is a diagonal operator composed from the elements of $\mathbf{c}_i$ . LS problems A-2 and A-3 can be solved with the help of shaping regularization with a local-smoothness constraint:

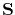$\displaystyle \mathbf{c}_1$	$\displaystyle = [\lambda_1^2\mathbf{I} + \mathbf{S}(\mathbf{B}^T\mathbf{B}-\lambda_1^2\mathbf{I})]^{-1}\mathbf{SB}^T\mathbf{a},$	(10)
$\displaystyle \mathbf{c}_2$	$\displaystyle = [\lambda_2^2\mathbf{I} + \mathbf{S}(\mathbf{A}^T\mathbf{A}-\lambda_2^2\mathbf{I})]^{-1}\mathbf{SA}^T\mathbf{b},$	(11)

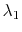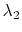where $\mathbf{S}$ is a smoothing operator and $\lambda_1$ and $\lambda_2$ are two parameters controlling the physical dimensionality and enabling fast convergence when inversion is implemented iteratively. These two parameters can be chosen as 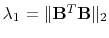$\lambda_1 = \Arrowvert\mathbf{B}^T\mathbf{B}\Arrowvert_2$ and $\lambda_2 = \Arrowvert\mathbf{A}^T\mathbf{A}\Arrowvert_2$ .

Next: About this document ... Up: Chen: Deblending using SVMF Previous: Bibliography

2015-11-23