 |
 |
 |
 | Stacking angle-domain common-image gathers for normalization of illumination |  |
![[pdf]](icons/pdf.png) |
Next: STACKING USING LOCAL SIMILARITY
Up: Liu et al.: Stacking
Previous: ANGLE-DOMAIN COMMON-IMAGE GATHERS
Fomel (2007a) defined the local similarity attribute using shaping regularization (Fomel, 2007b). The global correlation coefficient between two discrete signals 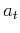 and
and 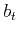 is defined as
is defined as
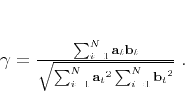 |
(2) |
To locally measure correlation between two signals according to the definition of local similarity (Fomel, 2007a; Fomel and Long, 2009), local similarity 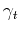 can be represented as the product of two least-squares inverses:
can be represented as the product of two least-squares inverses:
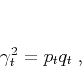 |
(3) |
![\begin{displaymath}
p_t = \arg \,\,\,\, \min_{p_t} \left(\sum_{t}\left(a_t-p_tb_t\right)^2+R\left[p_t\right]\right)\;,
\end{displaymath}](img13.png) |
(4) |
![\begin{displaymath}
q_t = \arg \,\,\,\, \min_{q_t} \left(\sum_{t}\left(a_t-q_tb_t\right)^2+R\left[q_t\right]\right)\;,
\end{displaymath}](img14.png) |
(5) |
where 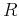 is a regularization operator designed to constrain the solution in a desired behavior, such as smoothness. Shaping regularization (Fomel, 2007b) can conveniently be applied in solving inverse problems (4) and (5) iteratively. The local similarity can smoothly measure the correlation between two signals locally. It is an estimate of waveform similarity of two seismic signals.
is a regularization operator designed to constrain the solution in a desired behavior, such as smoothness. Shaping regularization (Fomel, 2007b) can conveniently be applied in solving inverse problems (4) and (5) iteratively. The local similarity can smoothly measure the correlation between two signals locally. It is an estimate of waveform similarity of two seismic signals.
 |
 |
 |
 | Stacking angle-domain common-image gathers for normalization of illumination |  |
![[pdf]](icons/pdf.png) |
Next: STACKING USING LOCAL SIMILARITY
Up: Liu et al.: Stacking
Previous: ANGLE-DOMAIN COMMON-IMAGE GATHERS
2013-07-26
![]() and
and ![]() is defined as
is defined as