Field data example

I first use a 2D field data example to compare the difference between K-SVD and SGK methods, as shown in Figure 4. The data size of this example is $512\times 512$ . In this example, I choose a patch size of $8\times8$. The overlap between different patches is $7$ points in both vertical and horizontal directions. Thus the atom size $M=8\times8=64$, and the number of sample signals is thus $N=(512-7)\times(512-7)=255025$. The size of $\mathbf{D}$ is $64\times255025$. For K-SVD, the dictionary updating process takes about 1590.2s, while for SGK, the dictionary updating process takes only 87.23s, which shows a great speedup. Figure 5a shows the initial input dictionary. Figures 5b and 5c show the learned dictionaries using K-SVD and SGK, respectively. The two learned dictionaries show some similarities but are not exactly the same. As can be seen in either Figure 5b or 5c that there are some atoms in the middle part of the dictionary map containing linear patterns, indicating a better representation of the locally linear events. In this example, I also compare the K-SVD and SGK methods with two other widely known methods, i.e. the DDTF method (Cai et al., 2013) and the seislet transform method (Fomel and Liu, 2010). The denoised results using four methods are shown in Figure 6. The corresponding noise sections are shown in Figure 7. Comparing the results in both Figures 6 and 7, I can roughly get some conclusions that K-SVD, SGK, and DDTF methods all seem to obtain successful denoised results while the result from seislet transform is a bit over-smoothed, which causes some observable low-frequency coherent energy in the noise section (Figure 7d). A better evaluation of denoising performance can be obtained using the local similarity measurement and is shown in Figure 8. The local similarity confirms my observation in that the local similarity corresponding to seislet method is very high, which is followed by the DDTF method. The DDTF method obtains a successful performance in most part of the data but causes some damages to the highly curved signals around the 2s near the left boundary, as indicated from the local similarity map (Figure 8c). The K-SVD and SGK methods obtain very close results but SGK results in a slightly higher local similarity in right part of the data.

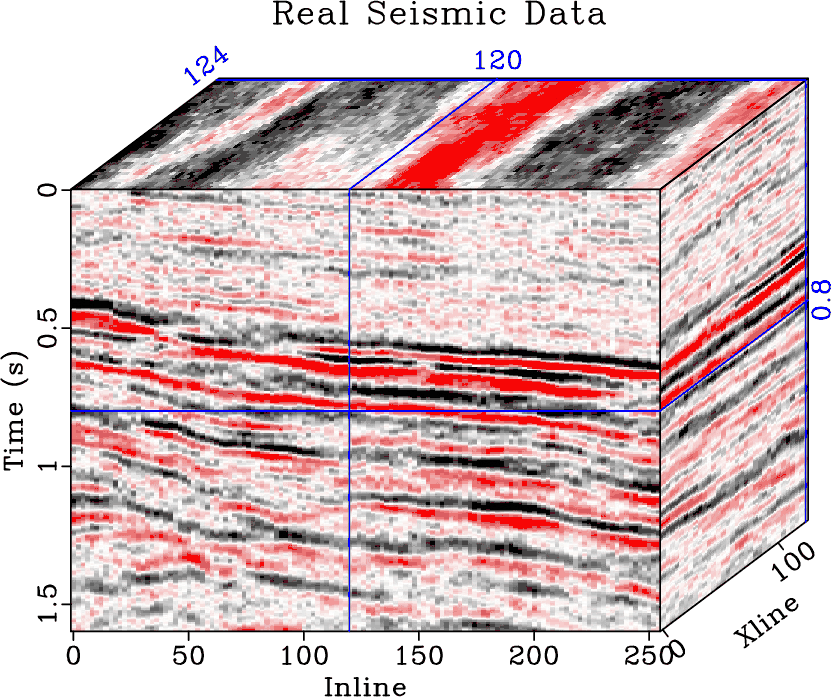
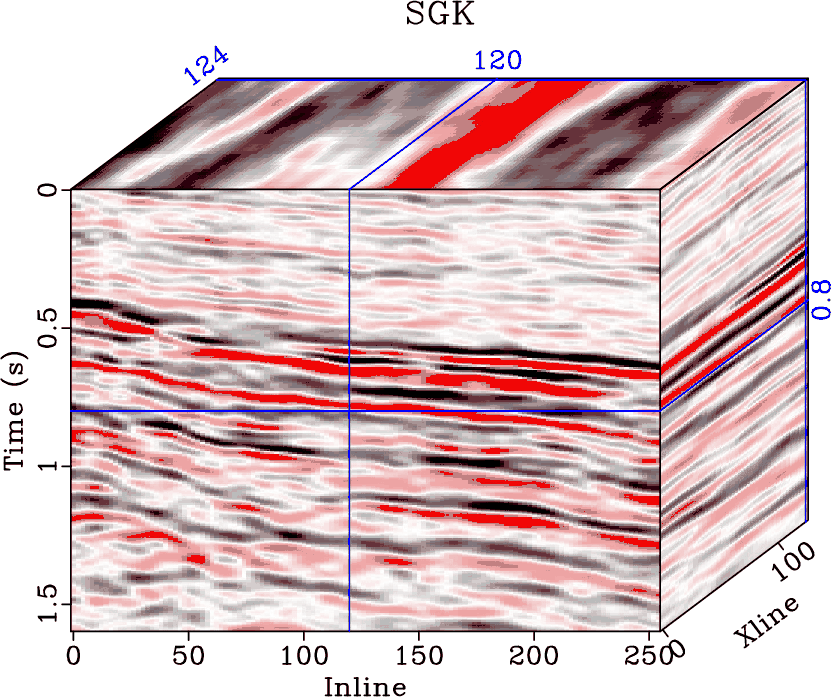
I next use a 3D field data example to demonstrate the performance, as shown in Figure 9. Figures 9a, 9b, and 9c show noisy data, K-SVD denoised data and SGK denoised data, respectively. Figures 9d and 9e show the noise sections of two approaches. It is clear that both approaches obtain approximate performance. It is computationally expensive to use K-SVD to learn the dictionary for this example. While it takes about half an hour to learn the dictionary using SGK algorithm, it takes more than half a day to learn the dictionary using the K-SVD algorithm. The local similarity cubes between denoised data cubes and removed noise cubes using two methods are shown in Figure 10, which confirms the successful and comparable performance of both methods in that most part of the data is close to zero.

field2d
Figure 4. Noisy 2D field data.

dicfield0,dicfieldksvd,dicfieldsgk
Figure 5. (a) Initial overcomplete DCT dictionary. (b) Learned dictionaries using K-SVD. (c) Learned dictionaries using SGK. Each atom in the dictionary has been reshaped into a 2D matrix. As can be seen in either (b) or (c) that there are some atoms in the middle part of the dictionary map containing linear patterns, indicating a better representation of the locally linear events.

field2d-ksvd,field2d-sgk,field2d-ddtf,field2d-seis
Figure 6. (a) Denoised data using K-SVD. (b) Denoised data using SGK. (c) Denoised data using DDTF. (d) Denoised data using seislet thresholding.

field2d-n-ksvd,field2d-n-sgk,field2d-n-ddtf,field2d-n-seis
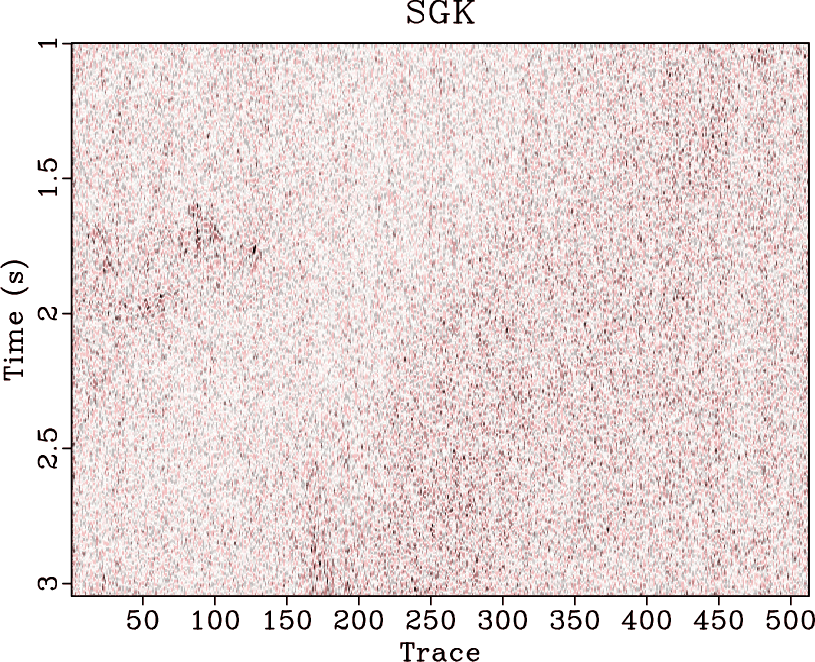
Figure 7. (a) Removed noise using K-SVD. (b) Removed noise using SGK. (c) Removed noise using DDTF. (d) Removed noise using seislet thresholding.

field2d-simi1,field2d-simi2,field2d-simi3,field2d-simi4
Figure 8. Local similarity between denoised data and removed noise using (a) K-SVD, (b) SGK, (c) DDTF and (d) seislet thresholding.

field3d,field3d-ksvd,field3d-sgk,field3d-ksvd-n,field3d-sgk-n
Figure 9. (a) Noisy 3D field data. (b) & (c) Denoised data using K-SVD and SGK. (d) & (e) Noise cubes using K-SVD and SGK.

field3d-simi1,field3d-simi2
Figure 10. (a) Local similarity between denoised data using K-SVD and the corresponding noise cube. (b) Local similarity between denoised data using SGK and the corresponding noise cube.