A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations

Global vector distributions

The goal of this subsection is to determine an appropriate scheme for distributing global vectors, i.e., ones representing a function over the entire domain (as opposed to only over a panel). And while the factorizations themselves may have occurred on subteams of $O(p/m)$ processes each, in order to make use of all available processes for every subdomain solve, at this point we assume that each auxiliary problem's frontal tree has been selectively inverted and is distributed using a subtree-to-subteam mapping (recall Fig. 4) over the entire set of $p$ processes.

Since a subtree-to-subteam mapping will assign each supernode of an auxiliary problem to a team of processes, and each panel of the original 3D domain is by construction a subset of the domain of an auxiliary problem, it is straightforward to extend the supernodal subteam assignments to the full domain. We should then be able to distribute global vectors so that no communication is required for readying panel subvectors for subdomain solves (via extension by zero for interior panels, and trivially for the first panel). Since our nested dissection process does not partition in the shallow dimension of quasi-2D subdomains (see Fig. 3), extending a vector defined over a panel of the original domain onto the PML-padded auxiliary domain simply requires individually extending each supernodal subvector by zero in the $x_3$ direction.

Consider an element-wise two-dimensional cyclic distribution (30) of a frontal matrix $F$ over $q$ processes using an $r \times c$ process grid, where $r$ and $c$ are $O(\sqrt{q})$ . Then the $(i,j)$ entry will be stored by the process in the $(i \bmod r,j \bmod c)$ position in the process grid. Using the notation from (30), this distributed front would be denoted as $F[M_C,M_R]$ , while its top-left quadrant would be referred to as $F_{TL}[M_C,M_R]$ (see Fig. 5 for a depiction of an $[M_C,M_R]$ matrix distribution).

Figure 5: Overlay of the owning process ranks of an 7 $\times$ 7 matrix distributed over a 2 $\times$ 3 process grid in the $[M_C,M_R]$ distribution, where $M_C$ assigns row $i$ to process row $i \bmod 2$ , and $M_R$ assigns column $j$ to process column $i \bmod 3$ (left). The process grid is shown on the right.

Loosely speaking, $F[X,Y]$ means that each column of $F$ is distributed using the scheme denoted by $X$ , and each row is distributed using the scheme denoted by $Y$ . For the element-wise two-dimensional distribution used for $F$ , $[M_C,M_R]$ , we have that the columns of $F$ are distributed like Matrix Columns ($M_C$ ), and the rows of $F$ are distributed like Matrix Rows ($M_R$ ). While this notation may seem vapid when only working with a single distributed matrix, it is useful when working with products of distributed matrices. For instance, if a `$\star$ ' is used to represent rows/columns being redundantly stored (i.e., not distributed), then the result of every process multiplying its local submatrix of $A[X,\star]$ with its local submatrix of $B[\star,Y]$ forms a distributed matrix $C[X,Y] = (AB)[X,Y] = A[X,\star]\, B[\star,Y]$ , where the last expression refers to the local multiplication process.

We can now decide on a distribution for each supernodal subvector, say $x_{\mathcal{S}}$ , based on the criteria that it should be fast to form $F_{TL} x_{\mathcal{S}}$ and $F_{TL}^T x_{\mathcal{S}}$ in the same distribution as $x_{\mathcal{S}}$ , given that $F_{TL}$ is distributed as $F_{TL}[M_C,M_R]$ . Suppose that we define a Column-major Vector distribution ($V_C$ ) of $x_{\mathcal{S}}$ , say $x_{\mathcal{S}}[V_C,\star]$ , to mean that entry $i$ is owned by process $i \bmod q$ , which corresponds to position $(i \bmod r,\lfloor i/r \rfloor \bmod c)$ in the process grid (if the grid is constructed with a column-major ordering of the process ranks; see the left side of Fig. 6). 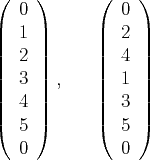Then a call to MPI_Allgather (10) within each row of the process grid would allow for each process to collect all of the data necessary to form $x_{\mathcal{S}}[M_C,\star]$ , as for any process row index $s \in \{0,1,...,r-1\}$ ,

$$\{ i \in \mathbb{N}_0 : i \bmod r = s \} = \bigcup_{t=0}^{c-1} \{ i \in \mathbb{N}_0 : i \bmod q = s+tr \}.$$ (7)

See the left side of Fig. 7 for an example of an $[M_C,\star ]$ distribution of a $7 \times 3$ matrix.

Figure 6: Overlay of the owning process ranks of a vector of height 7 distributed over a 2 $\times$ 3 process grid in the $[V_C,\star ]$ vector distribution (left) and the $[V_R,\star ]$ vector distribution (right).

Figure 7: Overlay of the owning process ranks of a vector of height 7 distributed over a 2 $\times$ 3 process grid in the $[M_C,\star ]$ distribution (left) and the $[M_R,\star ]$ distribution (right).

Similarly, if $x_{\mathcal{S}}$ was distributed with a Row-major Vector distribution ($V_R$ ), as shown on the right side of Fig. 6, say $x_{\mathcal{S}}[V_R,\star]$ , so that entry $i$ is owned by the process in position $(\lfloor i/c \rfloor \bmod r,i \bmod c)$ of the process grid, then a call to MPI_Allgather within each column of the process grid would provide each process with the data necessary to form $x_{\mathcal{S}}[M_R,\star]$ . Under reasonable assumptions, both of these redistributions can be shown to have per-process communication volume lower bounds of $\Omega(n/\sqrt{p})$ (if $F_{TL}$ is $n \times n$ ) and latency lower bounds of $\Omega(\log_2(\sqrt{p}))$  (9). We also note that translating between $x_{\mathcal{S}}[V_C,\star]$ and $x_{\mathcal{S}}[V_R,\star]$ simply requires permuting which process owns each local subvector, so the communication volume would be $O(n/p)$ , while the latency cost is $O(1)$ .

We have thus described efficient techniques for redistributing $x_{\mathcal{S}}[V_C,\star]$ to both the $x_{\mathcal{S}}[M_R,\star]$ and $x_{\mathcal{S}}[M_C,\star]$ distributions, which are the first steps for our parallel algorithms for forming $F_{TL} x_{\mathcal{S}}$ and $F_{TL}^T x_{\mathcal{S}}$ , respectively: Denoting the distributed result of each process in process column $t \in \{0,1,...,c-1\}$ multiplying its local submatrix of $F_{TL}[M_C,M_R]$ by its local subvector of $x_{\mathcal{S}}[M_R,\star]$ as $z^{(t)}[M_C,\star]$ , it holds that $(F_{TL} x_{\mathcal{S}})[M_C,\star] = \sum_{t=0}^{c-1} z^{(t)}[M_C,\star]$ . Since Eq. (7) also implies that each process's local data from a $[V_C,\star ]$ distribution is a subset of its local data from a $[M_C,\star ]$ distribution, a simultaneous summation and scattering of $\{z^{(t)}[M_C,\star]\}_{t=0}^{c-1}$ within process rows, perhaps via MPI_Reduce_scatter or MPI_Reduce_scatter_block, yields the desired result, $(F_{TL} x_{\mathcal{S}})[V_C,\star]$ . An analogous process with $(F_{TL}[M_C,M_R])^T=F_{TL}^T[M_R,M_C]$ and $x_{\mathcal{S}}[M_C,\star]$ yields $(F_{TL}^T x_{\mathcal{S}})[V_R,\star]$ , which can then be cheaply permuted to form $(F_{TL}^T x_{\mathcal{S}})[V_C,\star]$ . Both calls to MPI_Reduce_scatter_block can be shown to have the same communication lower bounds as the previously discussed MPI_Allgather calls (9).

As discussed at the beginning of this section, defining the distribution of each supernodal subvector specifies a distribution for a global vector, say $[\mathcal{G},\star]$ . While the $[V_C,\star ]$ distribution shown in the left half of Fig. 6 simply assigns entry $i$ of a supernodal subvector $x_{\mathcal{S}}$ , distributed over $q$ processes, to process $i \bmod q$ , we can instead choose an alignment parameter, $\sigma$ , where $0 \le \sigma < q$ , and assign entry $i$ to process $(i + \sigma) \bmod q$ . If we simply set $\sigma=0$ for every supernode, as the discussion at the beginning of this subsection implied, then at most $O(\gamma n)$ processes will store data for the root separator supernodes of a global vector, as each root separator only has $O(\gamma n)$ degrees of freedom by construction. However, there are $m=O(n/\gamma)$ root separators, so we can easily allow for up to $O(n^2)$ processes to share the storage of a global vector if the alignments are carefully chosen. It is important to notice that the top-left quadrants of the frontal matrices for the root separators can each be distributed over $O(\gamma^2 n^2)$ processes, so $O(\gamma^2 n^2)$ processes can actively participate in the corresponding triangular matrix-vector multiplications.

A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations