 |
 |
 |
 | A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations |  |
![[pdf]](icons/pdf.png) |
Next: Parallel sweeping preconditioner
Up: Introduction
Previous: Moving PML sweeping preconditioner
A domain decomposition variant of the sweeping preconditioner was recently
introduced (37) which results in fast convergence rates,
albeit at the expense of requiring PML padding on both sides of each subdomain.
Recalling our previous analysis with respect to the PML size,
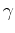 , the memory usage of the preconditioner scales linearly with the
PML size, while the setup cost scales quadratically. Thus, the domain
decomposition approach should be expected to use twice as much memory and
require four times as much work for the setup phase.
On the other hand, doubling the subdomain sizes allows for more parallelism
in both the setup and solve phases, and less sweeps seem to be required.
, the memory usage of the preconditioner scales linearly with the
PML size, while the setup cost scales quadratically. Thus, the domain
decomposition approach should be expected to use twice as much memory and
require four times as much work for the setup phase.
On the other hand, doubling the subdomain sizes allows for more parallelism
in both the setup and solve phases, and less sweeps seem to be required.
Another closely related method is the
Analytic ILU factorization (19).
Like the sweeping preconditioner, it uses local approximations of the Schur
complements of the block  factorization of the Helmholtz matrix
represented in block tridiagonal form.
There are two crucial differences between the two methods:
factorization of the Helmholtz matrix
represented in block tridiagonal form.
There are two crucial differences between the two methods:
- Roughly speaking, AILU can be viewed as using Absorbing Boundary
Conditions (ABC's) (13) instead of PML when forming
approximate subdomain auxiliary problems.
While ABC's result in strictly 2D local subproblems,
versus the quasi-2D subdomain problems which result from using PML,
they are well-known to be less effective approximations of the Sommerfeld
radiation condition (and thus the local Schur complement approximations
are less effective). The sweeping preconditioner handles its non-trivial
subdomain factorizations via a multifrontal algorithm.
- Rather than preconditioning with an approximate
 factorization
of the original Helmholtz operator, the sweeping preconditioner sets up
an approximate factorization of a slightly damped Helmholtz operator
in order to mitigate the dispersion error which would result from the
Schur complement approximations.
factorization
of the original Helmholtz operator, the sweeping preconditioner sets up
an approximate factorization of a slightly damped Helmholtz operator
in order to mitigate the dispersion error which would result from the
Schur complement approximations.
These two improvements are responsible for transitioning from the 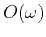 iterations required with AILU to the
iterations required with AILU to the  iterations needed with the
sweeping preconditioner (for problems without large cavities).
iterations needed with the
sweeping preconditioner (for problems without large cavities).
Two other iterative methods warrant mentioning: the two-grid shifted-Laplacian
approach of (8) and the multilevel-ILU approach of
(6). Though both require 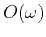 iterations
for convergence, they have very modest memory requirements.
In particular, (8) demonstrates that, with a properly
tuned two-grid approach, large-scale heterogeneous 3D problems can be solved
with impressive timings.
iterations
for convergence, they have very modest memory requirements.
In particular, (8) demonstrates that, with a properly
tuned two-grid approach, large-scale heterogeneous 3D problems can be solved
with impressive timings.
There has also been a recent effort to extend the fast-direct methods presented
in (43) from definite elliptic problems into the realm of
low-to-moderate frequency time-harmonic wave
equations (40,41).
In particular, their experiments (see Table 3 of (40)) suggest an
asymptotic complexity of roughly
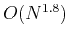 , which is a noticeable improvement
over the
, which is a noticeable improvement
over the 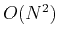 complexity of traditional 3D sparse-direct methods.
complexity of traditional 3D sparse-direct methods.
 |
 |
 |
 | A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations |  |
![[pdf]](icons/pdf.png) |
Next: Parallel sweeping preconditioner
Up: Introduction
Previous: Moving PML sweeping preconditioner
2014-08-20
![]() factorization of the Helmholtz matrix
represented in block tridiagonal form.
There are two crucial differences between the two methods:
factorization of the Helmholtz matrix
represented in block tridiagonal form.
There are two crucial differences between the two methods:
![]() iterations
for convergence, they have very modest memory requirements.
In particular, (8) demonstrates that, with a properly
tuned two-grid approach, large-scale heterogeneous 3D problems can be solved
with impressive timings.
iterations
for convergence, they have very modest memory requirements.
In particular, (8) demonstrates that, with a properly
tuned two-grid approach, large-scale heterogeneous 3D problems can be solved
with impressive timings.
![]() , which is a noticeable improvement
over the
, which is a noticeable improvement
over the ![]() complexity of traditional 3D sparse-direct methods.
complexity of traditional 3D sparse-direct methods.