 |
 |
 |
 | Velocity-independent time-domain seismic imaging
using
local event slopes |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Fomel: Seismic imaging using
Previous: Conclusions
I would like to thank Jon Claerbout and Antoine Guitton for inspiring
discussions. Huub Douma, Gilles Lambaré, Isabelle Lecomte,
and one anonymous reviewer provided thorough and helpful reviews.
This publication is authorized by the Director, Bureau of Economic
Geology, The University of Texas at Austin.
Appendix
A
Mathematical derivation of oriented Dix inversion
The famous Dix inversion formula (Dix, 1955) can be
written in the form
![\begin{displaymath}
v_i^2 = \frac{d}{d\,t_0}\,\left[t_0\,v^2(t_0)\right]\;,
\end{displaymath}](img63.png) |
(21) |
where  is the interval velocity corresponding to the zero-offset
traveltime
is the interval velocity corresponding to the zero-offset
traveltime  and
and  is the vertically-variable
root-mean-square velocity. By a straightforward application of the
chain rule, I rewrite the Dix equation in the form
is the vertically-variable
root-mean-square velocity. By a straightforward application of the
chain rule, I rewrite the Dix equation in the form
![\begin{displaymath}
v_i^2 = \frac{d\,\left[t_0(t)\,v^2(t)\right]/d\,t}
{d\,t_0/d\,t}.
\end{displaymath}](img64.png) |
(22) |
Substituting  and
and 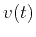 dependences from
equations 3 and 4 and doing algebraic
simplifications yields
dependences from
equations 3 and 4 and doing algebraic
simplifications yields
where
 . Substituting
equations A-3 and A-4 into A-2
produces equation 15 in the main text.
. Substituting
equations A-3 and A-4 into A-2
produces equation 15 in the main text.
Appendix
B
Mathematical derivation of oriented time-domain imaging operators

|
|---|
rays
Figure B-1. Reflection ray geometry in an
effectively homogeneous medium (a scheme).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
The mathematical derivation of oriented time-domain imaging operators
follows geometrical principles. Consider the
reflection ray geometry in Figure B-1. Making a hyperbolic
approximation of diffraction traveltimes used in seismic time
migration is equivalent to assuming an effective constant-velocity
medium and straight-ray geometry. The geometrical connection between
the effective dip angle  , the effective reflection
angle
, the effective reflection
angle  , the effective velocity
, the effective velocity  , half-offset
, half-offset  , and the
reflection traveltime
, and the
reflection traveltime  is given by the equation
is given by the equation
 |
(25) |
which follows directly from the trigonometry of the reflection
triangle (Fomel, 2003b; Clayton, 1978). Additionally,
the two angles are connected with the traveltime derivatives
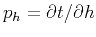 and
and
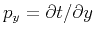 according to
equations
according to
equations
Using equations B-1, B-2, and B-3, one
can explicitly solve for the effective parameters  ,
,  ,
and
,
and  expressing them in terms of the data coordinates
expressing them in terms of the data coordinates  and
and  and
event slopes
and
event slopes 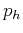 and
and  . The solution takes the form
. The solution takes the form
Note that equation B-6 is equivalent to
equation 20 in the main text. It reduces to
equation 4 in the case of a horizontal reflector (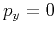 ).
).
With the help of equations B-4, B-5,
and B-6, one can transform all other geometrical quantities
associated with time-domain imaging into data attributes. The vertical
two-way time is (Sava and Fomel, 2003)
 |
(31) |
which turns, after substituting equations B-4
and B-5, into equation 18 in the main
text. The separation between the midpoint and the vertical is
(Sava and Fomel, 2003)
 |
(32) |
which turns, after substituting equations B-4
and B-5, into equation 19 in the main text.
Additionally, the zero-offset traveltime is (using equation B-7)
 |
(33) |
which turns into equation 16. Finally, the separation
between the midpoint and the zero-offset point is (using
equations B-1 and B-8)
 |
(34) |
which turns into equation 17. In the case of a horizontal
reflector (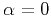 ),
),  ,
,  , and the zero-offset
traveltime reduces to the NMO-corrected traveltime in
equation 3.
, and the zero-offset
traveltime reduces to the NMO-corrected traveltime in
equation 3.
Non-hyperbolic and three-dimensional generalizations of this theory are
possible.
 |
 |
 |
 | Velocity-independent time-domain seismic imaging
using
local event slopes |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Fomel: Seismic imaging using
Previous: Conclusions
2013-07-26

![]() , the effective reflection
angle
, the effective reflection
angle ![]() , the effective velocity
, the effective velocity ![]() , half-offset
, half-offset ![]() , and the
reflection traveltime
, and the
reflection traveltime ![]() is given by the equation
is given by the equation